Название: Реализация и анализ ЦФ с КИХ

Вид работы: курсовая работа

Рубрика: Коммуникации и связь

Размер файла: 209.78 Kb

Скачать файл: referat.me-167688.docx

Краткое описание работы: Цифровой согласованный фильтр с конечной импульсной характеристикой. Импульсная характеристика согласованного фильтра. Входной аналоговый и дискретизированный ЛЧМ сигналы. Нормированный отклик фильтра на заданный сигнал. Амплитудный спектр фильтра.

Реализация и анализ ЦФ с КИХ

Министерство общего и профессионального образования

Российской Федерации

УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕОРЕТИЧЕСКИХ ОСНОВ РАДИОТЕХНИКИ

реализация и анализ цф с ких

Курсовая работа

Руководитель

Коберниченко В.Г.

Студент

Литвинов А.А.

Группа Р-33072

Екатеринбург 2006 г.

1. Задание

Разработать цифровой согласованный фильтр (СФ) с конечной импульсной характеристикой и получить следующие его характеристики:

- спектр входного сигнала;

- спектральную (амплитудно-частотную) характеристику окна;

- АЧХ и ИХ фильтра;

- отклик фильтра на заданный сигнал;

- спектр выходного сигнала.

Проанализировать полученные результаты.

Параметры фильтра (Вариант №16):

Тип фильтра: согласованный с заданным сигналом фильтр;

Тип окна: Ханна;

Тип сигнала: прямоугольный радиоимпульс с несущей частотой, равной f_д /4, и внутриимпульсной ЛЧМ (девиация частоты равна f_д /4, база сигнала равна 30, скважность – 15).

2. Расчет фильтра

ПРИМЕЧАНИЕ: Все машинные расчеты в данном задании будут проводиться в среде MatLabv 6.5.

Так как в данном задании используется сигнал с B=20, воспользуемся формулами для ЛЧМ-сигналов с большой базой:

, где =dw – частота девиации, а = dw/ti– скорость нарастания частоты импульса.

Аналоговый сигнал имеет вид: при и 0 при .

Импульсная характеристика согласованного фильтра описывается выражением , где k – коэффициент, зависящий от физической реализации устройства (алгоритма), реализующего СФ. Для простоты анализа в дальнейшем амплитуду сигнала включим в k, и приравняем его к 1.

Далее нужно рассчитать, сколько точек необходимо для реализации согласованного фильтра. Сначала сосчитаем, сколько точек нужно для реализации радиоимпульса длиной t_и .: . Для заданного сигнала

Тогда fд выберем равной 120 Гц, а f0, равную fd/4 – соответственно 30 Гц. В этом случае максимальная частота импульса составит f0+df = 0.25Fd+0.25fd, т.е, ровно половину от частоты дискретизации: 60 Гц, следовательно теорема Котельникова будет выполнена и наложения спектров не наступит. Длительность аналогового импульса равна 1с, дискретного – 120 отсчетов (точек).

Дискретизированный сигнал имеет вид:

U_дискр (n) = U_аналог (n*T_д ):

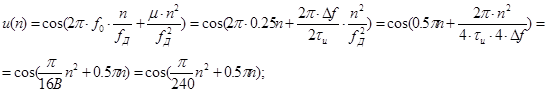
n = 0..N_и -1 = 0..119;

Далее построим выражение для импульсной характеристики фильтра:

Особенностью согласованного фильтра является то, что его импульсная характеристика h(t) является зеркальным отображением сигнала S(t) относительно прямой t=t₀ /2 (рис.1).

Рисунок 1

Это справедливо и для цифрового согласованного фильтра, поэтому:

Дискретная ИХ СФ:

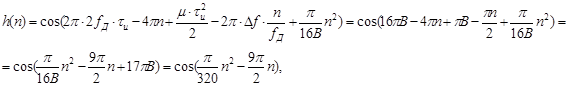
n=0..N_и -1=0..119;

так как функция cos(t) - 2p-периодическая. В MatLabже зеркальное отражение можно осуществить, если инвертировать массив отсчетов дискретизированного импульса, причем n нужно брать не от 0 до N_и -1, а от 1 до N_и , что обусловлено тем, что нумерация элементов в массивах в MatLаb ведется, начиная с единицы.

Полученная импульсная характеристика затем взвешивается окном Ханна:

w(n) = 0.5(1-cos(2π*(n-1)/(N_и -1))) на интервале причем данное окно необходимо сдвинуть вправо на , чтобы перекрывать весь сигнал. В MatLab это окно (уже со сдвигом) строится функцией hann(N_и ).

На выходе согласованного фильтра после появления на входе сигнала, с которым он согласован, в момент окончания сигнала t_и должна появиться автокорреляционная функция(АКФ) этого сигнала. Аппроксимирующее выражение для нормированной АКФ ЛЧМ сигнала имеет вид:

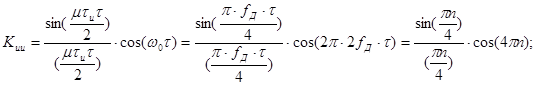
В дальнейшем для определенности, амплитуду и дискретного и наналогового сигнала я беру равной 1.

Теперь приведу необходимые графики(для расчетов использована программа MatLAB):

1) Входной аналоговый и дискретизированный ЛЧМ сигналы S(t) и S(n):

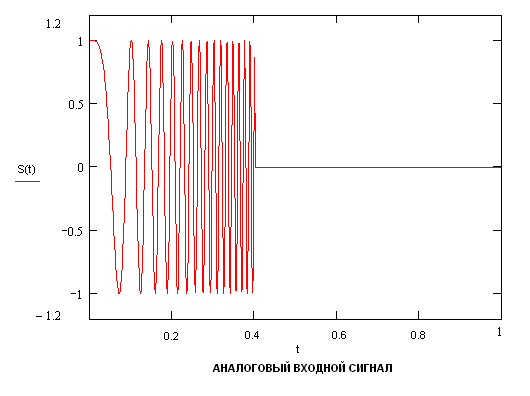
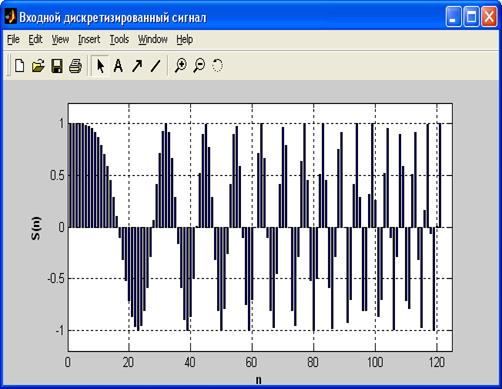
2) Амплитудный спектр (АЧХ) входного сигнала Ws(n):

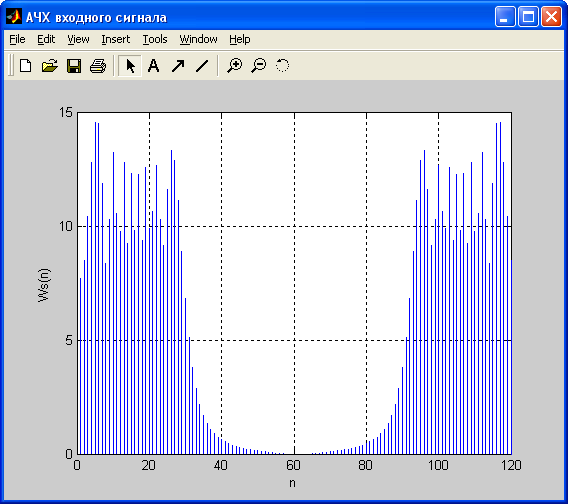
3) Вид и АЧХокна:

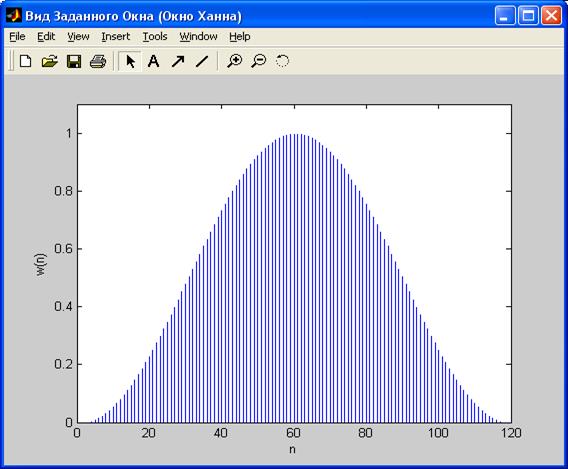
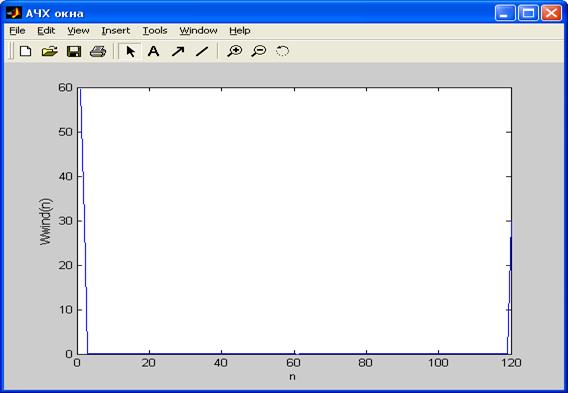
4) ИХ взвешенного фильтра:

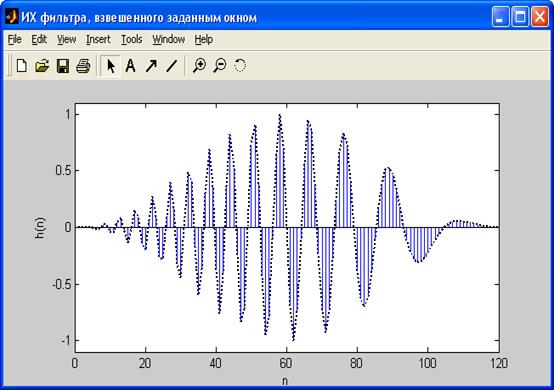
5) АЧХ взвешенного фильтра:

6) Спектр выходного сигнала (подвергшегося согласованной фильтрации). Получается перемножением спектров входного сигнала и спектра взвешенного фильтра:

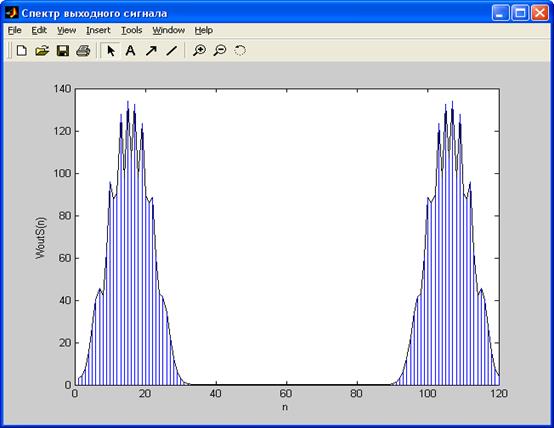
7) Нормированный отклик фильтра на заданный сигнал – Kssf(tau) /tau – величина сдвига/. Отклик получен сверткой входного сигнала и ИХ взвешенного окном фильтра:

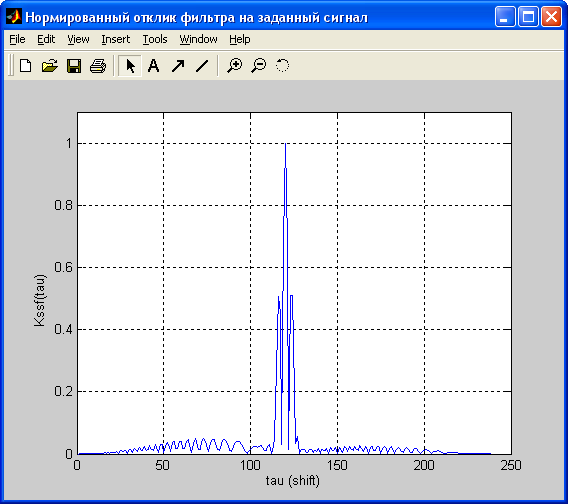
Теперь сравним полученный отклик с аппроксимацией АКФ входгого сигнала (см. следующую страницу):

8) Смещенная на Nи АКФ входного сигнала (отклик СФ без окна на входной сигнал) Kss(tau) /tau – величина сдвига/. Отклик получен сверткой входного сигнала и ИХ ещё не взвешенного окном СФ:

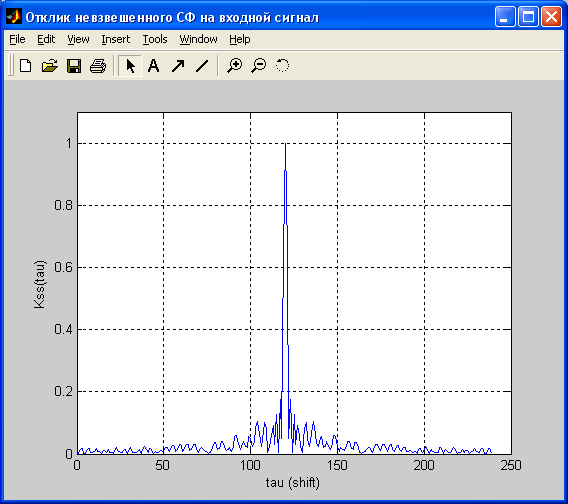
ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

В ходе выполнения настоящего домашнего задания был реализован согласованный фильтр с конечной импульсной характеристикой (КИХ – фильтр).

Коэффициенты этого КИХ-фильтра – это отсчеты его импульсной характеристики, полученной в ходе вычислений. Кроме теоретического алгоритма, приведенного мной в начале задания, разработан непосредственно машинный алгоритм реализации заданного фильтра для выполнения в среде MatLab 6.5.

Листинг программы (с комментариями автора):

i=1; % инициализация программного счетчика

Ni=120; % задание количества отсчётов импульса

h=[1:Ni]; % подготовка массива отсчетов ИХ к последующему заполнению

ti=120; % задание длины импульса в точках

Fd=120; % задание частоты дискретизации

F0=Fd/4; %задание несущей частоты

Wd=2*pi*Fd; % задание угловой частоты дискретизации

W0=2*pi*F0; %задание угловой несущей частоты

dF=Fd/4; % задание девиации частоты

dW=dF*2*pi; % задание угловой девиации частоты

mju=dF/ti; % задание скорости роста частоты (скорость частотной модуляции)

n=0:1/Fd:1-1/Fd; % подготовка дискретов времени с шагом, равным периоду дискретизации

Sn=chirp(n,0,1,dF); % заполнение массива отсчетов дискретизированного сигнала

figure(1)

bar(Sn,0.1); % вывод на экран графика входного сигнала

f=abs(fft(Sn,Ni)); % вычисление спектра входного сигнала с использованием БПФ

figure(2);

stem(f); % постоение графика спектра входного сигнала

w=hann(Ni); % вычисление Ni-точечного окна Ханна

figure(3);

stem(w); % построение графика вычисленного окна

Ww=abs(fft(w,Ni)); % вычисление амплитудного спектра вычисленного окна с помощью БПФ

figure(4);

plot(Ww); % построени найденного спектра

while i<=Ni, % цикл нахождения ИХ СФ (путем зеркального отражения входного сигнала)

h(i)=Sn(Ni-i+1);

i=i+1;

end

hw=h.*w'; % взвешивание фильтра окном полученным окном Ханна

stem(hw); % построение графика ИХ взвешенного фильтра

Whw=abs(fft(hw)); % вычисление АЧХ взвешенного фильтра с пом. алгоритма БПФ

stem(Whw); % построение графика найденного амплитудного спектра взвешенного фильтра

WoutS=f.*Whw; % перемножение АЧХ сигнала и СФ для вычисления АЧХ сигнала на выходе

plot(WoutS); % построение графика найденной АЧХ выходного сигнала

respnormw=conv(Sn,hw); % получение отклика СФ на заданный сигнал

respnorm=conv(Sn,h); % получение отклика невзвешенного СФ на входной сигнал

figure(5);

plot(abs(respnormw/max(respnormw))); % построение графика отклика СФ на заданный сигнал

figure(6);

plot(abs(respnorm/max(respnorm))); % вывод графика отклика невзвешенного СФ на входной %сигнал

ВЫВОДЫ

В ходе выполнения настоящей курсовой работы был реализован согласованный фильтр с конечной импульсной характеристикой (КИХ-фильтр) методом окна (Ханна), получены его коэффициенты, импульсная и амплитудно – частотная хпрактеристики. Получены отклики реализованного СФ на входной сигнал во взвешенном и в начальном состоянии и построены их наглядные графики, что позволяет провести анализ синтезированного фильтра.

Из проведенного анализа полученного фильтра следует, что фильтр построен правильно, так как отклик фильтра имеет более широкий главный лепесток, чем аппроксимация АКФ (отклик этого же фильтра в невзвешенном состоянии), причем боковые лепестки за счет этого подавлены. Задание выполнено, так как коэффициенты фильтра получены.