Название: Окремі випадки задач оптимального стохастичного керування

Вид работы: реферат

Рубрика: Коммуникации и связь

Размер файла: 389.3 Kb

Скачать файл: referat.me-167920.docx

Краткое описание работы: 1. Зовнішній інтеграл Функції можуть бути довільними, а математичні сподівання можна обчислювати, якщо як функція від є вимірною. Якщо ж оптимальна стратегія, отримана в результаті оптимізації, виявиться невимірною, то і функція

Окремі випадки задач оптимального стохастичного керування

ОКРЕМІ ВИПАДКИ ЗАДАЧ ОПТИМАЛЬНОГО СТОХАСТИЧНОГО КЕРУВАННЯ

1.Зовнішній інтеграл

Функції і можуть бути довільними, а математичні сподівання можна обчислювати, якщо як функція від є вимірною.

Якщо ж оптимальна стратегія, отримана в результаті оптимізації, виявиться невимірною, то і функція може виявитися невимірною. У цьому випадку математичне сподівання невизначено.

Для розв’язання цієї проблеми застосовують два підходи. Перший полягає в накладенні на функції і таких обмежень, які забезпечували б вимірність підінтегральної функції на кожному кроці оптимізації : функції і , , повинні бути неперервними по своїх аргументах і повинна існувати щільність імовірності розподілу випадкової величини , а множини значень припустимих стратегій повинні бути компактними.

На жаль, на практиці ці вимоги не завжди виконуються. Тому другий підхід пов’язаний з використанням зовнішнього інтеграла.

Позначимо через простір елементарних подій, що є довільною множиною, а – деяка система підмножин множини .

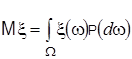Математичним сподіванням випадкової величини , заданої на імовірнісному просторі , називається число , якщо інтеграл з правої частини існує.

Нехай і – борелівські простори, , є -алгеброю в . Функція називається -вимірною, якщо для будь-якої множини . Тут – борелівська -алгебра простору .

Для функції , () зовнішній інтеграл за мірою визначається як нижня грань інтегралів від всіх вимірних функцій (), що мажорують , тобто

, .

Тут – функція розподілу випадкової величини , що відповідає ймовірнісній мірі .

Для довільної функції має місце співвідношення:

,

де , , і вважають, що .

Оскільки зовнішній інтеграл визначений для будь-якої функції, як для вимірної, так і для невимірної, то ніяких додаткових обмежень на функції і накладати не треба.

Для вимірних функцій обидва види математичних сподівань співпадають. Отже, у постановках задач можна замінити звичайне математичне сподівання на зовнішнє, і навіть якщо знайдена при цьому функція виявиться вимірною, то отримана стратегія керування не перестане бути оптимальною.

Зовнішня міра множини визначається співвідношенням .

Для будь-якої множини

,

де – це індикатор множини , що визначається як

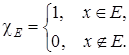
а) якщо , то ;

б) якщо і , то ;

в) якщо або , то ;

г) якщо задовольняє рівності , то для будь-якої функції має місце рівність ;

д) якщо , то для будь-якої функції ;

е) якщо і , то . Якщо при цьому хоча б одна з функцій або -вимірна, то останнє співвідношення вірно зі знаком рівності.

Позначимо через дійсну пряму, а через – розширену дійсну пряму і надалі у всіх висновках замість дійсної прямої використовуватимемо поняття розширеної дійсної прямої.

Вважатимемо, що для розширеної дійсної прямої мають місце всі співвідношення порядку додавання і множення, які було введено для , і припустимо, що і .

Позначимо через множину всіх дійсних у розширеному розумінні функцій , де – простір станів.

– банахів простір всіх обмежених дійсних функцій з нормою, що визначається за формулою

, .

Позначатимемо , якщо , , і , якщо , , .

Для будь-якої функції і будь-якого числа позначимо через функцію, що приймає значення в кожній точці , так, що

, .

Припущення монотонності. Для будь-яких станів , керування і функцій мають місце нерівності

якщо і ;

, якщо і ;

, якщо , і .

Для будь-якого стратегія називається -оптимальною при горизонті , якщо

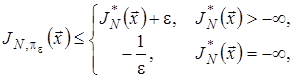
і -оптимальною, якщо

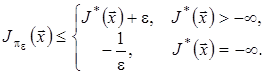
Багато задач послідовної оптимізації, що становлять практичний інтерес, можуть розглядатися як окремі випадки задач загального виду. Розглянемо деякі з них:

· задачі детермінованого оптимального керування;

· задачі стохастичного керування зі зліченним простором збурень;

· задачі стохастичного керування із зовнішнім інтегралом;

· задачі стохастичного керування з мультиплікативним функціоналом витрат;

· задачі мінімаксного стохастичного керування.

2. Детерміноване оптимальне керування

Розглянемо відображення , що задане формулою

, , , (1)

за таких припущень:

функції і відображають множину відповідно в множини і , тобто , ; скаляр додатний.

За цих умов відображення задовольняє припущенню монотонності. Якщо функція дорівнює нулю, тобто , , то відповідна -крокова задача оптимізації (1) набуває вигляду:

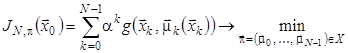, (2)

. (3)

Ця задача є задачею детермінованого оптимального керування зі скінченним горизонтом. Задача з нескінченним горизонтом має наступний вигляд:

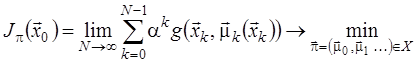, (4)

. (5)

Границя в (4) існує, якщо має місце хоча б одна з наступних умов:

· , , ;

· , , ;

· , , , і деякого .

У задачі (4) – (5) може бути уведене додаткове обмеження на стан системи , . У такому разі, якщо , позначатимемо .

3. Оптимальне стохастичне керування: зліченний простір збурень

Розглянемо відображення , що задане формулою

, (6)

за таких припущень:

параметр приймає значення зі зліченної множини з заданим розподілом ймовірностей , що залежать від і ; функції і відображають множину відповідно в множини і , тобто , ; скаляр додатний.

Якщо , , – елементи множини , – довільний розподіл ймовірностей на , а – деяка функція, то математичне сподівання визначається за формулою

,

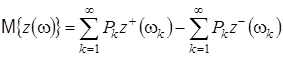де ,

,

.

Оскільки , то математичне сподівання визначене для будь-якої функції і будь-якого розподілу ймовірностей на множині .

Зокрема, якщо , ,… – розподіл ймовірностей на множині , то формулу (6) можна переписати так:

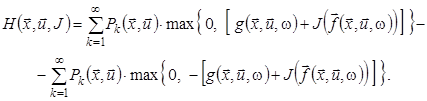
При використанні цього співвідношення треба пам’ятати, що для двох функцій , рівність має місце, якщо виконується хоча б одна з трьох умов:

та ;

та ;

та .

Відображення задовольняє припущенню монотонності. Якщо функція – тотожний нуль, тобто , , то за умови , , функцію витрат за кроків можна подати у вигляді:

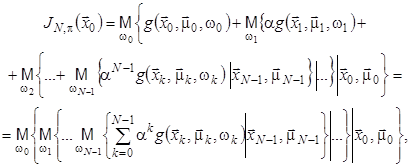(7)

де , .

Ця умова означає, що математичне сподівання обчислюється послідовно по всіх випадкових величинах .

При цьому зміна порядку операцій додавання і узяття математичного сподівання припустима, тому що , , і для довільних простору з мірою , вимірної функції і числа має місце рівність .

Якщо виконується одна з двох нерівностей

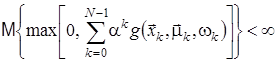або

,

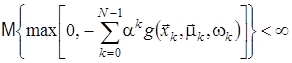то функцію витрат за кроків можна записати у вигляді:

,

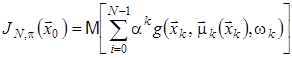де математичне сподівання обчислюється на добутку мір на , а стани , , виражаються через за допомогою рівняння .

Якщо функція допускає подання у такому вигляді для будь-якого початкового стану та будь-якої стратегії , то -крокова задача може бути сформульована так:

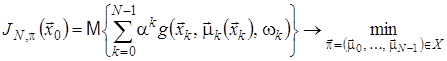, (8)

. (9)

Відповідна задача з нескінченним горизонтом формулюється так:

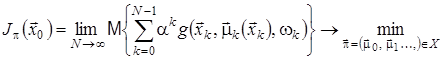, (10)

. (11)

Границя в (10) існує при виконанні будь-якої з трьох наступних умов:

· , , , ;

· , , , ;

· , , , , і деякого .

Математичне сподівання визначається і як звичайний інтеграл, і як зовнішній інтеграл з -алгеброю в множині , що складається із всіх підмножин , в залежності від вимірності або невимірності функцій.

Для багатьох практичних задач виконується припущення про зліченність множини .

Якщо ж множина незліченна, то справа ускладнюється необхідністю обчислення математичного сподівання

для будь-якої функції . Подолання цих труднощів і пов’язане з використанням зовнішнього інтеграла.