Название: Форма напряжения на выходе дифференцирующей, интегрирующей и распределительной RC-цепи

Вид работы: контрольная работа

Рубрика: Коммуникации и связь

Размер файла: 516.92 Kb

Скачать файл: referat.me-168221.docx

Краткое описание работы: Воздействие одиночного прямоугольного импульса на вход интегрирующей цепи. Определение изменения напряжения на емкости в момент времени. Число реактивных элементов (индуктивностей, емкостей). Комплексная передаточная функция напряжения интегрирующей цепи.

Форма напряжения на выходе дифференцирующей, интегрирующей и распределительной RC-цепи

Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Контрольная работа по курсу

"Основы радиоэлектроники и схемотехники"

2009

Задание 1, задача 1

Решение:

Цепь представленная на рис.1 является интегрирующей, если постоянная времени цепи t=RC будет удовлетворять условию:

t>>tи

На практике цепь считается интегрирующей, если t= (5…10) tи

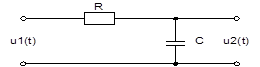
Рисунок 1

Согласно заданию на вход интегрирующей цепи воздействует одиночный прямоугольный импульс, описываемый следующим уравнением:

u1 (t) = 10, при 0≤t<10^-6

0, при t≥10^-6

Поскольку выходное напряжение интегрирующей цепи u2 (t) равно напряжению на конденсаторе C uc (t), то для определения формы выходного напряжения необходимо определить изменения напряжения на конденсаторе. Форма выходного напряжения может быть найдена как алгебраическая сумма откликов на положительный и отрицательный скачки.1. Определим изменение напряжения на емкости в момент времени 0≤t<tи, где tи - длительность импульса равная 1 мкс.

В соответствии с классическим методом расчета, переходное напряжение представляют в виде суммы принужденного и свободного напряжений.

u (t) = u_пр (t) +u_св (t) ( 1)

где u_пр (t) - принужденное напряжение, определяется в установившемся режиме после коммутации. Это напряжение создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденное напряжение будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный напряжение изменяется по периодическому, синусоидальному закону;

u_св (t) - свободное напряжение, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободное напряжение создается внутренними источниками питания например зарядом емкости.

Свободное напряжение u_св (t) определяется по формуле

u_св (t) =A1e^p1t +A2e^p2t +….

Количество слагаемых в формуле определяется числом реактивных элементов (индуктивностей и емкостей)где A1, A2 - постоянные интегрирования.p1, p2 - корни характеристического уравнения.

Уравнение 1+pRC=0 называется характеристическим

p=-1/RC - корень характеристического уравнения

t=1/p=RC - постоянная времени цепи

Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю.Исходя из вышесказанного формулу (1) можно записать в следующем виде:uc (t) = uc_пр +Ae^pt = uc_пр +Ae-^{t/ t} ( 2) В начальный момент времени емкость не заряжена и uc (0) =0

uc (0) = uc_пр +A

A=uc (0) - uc_пр =0 - uc_пр = - uc_пр =-E ( 3)

На основании формул (1) и (2) переходное напряжение на емкости в момент времени 0≤t<tи будет определятся по формуле:

uc (t) = E-Ee-^{t/ t} =E (1-e^{-t/ t} ) ( 4)

2. Определим изменение напряжения на емкости в момент времени t≥tи.

В данный момент времени импульс на входе цепи равен 0 и емкость начинает разряжаться, что эквивалентно существованию в цепи только свободного напряжения, принужденное напряжение равно нулю. Напряжение на емкости за длительность импульса tи достигнет напряжения равного:

uc (0) =A=uc_св (0) =E-Ee^-tи/τ

Тогда в соответствии с формулой (1) и с учетом того что принужденное напряжение равно нулю имеем переходное напряжение на емкости в момент времени t≥tи:

uc (t) = uc_св (t) =Ae^-t/τ = (E-Ee^-tи/τ ) e^{-t/ τ} =E (e^{-t/ τ} -e^{- (t+tи) /τ} ) ( 5)

Подставив в формулы (4) и (5) значения заданного сигнала E=10В, tи=1мкс, а также τ =5tи =5мкс и просуммировав переходные напряжения на емкости в разные моменты времени получим отклик интегрирующей цепи на входной прямоугольный импульс:

u2 (t) = 10 × (1-e^-t/0.000005 ) при 0≤t<10^-6

10 × (e^-t/0.000005 -e^{- (t+0.000001) /0.000005} ) при t≥10^-6

На рисунке 2 приведены графики u1 (t) и u2 (t)

интегрирующая распределительная цепь напряжение

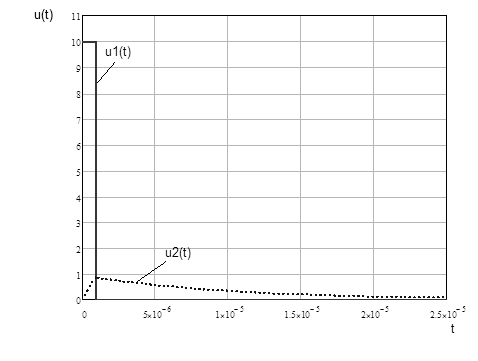
Рисунок 2

Комплексная передаточная функция напряжения интегрирующей цепи равна:

.

Тогда амплитудно-частотная и фазово-частотная характеристики примут вид:

.

Графики амплитудно-частотной и фазово-частотной характеристик для заданной интегрирующей цепи приведем на рисунках 3 и 4 соответственно.

Ширина полосы пропускания интегрирующей RC - цепи равна частоте среза

w_ср =1/t=1/5×10^-6 =2×10⁵

f_ср =w_ср /2p=3,183×10⁴ Гц

Рисунок 3

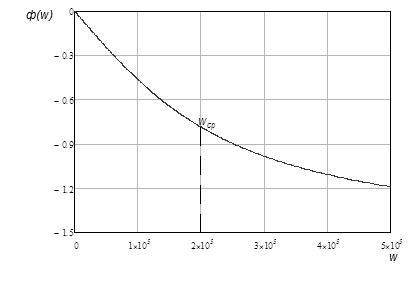
Рисунок 4

Пусть на вход этой же интегрирующей цепи воздействуют периодические прямоугольные импульсы с частотой 100 кГц, длительностью tи = 1 мкс.

Определим отклик интегрирующей цепи на данное воздействие спектральным методом. Для этого произведем разложение периодической последовательности импульсов в ряд Фурье в вещественной форме. Ограничим количество гармонических сигналов в ряде 15-ю, что позволит получить сигнал с довольно высокой точностью.

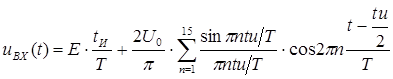
Амплитудно-частотная и фазо-частотная характеристики цепи имеют вид:

Отклик на выходе цепи будет представлять собой произведение каждой гармоники входного сигнала на частотный коэффициент передачи цепи на соответствующей частоте:

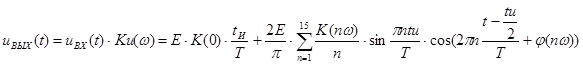
С учетом равенств:

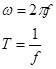
Построим временные диаграммы u_вх (t) и u_вых (t) при помощи пакета MathCAD.

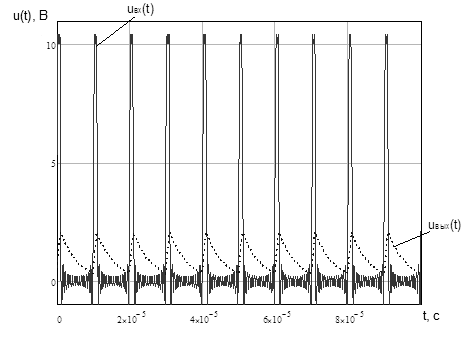
Задание 1, Задача 5

Большое применение находит аналитический метод анализа, получивший название метода угла отсечки. Угол отсечки, числено равен половине той части периода, в течение которого через НЭ протекает ток.

Угол отсечки легко найти из равенства :

(1)

Угол отсечки, соответствующий максимуму n-ой гармоники в спектре тока (при ) определяется по формуле:

Выразив в формуле (1) u₀ получаем смещение при котором на выходе НЭ первая гармоника тока будет максимальной.

Функция тока определяется следующим выражением:

. (2)

При :

Амплитуды спектральных составляющих тока через НЭ определяются через коэффициенты Берга:

(3)

где коэффициенты являются функциями одного аргумента - угла отсечки , получили название коэффициентов (функций) Берга.

Функции Берга можно определить по следующим формулам

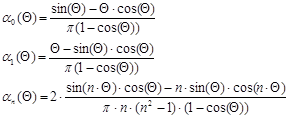
Значения функций Берга для угла отсечки равного 180⁰ сведем в таблицу 1

Таблица 1

a0	a1	a2	a3	a4
0,5	0,5	0	0	0

Согласно формуле (3) спектральные составляющие тока равны:

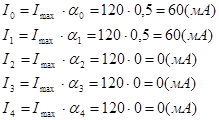
Коэффициент гармоник определим по формуле:

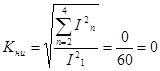
Эпюры входного сигнала и тока протекающего через НЭ приведем на рисунке 1.

Рисунок 1

Задание 2, Задача 1

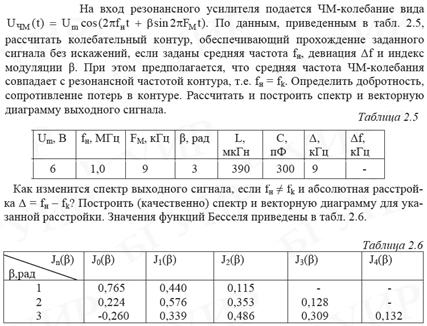
Определим девиацию частоты по следующей формуле:

(1)

Спектр частотно модулированного сигнала при наличии одной модулирующей частоты определяется по формуле:

(2)

где J₀ (b), J₁ (b), J₂ (b), J₃ (b), J₄ (b) - функции Бесселя;

w_н - несущая частота равная 2pf_н ;

w_М - модулирующая частота равная 2pF_М .

Подставив значения в формулу (2) имеем:

Спектр ЧМ-сигнала имеет вид представленный на рисунке 1.

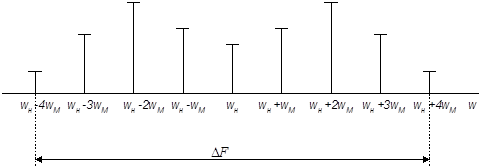
Рисунок 1

Исходя из найденного спектра и определив максимальную частоту отстройки от несущей частоты

Исходя из вышесказанного полоса ЧМ-сигнала будет равна удвоенному значению максимальной частоты отстройки

Для того чтобы ЧМ сигнал не искажался контуром резонансного усилителя необходимо чтобы полоса пропускания контура была не менее полосы ЧМ сигнала. Добротность колебательного контура и полоса пропускания контура связаны следующим соотношением:

(3)

где f_k - резонансная частота контура равная 1 МГц;

- полоса пропускания контура 72 кГц

Тогда добротность контура равна:

С другой стороны добротность контура можно выразить через характеристическое сопротивление контура r сопротивление потерь в контуре R:

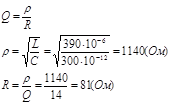
Качественно спектр ЧМ сигнала с контуром настроенным на несущую частоту и расстроенным относительно несущей частоты на D представлены на рисунке 2.

Рисунок 2

Расстройка выходного контура относительно несущей частоты и при абсолютной расстройке D равной 9 кГц приведет к тому, что гармоника ЧМ сигнала с частотой f_н +4F_М не попадет в полосу пропускания контура и будет подавлена, что приведет к искажению ЧМ сигнала.

Определим характер сопротивления цепи при абсолютной расстройке на 9 кГц. Для этого определим относительную расстройку по формуле:

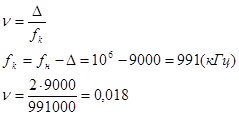
Определим обобщенную расстройку

Определим сопротивление контура при резонансе и при расстройке

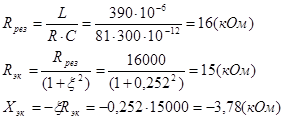
Полное сопротивление при расстройке равно:

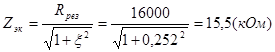
Определим фазу контура при расстройке:

Поскольку фаза имеет отрицательное значение, то ток при расстройке опережает напряжение.

При резонансе ток и напряжения совпадают по фазе. Векторные диаграммы токов и напряжений при резонансе и расстройке приведены на рисунке 3.

Рисунок 3

Задание 3, задача 3

Решение:

Входные и выходные характеристики транзистора КТ608А представлены на рисунках 1 и 2 соответственно

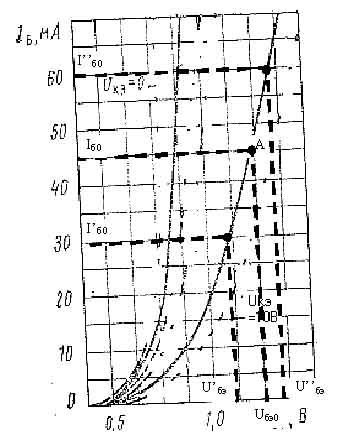
Рисунок 1

I’k

Ik 0

I’’k

Iiv k

I’’’k

U’кэ

U’’ кэ

Uкэ0

A

I’’б0

I’б0

Iб0

I’k

Ik 0

I’’k

Iiv k

I’’’k

U’кэ

U’’ кэ

Uкэ0

A

I’’б0

I’б0

Iб0

Рисунок 2

Рассмотрим методику определения h-параметров БТ по статическим ВАХ.

Статические ВАХ БТ позволяют определить дифференциальные параметры транзистора. Для описания свойств транзистора по переменному току чаще всего используется система дифференциальных h-параметров, которая представляется следующими уравнениями:

dU₁ = h₁₁ dI₁ + h₁₂ dU₂ ;

dI₂ = h₂₁ dI₁ + h₂₂ dU₂ .

Для нахождения h-параметров по статическим характеристикам дифференциалы заменим конечными приращениями и получим выражения, позволяющие определить физический смысл h-параметров

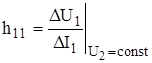- входное сопротивление в режиме короткого замыкания (КЗ) на выходе;

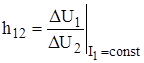- коэффициент обратной связи по напряжению в режиме холостого хода (ХХ) по входу;

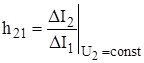- коэффициент передачи по току в режиме КЗ на выходе;

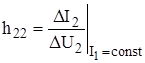- выходная проводимость в режиме ХХ по входу.

Для расчета h-параметров удобно использовать семейства входных и выходных характеристик БТ. Рассмотрим порядок графо-аналитического метода расчета h-параметров БТ с ОЭ. Для определения дифференциальных параметров и в заданной рабочей точке А (, , ) на линейном участке семейства входных характеристик необходимо выполнить построения, как показано на рис.1. Найденные приращения токов и напряжений позволяют определить искомые параметры:

,

.

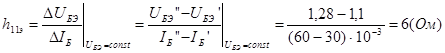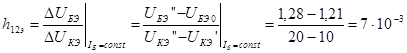Параметры и определяются по семейству выходных характеристик. В окрестности точки А' (, , ), соответствующей точке А на семействе входных характеристик, выполняют построения как показано на рис.2. Найденные приращения токов и напряжений позволяют определить искомые параметры:

,

.

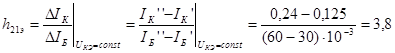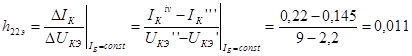Значения приращений входного и выходного напряжения должны выбираться таким образом, чтобы вспомогательные точки на графиках находились на их линейных участках.

Физическая Т-образная эквивалентная схема транзистора со структурой n-p-n, представленная на рис 3, достаточно полно отражает свойства реального транзистора на низких частотах и используется при анализе транзисторных схем. Значения параметров эквивалентной схемы БТ могут быть найдены с использованием известных h-параметров

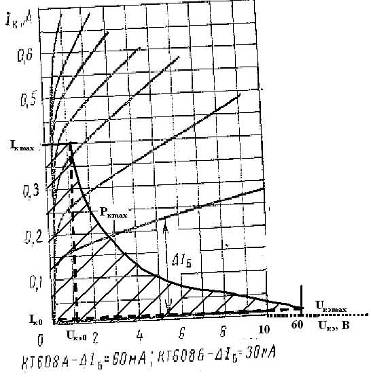
Рисунок 3

,

,

,

.

На выходных характеристиках транзистора определим допустимую область работы Iк max = 400 мА, Pкmax = 0,5 Вт, Uкэmax = 60 В

При Iкmax = 0,4 А, Uкэ0 = Pкmax/Iкmax = 0.5/0.4 = 1.25 В

При Uкэmax = 60 В Iк0 = Pкmax/Uкэmax = 0,5/ 60 = 8 мА

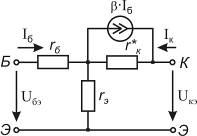
Рисунок 4