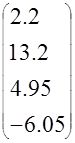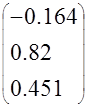Название: Расчет цифрового корректора
Вид работы: контрольная работа
Рубрика: Коммуникации и связь
Размер файла: 165.88 Kb
Скачать файл: referat.me-170605.docx
Краткое описание работы: Контрольная работа студентов-заочников по дисциплине «Цифровая обработка сигналов» Расчет цифрового корректора Задан канал передачи дискретных сообщений. Межсигнальная
Расчет цифрового корректора
![]()
Контрольная работа
студентов-заочников по дисциплине
«Цифровая обработка сигналов»
Расчет цифрового корректора
Задан канал передачи дискретных сообщений. Межсигнальная
интерференция сигналов в канале определяется импульсной характеристикой, отсчеты которой равны:
g0![]() g(0)=(-1)
g(0)=(-1)![]() *(m+1)/20
*(m+1)/20
g1![]()
![]() g(t)=1
g(t)=1
g2![]() g(2T)=(-1)
g(2T)=(-1)![]() *(n+1)/20
*(n+1)/20
где m-предпоследняя цифра № зачетной книжки
n-последняя цифра №зачетной книжки
1.Используя выражение дискретной свертки, рассчитать сигнал на выходе канала в отсчетные моменты 0,1,2,3 для последовательности входных сигналов u(0),u(T)
a) u(0)=U, u(T)=0
Где U=n+1
b) u(0)=U, u(T)=U
В другие отсчетные моменты u(2T)=u(3T)=0
2.Рассчитать коэффициенты цифрового корректора C![]() ,C
,C![]() ,C
,C![]() ,обеспечивающие выходной сигнал “010” при подаче на
,обеспечивающие выходной сигнал “010” при подаче на
вход канала сигнала “100”.
3.Рассчитать сигналы на выходе корректора при входных сигналах (a),(b).Проанализировать эффективность работы корректора.
Пример выполнения для m=3,n=10
Отсчеты импульсной характеристики равны
g0=0.2; g1=1; g2= -0.5; U=11
![]()
![]() Задание 1
Задание 1
Пусть u1(kT)-сигал на выходе канала связи (входе корректора)
В соответствии с выражением дискретной свертки он равен
u1(kT)=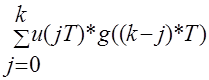 k=0,1,2,3
k=0,1,2,3
Учитывая,что u(jT)=0 для j![]() 1 и g(mT)=0 для m
1 и g(mT)=0 для m![]() 2, получаем
2, получаем
k=0 u1(0)=u(0)*g(0)=u(0)*g0
k=1 u1(T)=u(0)*g(T)+u(T)*g(0)=u(0)*g1+u(T)*g0
k=2 u1(2T)=u(0)*g(2T)+u(T)*g(T)=u(0)*g2+u(T)*g1
k=3 u1(3T)=u(T)*g(2T)=u(T)*g2
Для варианта (а) u(0)=11,u(T)=0
u1(0)=11*0.2=2.2 u1(T)=11*1+0*0.2=11 u1(2T)=11*(-0.55)+0*1=-6.05 u1(3T)0*(-0.55)=0 |
U1=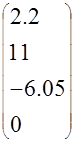 |
Для варианта (б) u(0)=11,u(T)=11
u1(0)=11*0.2=2.2 u1(T)=11*1+11*0.2=13.2 u1(2T)=11*(-0.55)+11*1=4.95 u1(3T)=11*(-0.55)=-6.05 |
U1= |
Задание 2(пояснение)

| t |
0 T 2T
![]() g g1
g g1
![]() 2T
2T
T |
0 T g2
| g1 | g0 | 0 |
| g2 | g1 | g0 |
| g2 | g1 |
![]()
![]()
![]()
![]()
![]() C
C![]()
![]()
![]() С
С![]()
![]()
![]() С
С![]()
![]()
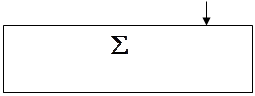 |
![]()
![]()
система из 3-х уравнений Матрица коэф- Вектор Вектор
с 3-мя неизвестными фициентов неизвестного прав.
коэффициента частей
корректора
![]()
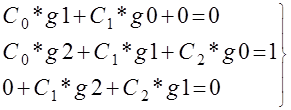 G=
G=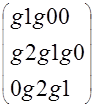
![]() C=
C=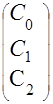 H=
H=![]()
![]()
В векторно-матричной форме G*C=H
 *
*![]() =
=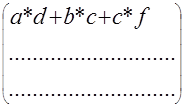
Умножаем слева на обратную матрицу G![]()
![]()
G![]() *G*C= G
*G*C= G![]() *H,откуда С= G
*H,откуда С= G![]() *H,где
*H,где
Умножаем слева на обратную матрицу G![]()
![]()
G![]() *G*C= G
*G*C= G![]() *H, откуда С= G
*H, откуда С= G![]() *H,где
*H,где
(G![]() *G)-единичная матрица
*G)-единичная матрица ![]()
![]()
Решение с помощью системы Mathcad
|
|
|
Введите
Задайте матрицу G:=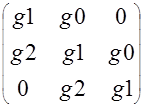 |
Вектор H:= |
||||
Вычислите C:=G |
Рассчитайте |
Решение системы уравнений по формуле Крамера
С![]() =D
=D![]() /D
/D![]() C
C![]() =D
=D![]() /DC
/DC![]() =D
=D![]() /D
/D
где D- определитель матрицы G
D=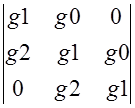 =
=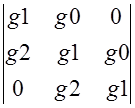
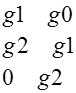 =g1
=g1![]() -g2*g0*g1-g1*g2*g0=
-g2*g0*g1-g1*g2*g0=
=1-2*g0*g2=1-2*0.2*(-0.55)=1.22
D=1.22
D![]() -определитель матрицы G,где 1-й столбец заменен на вектор H
-определитель матрицы G,где 1-й столбец заменен на вектор H
D![]() =
=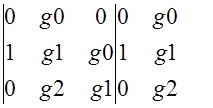 =0-g1*1*g0=-g0=-0.2
=0-g1*1*g0=-g0=-0.2
D![]() -определьтель матрицы G ,где 2-й столбец заменен на H
-определьтель матрицы G ,где 2-й столбец заменен на H
D![]() =
=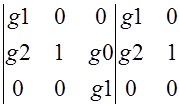 =g1
=g1![]() -0=1
-0=1
D![]() -определитель матрицы G,где 3-й столбец заменен на H
-определитель матрицы G,где 3-й столбец заменен на H
D![]() =
=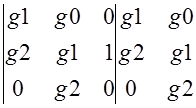 =0-g2*1*g1=0.55
=0-g2*1*g1=0.55
Таким образом, коэффициенты Вектор коэффициентов
корректора равны
С C C |
С=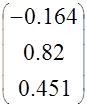 |
|||||
Задание 3 Прохождение сигнала U1(kT) через корректор иллюстрируется схемой: |
||||||
U1(kT |
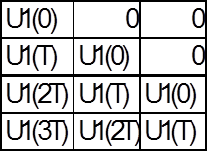 |
V(0)=U1(0)*C V(T)=U1(T)*C V(2T)=U1(2T)*C V(2T)=U1(3T)*C |
||||
![]() C
C![]()
![]()
![]() С
С![]()
![]()
![]()
![]()
![]()
![]() С
С![]()
![]()
V(kT) |
V(0)=2.2*(-0.164)=-0.361 V(T)=11*(-0.164)+2.2*0.82=0 V(2T)=(-0.6.05)* (-0.164)=11*0.82+2.2*0.451=11.004 V(3T)=0*(-0.164)+ (-6.05)*0.82+11*0.451 |
Вектор выходного сигнала
![]()
![]()
![]()
![]() (а) Ожидаемый (б) Ожидаемый
(а) Ожидаемый (б) Ожидаемый
сигнал сигнал
V=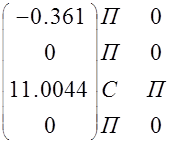
![]() V=
V=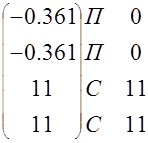
Максимальный модуль разности между ожидаемым и полученным выходным сигналом
(а) (б)
![]()
![]()
![]()
![]() V
V![]() =0,361 V
=0,361 V![]() =0.361
=0.361
![]()
![]()
![]()
![]()
![]()
![]() V
V![]()
![]() 0 V
0 V![]()
![]() 0
0
На выходе корректора:
![]()
![]()
![]()
![]() (а) ожидаемый (б) ожидаемый
(а) ожидаемый (б) ожидаемый
сигнал сигнал
![]()
![]()
![]()
![]()
![]()
![]() U1=
U1=![]()
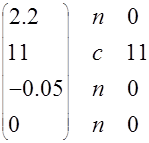 U1=
U1=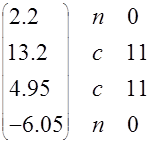
![]()
![]() U1
U1![]() =6.05 U1
=6.05 U1![]() =6.05
=6.05
![]() U1
U1![]() =0 U1
=0 U1![]() =6.05
=6.05
Сопоставление максимальных погрешностей до коррекции и после коррекции:
![]() (а) (б)
(а) (б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() U1
U1![]()
![]() V1
V1![]() U1
U1![]() V1
V1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() U1
U1![]() = V1
= V1![]() U1
U1![]() V1
V1![]()
свидетельствует об эффективной работе корректора.
Похожие работы
-
Технология приборостроения
Министерство образования Российской Федерации Казанский государственный технический университет филиал «Восток» кафедра приборостроения КУРСОВОЙ ПРОЕКТ
-
Коррекция частотных искажений сигналов
Основное требование безискаженной передачи сигналов: функция группового времени задержки должна быть частотно независимой величиной. Физические свойства усилителей, фильтров и проводных линий. Причины возникновения амплитудных и фазо-частотных искажений.
-
Контрольная по телетрафику
Министерство высшего и профессионального образования РФ Ижевский Государственный Технический Университет Приборостроительный факультет Контрольная работа
-
Характеристика дискретных систем автоматического управления
Дискретные системы автоматического управления как системы, содержащие элементы, которые преобразуют непрерывный сигнал в дискретный. Импульсный элемент (ИЭ), его математическое описание. Цифровая система автоматического управления, методы ее расчета.
-
Расчет и моделирование цифрового фильтра
Изучение сущности цифровой фильтрации - выделения в определенном частотном диапазоне с помощью цифровых методов полезного сигнала на фоне мешающих помех. Особенности КИХ-фильтров. Расчет цифрового фильтра. Моделирование работы цифрового фильтра в MatLab.
-
Разработка цифрового фазового корректора
Представление функциональной и электрической принципиальной схем цифрового фазового корректора. Написание общего алгоритма действия и создание программы фильтра на языке команд микропроцессора. Проведение расчета быстродействия и устойчивости устройства.
-
Разработка устройств цифрового формирования и обработки сигналов системы передачи дискретных сообщений по частотно ограниченным каналам связи
Методы цифровой обработки сигналов в радиотехнике. Информационные характеристики системы передачи дискретных сообщений. Выбор длительности и количества элементарных сигналов для формирования выходного сигнала. Разработка структурной схемы приемника.
-
Реализация и анализ цифрового фильтра с конечной импульсной характеристикой
Министерство образования Российской Федерации УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Оценка работы Курсовая работа Реализация и анализ цифрового фильтра с конечной импульсной характеристикой
-
Проектирование радиоэлектронных средств с помощью ЭВМ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Воронежский государственный технический университет Кафедра радиотехники 354-2006 МЕТОДИЧЕСКИЕ УКАЗАНИЯ
-
Реализация и анализ цифрового фильтра с конечной импульсной характеристикой
Расчет цифрового фильтра нижних частот с конечной импульсной характеристикой. Синтез фильтра методом окна (параболического типа). Свойства фильтра: устойчивость, обеспечение совершенно линейной фазочастотной характеристики. Нахождение спектра сигнала.