Название: Способ определения живучести связи вероятности связности
Вид работы: реферат
Рубрика: Коммуникации и связь
Размер файла: 51.97 Kb
Скачать файл: referat.me-170914.docx
Краткое описание работы: СПОСОБ ОПРЕДЕЛЕНИЯ ЖИВУЧЕСТИ. Определению живучести связи (вероятности связности) между двумя конкретными узлами сети i и j посвящен целый ряд работ [1-5]. Однако расчет точного ее назначения сопряжен с большими вычислительными трудностями. Представляет интерес найти простой способ определения вероятности связности сети, который позволял бы оперативно и вручную проводить на стадии проектирования оценку различных вариантов их построения.
Способ определения живучести связи вероятности связности
СПОСОБ ОПРЕДЕЛЕНИЯ ЖИВУЧЕСТИ.
Определению живучести связи (вероятности связности) между двумя конкретными узлами сети i и j посвящен целый ряд работ [1-5]. Однако расчет точного ее назначения сопряжен с большими вычислительными трудностями. Представляет интерес найти простой способ определения вероятности связности сети, который позволял бы оперативно и вручную проводить на стадии проектирования оценку различных вариантов их построения.
Рассмотрим сеть той же мостиковой структуры, что и в [1] (рис.1). Для простоты будем полагать вероятности исправного функционирования всех ребер сети одинаковыми и равными р
, а неисправного функционирования - равными q
=1-
p
.
Для оценки живучести воспользуемся методом прямого перебора состояний элементов сети связи [5]. На основании биноминального закона вероятность пребывания сети связи в состоянии, когда i любых ребер сети отказали,![]() , где
, где ![]() - биноминальный коэффициент; N – число ребер сети.
- биноминальный коэффициент; N – число ребер сети.
Например, для сети, изображенной на рис. 1, живучесть связи р13 зависит от следующей
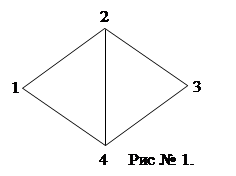
совокупности независимых событий: исправного состояния сети в целом – вероятность этого события равна р
3
; повреждения любого одного ребра сети – вероятность ![]() одновременного повреждения любых двух ребер сети, за исключением двух случаев, когда оба ребра подходят к узлу 1 или к узлу 3 – вероятность
одновременного повреждения любых двух ребер сети, за исключением двух случаев, когда оба ребра подходят к узлу 1 или к узлу 3 – вероятность![]() одновременного повреждения трех ребер сети, подходящих к узлу 2 или 4 – вероятность 2р2
q3
.
одновременного повреждения трех ребер сети, подходящих к узлу 2 или 4 – вероятность 2р2
q3
.
Суммируя все вероятности независимых событий, получаем искомое выражение :
![]()
что полностью совпадает полученными результатами в [1].
Аналагично для всех остальных пар узлов сети рис. № 1.
![]()
![]()
Из анализа видно, что
![]()
Связанной сетью являются сеть, в которой любой из узлов соединен с остальными узлами сети. Вероятность связанности сети рис. № 1
![]()
так как эта сеть допускает все одиночные повреждения ребер и восемь двойных повреждений ребер. Вероятность связности сети меньше или равна живучести связи между любой парой узлов сети, в данном случае рс <р13 .
С точки зрения характеристики сети интерес представляют вероятность рс , минимальная рмин и максимальная рмакс живучести связи между любой парой узлов сети и соотношения между ними. Для сети рис №1: рс < рмин = р13 < р12 = р14 = р23 = р34 < р24 =рмакс .
Аналогично можно найти выражения для вероятности связности полносвязных сетей. Для сети с тремя вершинами (n=3)
![]() (1)
(1)
для n=4;
![]() (2)
(2)
для n=5;
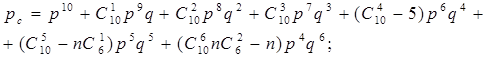 (3)
(3)
для n=6;
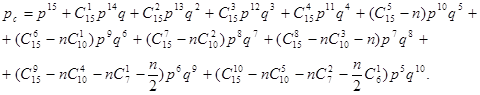 (4)
(4)
Для рс при n=7….10 расчетные формулы не приводятся из-за громоздкости.
Вероятность связности для кольцевых сетей связи, т.е. сетей, у которых степень для каждой вершины равна 2 (степенью вершины d называются число граней графа сети, инцидентных данной вершине [6]),
![]()
На рис 2 определена зависимость рс от р для кольцевых сетей при различных n. Из ее анализа видно, что вероятность связности кольцевых сетей падает с увеличением числа узлов сети при одних и тех же значениях р.
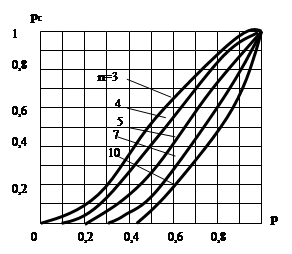 |
Рис № 2.
 |
На практике довольно редко встречаются полносвязные сети. Обычно бывают сети с небольшимистепенями вершин. Имеется большое семейство графов (так называемых равнопрочных) , в которых степень вершины d, число вершин n и общее число граней m связаны следующим соотношением: d=2m/n (при n>2).
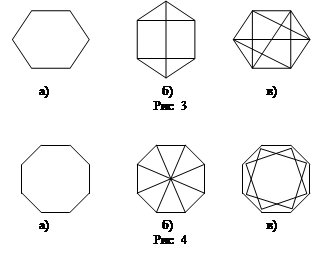
Например для шестиугольника (n=6) без резервирования связей можно построить четыре различных графа с d=2, 3, 4, 5. Вероятности связности этих графов определяется следующими выражениями:
При d=2 (рис. 3,а)
![]() (5)
(5)
при d=3 (рис. 3,б)
![]() (6)
(6)
при d=4 (рис. 3,в)
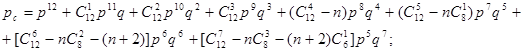 (7)
(7)
При n=8 можно построить шесть различных графов с d=2…..7; вероятность связности этих графов определится следующими выражениями:
d=2 (рис. 4,а)
![]() (8)
(8)
d=3 (рис. 4,б)
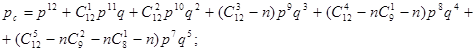 (9)
(9)
d=4 (рис. 4,в)
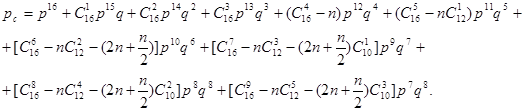 (10)
(10)
 |
 |
Расчетные формулы для рс при d=5 и 6 из-за громоздкости не приводятся.
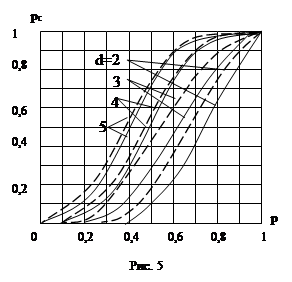
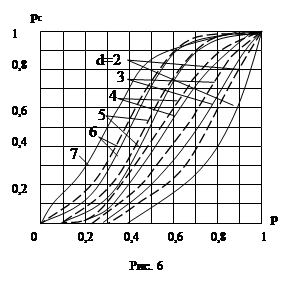
На рис 5 и 6 представлены зависимости вероятности связности сети с n=6, 8 соответственно при различных d (сплошные линии), построенные по формулам (5) – (10). Из рисунков видно, что увеличение вероятности связности сети с увеличением d при неизменном p объясняется тем , что с увеличением d возрастает разветвленность сети связи.
К сожалению, ловольно трудно получить аналитическое выражение для вероятности связности сети рассматренного семейство графов при различных d и n, за исключением полносвязных сетей с d = n – 1 [см.выражение (1) – (4)]. По этому целесобразно определять верхнюю груницу вероятности связности графов. Если граф связный, то в нем не может быть изолированных вершин. В этом случае каждой вершине должна быть инцидента по крайней мере одна ветвь.
Пусть Ai – событие, когда не существует неповрежденных ветвей, инцидентных вершине i, p(Ai ) – вероятность этого события; 1 – p(Ai ) – вероятность дополнительного события, когда существует по крайней мере одна целая ветвь, инцидентная вершине i, Поэтому вероятность того, что у всех вершин есть по крайне мере одна целая ветвь, т.е. есть связана, ограничена неравенством:
![]() (11)
(11)
На рис. 5,6 представлены зависимости (11) для n=6, и d=2…..7 (штриховые линии). Сравнение кривых показывает, что верхнюю границу вероятности связности сети, особенно при больших d.
Таким образом, полученная простая верхняя оценка вероятности связности равнопрочных сетей связи дает шорошее приближение к точному значению вероятности связности сети при больших значениях d.
Похожие работы
-
Методы поиска отказов
Теоретические основы поиска, отказа - диагностирования, целью которого является определение места и при необходимости причины и вида отказа объекта. Особенности измерения диагностических признаков (проверки): время, масса оборудования, его стоимость.
-
Выбор метода конструирования и документирования электронных средств
Проектирование современных электронных средств и характеристика существующих методов их конструирования. Государственные стандарты оформления конструкторской документации, их учет и хранение в бюро технической документации. Виды носителей информации.
-
Основы построения телекоммуникационных систем
Содержание Введение _______________________________ 2 Техническое задание _____________________ 3 Расчет количества линий коммутируемого доступа
-
Методы размещения и трассировки печатных плат на примере модуля памяти
Содержание ВВЕДЕНИЕ 2 1. ВЫБОР СЕРИИ И ТИПОВ МИКРОСХЕМ И РАСПРЕДЕЛЕНИЕ ЭЛЕМЕНТОВ ФУНКЦИОНАЛЬНОЙ СХЕМЫ ПО КОРПУСАМ. 3 1.1. Выбор физических элементов для реализации схемы и обзор параметров выбранной серии. 3
-
Разработка системы кодированиядекодирования циклического кода
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра КТРС РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ ПО ДИСЦИПЛИНЕ
-
Определение межповерочных и межкалибровочных интервалов СИ
Критерии для определения межповерочного интервала, методика определения МПИ. Показатели метрологической надежности. Методы количественного обоснования МПИ. Корректировка МПИ в процессе эксплуатации СИ. Оптимизация МПИ по экономическому критерию.
-
Разработка печатного модуля РЭС с использованием учебных алгоритмов САПР
Решение задачи компоновки для функциональной схемы с использованием последовательного алгоритма, пошаговое описание алгоритма. Размещение элементов в принципиальной электрической схеме. Трассировка цепей питания и земли с помощью волновых алгоритмов.
-
Оценка эффективности устройств СДЦ радиолокационных станций с ОВНЦ по целевым показателям
Основные задачи, стоящие перед радиолокационными станциями с селекцией движущихся целей. Методика оценки эффективности РЛС с СДЦ на основе сравнительного анализа вероятности правильного обнаружения с учетом влияния кривизны Земли и затухания радиоволн.
-
Расчет структурной надежности системы
Структурная схема надежности технической системы. Построение графика изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 - 0.2. Анализ зависимостей вероятностей безотказной работы.
-
Основы комплексной автоматизации и проектирования ЭВМ
Лабораторные работы № 1- 4 По дисциплине: «Автоматизация проектирования ЭВМ» Содержание Лабораторная работа № 1 Электрическая функциональная схем