Название: Статистические методы обработки выборочных данных наблюдений или экспериментов
Вид работы: курсовая работа
Рубрика: Экономика
Размер файла: 468.54 Kb
Скачать файл: referat.me-376436.docx
Краткое описание работы: Первичный анализ экспериментальных данных. Построение эмпирической плотности распределения случайной анализируемой величины и расчет ее характеристик. Определение вида закона распределения величины и расчёт его параметров при помощи метода моментов.
Статистические методы обработки выборочных данных наблюдений или экспериментов
ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Институт транспортной техники и организации производства
(ИТТОП)
Кафедра: «Локомотивы и локомотивное хозяйство»
Курсовой проект
на тему:
«Статистические методы обработки выборочных данных наблюдений или экспериментов»
Выполнил: студент Краснов М.А.
группы ТЛТ-451
Принял: Пузанков А.Д.
Москва 2009
СОДЕРЖАНИЕ
1. ПЕРВИЧНЫЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
2. ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ АНАЛИЗИРУЕМОЙ ВЕЛИЧИНЫ И РАСЧЕТ ЕЕ ХАРАКТЕРИСТИК
3. ОПРЕДЕЛЕНИЕ ВИДА ЗАКОНА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И РАСЧЕТ ЕГО ПАРАМЕТРОВ ПРИ ПОМОЩИ МЕТОДА МОМЕНТОВ
4. ОПРЕДЕЛЕНИЕ ВИДА ТЕОРЕТИЧЕСКОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ГРАФИЧЕСКИМ МЕТОДОМ
1. Первичный анализ экспериментальных данных
Запишем полученные значения в вариационный ряд в возрастающем порядке:
Таблица 1.
| 16,4 |
21,6 |
35,46 |
38,76 |
39,84 |
40,65 |
44,25 |
46,73 |
47,62 |
50,25 |
| 50,25 |
51,02 |
51,8 |
55,22 |
55,25 |
55,55 |
61,73 |
63,3 |
64,93 |
67,56 |
| 68,5 |
68,5 |
71,94 |
73 |
73,53 |
73,53 |
74,07 |
77,52 |
78,12 |
78,74 |
| 78,74 |
80,64 |
85,47 |
86,2 |
87,72 |
90,1 |
92,6 |
94,34 |
95,24 |
96,15 |
| 99,01 |
99,01 |
106,4 |
108,6 |
116,28 |
133,3 |
135,13 |
137 |
144,93 |
149,25 |
| 153,84 |
161,3 |
166,7 |
172,4 |
172,4 |
175,44 |
178,6 |
178,6 |
185,18 |
192,3 |
| 208,33 |
212,76 |
227,27 |
232,56 |
238,1 |
243,9 |
256,41 |
277,8 |
277,8 |
285,7 |
| 285,71 |
285,71 |
322,6 |
322,6 |
344,83 |
370,4 |
370,4 |
370,4 |
384,6 |
420,6 |
| 526,3 |
555,55 |
588,23 |
943,4 |
xmax = 943,4; xmin = 16,4
Результат последних двух измерений вызывает сомнения. Поэтому выполняем проверку:
Величину выборочного среднего ![]() находим из соотношения:
находим из соотношения:
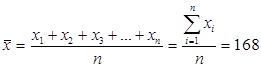 (1)
(1)
Корень квадратный из дисперсии, взятый с положительным знаком, называется среднеквадратическим отклонением и рассчитывается по формуле:
![]()
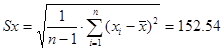 (2)
(2)
Упрощённая проверка сомнительного результата на брак выполняется из условия:
![]()
![]()
Таким образом, по упрощенной проверке результат сомнительного измерения браком являются последнее одно значение, отбрасываем их и пересчитываем ![]() и
и ![]() :
: ![]()
Проверяем по упрощённой проверки:
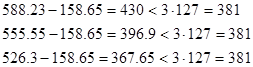
Таким образом, по упрощенной проверке результат сомнительного измерения браком являются последние два значения, отбрасываем их и пересчитываем ![]() и
и ![]() :
: ![]()
![]()
Таким образом, по упрощенной проверке результат сомнительного измерения браком являются последнее одно значение, отбрасываем их и пересчитываем ![]() и
и ![]() :
: ![]()
![]()
Таким образом, по упрощенной проверке результат сомнительного измерения не является браком.
Так же выполним подобную проверку с помощью критерия Ирвина:
![]()
![]()
Таким образом, по расчётам обеих проверок результат последнего сомнительного измерения не является браком.
Из этого следует, что нужно произвести повторный расчёт, но уже без данного измерения:
![]()
2. Построение эмпирической плотности распределения случайной анализируемой величины и расчёт её характеристик
Определяем размах имеющихся данных, т.е. разности между наибольшим и наименьшим выборочным значениями (R = Xmax – Xmin):
![]()
Выбор числа интервалов группировки k при числе наблюдений n<100 – ориентировочное значение интервалов можно рассчитать с использованием формулы Хайнхольда и Гаеде:
![]()
Тогда ширина интервала:
![]()
Результат подсчёта частот и характеристик эмпирического распределения
Таблица 2.
| Границы интервала группировки |
Ср.знач. интерв. |
Распределение данных |
fi |
U |
U*f |
U^2*f |
| 16,4…61,31 |
38,86 |
//////////////// |
16 |
-1 |
-16 |
16 |
| 61,31…106,22 |
83,77 |
////////////////////////// |
26 |
0 |
0 |
0 |
| 106,22…151,13 |
128,68 |
//////// |
8 |
1 |
8 |
8 |
| 151,13…196,04 |
173,59 |
////////// |
10 |
2 |
20 |
40 |
| 196,04…240,96 |
218,50 |
///// |
5 |
3 |
15 |
45 |
| 240,96…285,87 |
263,41 |
///// |
5 |
4 |
20 |
80 |
| 285,87…330,78 |
308,32 |
//// |
4 |
5 |
20 |
100 |
| 330,78…375,69 |
353,23 |
//// |
4 |
6 |
24 |
144 |
| 375,69…420,60 |
398,14 |
// |
2 |
7 |
14 |
98 |
| ИТОГО |
80 |
105 |
531 |
|||
Принимаем «ложный нуль» x0 =83,77 и обозначаем нулем тот интервал, которому соответствует максимальная частота (f=26). Далее, для интервалов, следующих к наименьшему наблюдаемому значению вписываем -1, -2 … и 1, 2, … для интервалов, следующих к наибольшему значению наблюдаемой величины.
Выборочное среднее х и среднеквадратическое отклонение Sx рассчитываем, используя следующие выражения:
![]() (3)
(3)
![]()
Для построения гистограммы, приведённой на рис.1, по оси абсцисс в выбранном масштабе отмечаем границы интервалов. Левая ось размечается масштабом частот, а на правую, в случае необходимости, можно нанести шкалу относительных частот. На чистом поле гистограммы указываются значения: числа данных; среднего арифметического; среднеквадратического отклонения.
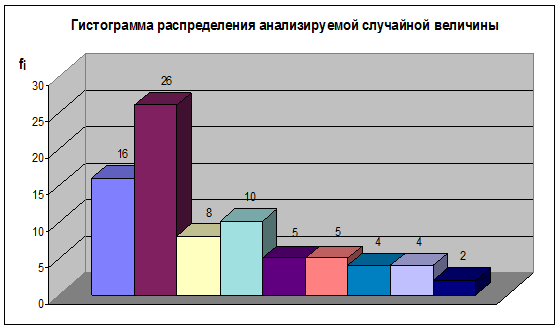
Рис.1
Помимо гистограммы эмпирические данные измерений случайной величины могут быть представлены в виде кумулятивной кривой функции распределения вероятностей. Для этого данные, представленные в табл.1., должны быть дополнены частостями (см. табл.2.).
Частость находим из соотношения:
![]()
Таблица частот f и частостей ω.
Таблица 3.
| Границы интервала группировки |
Частота,fi |
Частость, ω i |
Накопленная частость, ω н |
| 16,4…61,31 |
16 |
0,20 |
0,20 |
| 61,31…106,22 |
26 |
0,33 |
0,53 |
| 106,22…151,13 |
8 |
0,10 |
0,63 |
| 151,13…196,04 |
10 |
0,13 |
0,75 |
| 196,04…240,96 |
5 |
0,06 |
0,81 |
| 240,96…285,87 |
5 |
0,06 |
0,88 |
| 285,87…330,78 |
4 |
0,05 |
0,93 |
| 330,78…375,69 |
4 |
0,05 |
0,98 |
| 375,69…420,60 |
2 |
0,03 |
1,00 |
| ИТОГО |
80 |
1 |
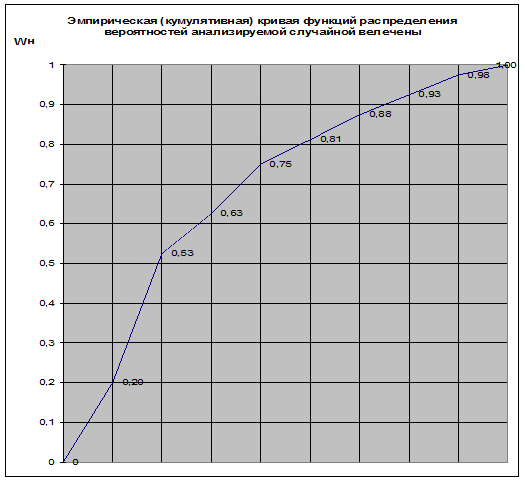
Рис. 2
3. Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов
Экспоненциальный (нормальный) закон распределения
Параметр закона распределения: ![]()
Таблица 4
| № |
xi 103 км |
fi шт |
λ*xi |
e-λ*xi |
φ(xi) 10-6 |
fi’ шт |
|
| 1 |
38,86 |
16 |
0,270 |
0,763 |
0,531 |
19,08 |
0,50 |
| 2 |
83,77 |
26 |
0,583 |
0,558 |
0,388 |
13,96 |
10,39 |
| 3 |
128,68 |
8 |
0,895 |
0,408 |
0,284 |
10,21 |
0,48 |
| 4 |
173,59 |
10 |
1,208 |
0,299 |
0,208 |
7,47 |
0,86 |
| 5 |
218,50 |
5 |
1,520 |
0,219 |
0,152 |
5,47 |
0,04 |
| 6 |
263,41 |
5 |
1,833 |
0,160 |
0,111 |
4,00 |
0,25 |
| 7 |
308,32 |
4 |
2,145 |
0,117 |
0,081 |
2,93 |
0,39 |
| 8 |
353,23 |
4 |
2,458 |
0,086 |
0,060 |
2,14 |
1,62 |
| 9 |
398,14 |
2 |
2,770 |
0,063 |
0,044 |
1,57 |
0,12 |
| ИТОГО: |
80 |
14,64 |
|||||
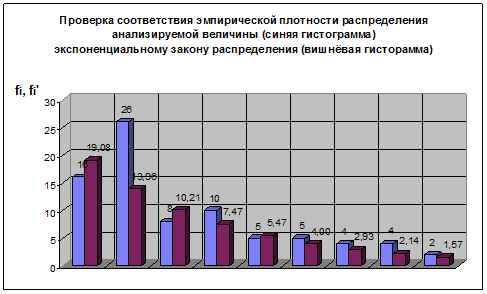
Рис. 4
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 7 и ![]() = 14,067.
= 14,067.
Так как χ2 > χ0,05 2 , то гипотеза о принадлежности эмпирической выборки значений, экспоненциальному закону распределения отвергается
Распределение Вейбулла - Гнеденко
Величина выборочного коэффициента вариации:
![]()
По данным приложения таблица П1,2:
![]()
![]()
Таблица 5
| № |
Xi 103 км |
fi шт |
xi/a |
a* φ(xi) |
φ(xi) 10-6 |
fi’ шт |
|
| 1 |
38,86 |
16 |
0,246 |
0,6944 |
4,4017 |
15,81 |
0,00 |
| 2 |
83,77 |
26 |
0,531 |
0,7197 |
4,5618 |
16,39 |
5,63 |
| 3 |
128,68 |
8 |
0,816 |
0,6085 |
3,8567 |
13,86 |
2,48 |
| 4 |
173,59 |
10 |
1,100 |
0,4637 |
2,9393 |
10,56 |
0,03 |
| 5 |
218,50 |
5 |
1,385 |
0,3293 |
2,0870 |
7,50 |
0,83 |
| 6 |
263,41 |
5 |
1,670 |
0,2213 |
1,4029 |
5,04 |
0,00 |
| 7 |
308,32 |
4 |
1,954 |
0,1422 |
0,9014 |
3,24 |
0,18 |
| 8 |
353,23 |
4 |
2,239 |
0,0879 |
0,5570 |
2,00 |
2,00 |
| 9 |
398,14 |
2 |
2,524 |
0,0525 |
0,3325 |
1,19 |
0,54 |
| ИТОГО: |
80 |
75,60 |
11,69 |
||||
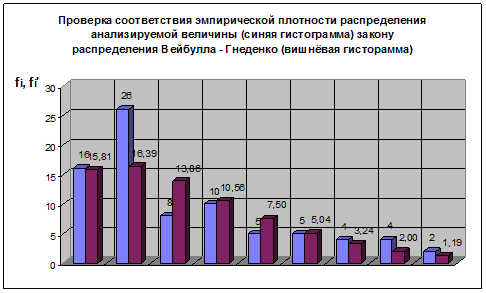
Рис. 5
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и ![]() = 12,592.
= 12,592.
Так как χ2 > χ0,05 2 , то эмпирическая выборка значений пренадлежит закону распределения Вейбулла - Гнеденко
Нормальный (Гауссовский) закон распределения
Таблица 6
| № |
Xi 103 км |
fi |
ti |
φ(ti) 10-2 |
φ(xi) |
fi’ щт |
|
| 1 |
38,86 |
16 |
-1,025 |
0,231 |
0,101 |
8,09 |
7,72 |
| 2 |
83,77 |
26 |
-0,586 |
0,328 |
0,144 |
11,52 |
18,18 |
| 3 |
128,68 |
8 |
-0,147 |
0,386 |
0,169 |
13,53 |
2,26 |
| 4 |
173,59 |
10 |
0,292 |
0,374 |
0,164 |
13,11 |
0,74 |
| 5 |
218,50 |
5 |
0,731 |
0,298 |
0,131 |
10,48 |
2,86 |
| 6 |
263,41 |
5 |
1,169 |
0,197 |
0,086 |
6,91 |
0,53 |
| 7 |
308,32 |
4 |
1,608 |
0,107 |
0,047 |
3,75 |
0,02 |
| 8 |
353,23 |
4 |
2,047 |
0,048 |
0,021 |
1,68 |
3,18 |
| 9 |
398,14 |
2 |
2,486 |
0,018 |
0,008 |
0,62 |
3,04 |
| ИТОГО: |
80 |
69,71 |
38,54 |
||||
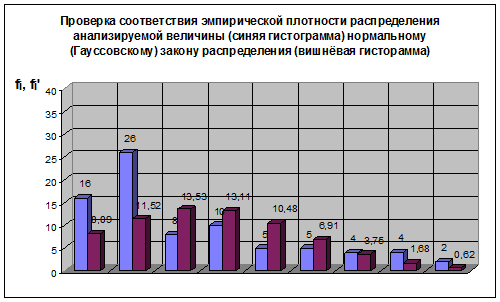
Рис. 6
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и ![]() = 12.592.
= 12.592.
Так как χ2 > χ0,05 2 , то гипотеза о принадлежности эмпирической выборки значений, нормальному (Гауссовскому) закону распределения отвергается
Логарифмически - нормальный закон распределения
Значения средне-выборочное и средне-квадратичное:
![]()
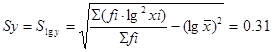
Таблица 7
| № |
Xi 103 км |
fi |
ti |
φ(ti) |
φ(xi) |
fi’ щт |
|
| 1 |
38,86 |
16 |
-1,481 |
0,133 |
4,808 |
17,28 |
0,094 |
| 2 |
83,77 |
26 |
-0,404 |
0,367 |
6,155 |
22,12 |
0,682 |
| 3 |
128,68 |
8 |
0,198 |
0,391 |
4,263 |
15,32 |
3,494 |
| 4 |
173,59 |
10 |
0,618 |
0,329 |
2,663 |
9,57 |
0,019 |
| 5 |
218,50 |
5 |
0,941 |
0,256 |
1,645 |
5,91 |
0,140 |
| 6 |
263,41 |
5 |
1,203 |
0,193 |
1,030 |
3,70 |
0,455 |
| 7 |
308,32 |
4 |
1,423 |
0,144 |
0,659 |
2,37 |
1,126 |
| 8 |
353,23 |
4 |
1,614 |
0,108 |
0,430 |
1,55 |
3,892 |
| 9 |
398,14 |
2 |
1,782 |
0,081 |
0,287 |
1,03 |
0,908 |
| ИТОГО: |
80 |
10,81 |
|||||
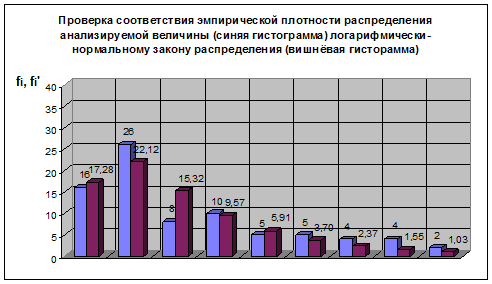
Рис. 7
Нормальный закон распределения двухпараметрический, число степеней свободы υ = 6 и ![]() = 12.592.
= 12.592.
Так как χ2 < χ0,05 2 , то эмпирическая выборка значений принадлежит логарифмически-нормальному закону распределения
4. Определение вида теоретического закона распределения случайной величины графическими методами
Расчёт координат эмпирических точек заданной выборки
Таблица 8.
| № п/п |
Среднее значение интервала xi , 103 км |
fi , шт |
Σ fi |
F(x)= Σ fi /n+1 |
| 1 |
38,86 |
16 |
16 |
0,198 |
| 2 |
83,77 |
26 |
42 |
0,519 |
| 3 |
128,68 |
8 |
50 |
0,617 |
| 4 |
173,59 |
10 |
60 |
0,741 |
| 5 |
218,50 |
5 |
65 |
0,802 |
| 6 |
263,41 |
5 |
70 |
0,864 |
| 7 |
308,32 |
4 |
74 |
0,914 |
| 8 |
353,23 |
4 |
78 |
0,963 |
| 9 |
398,14 |
2 |
80 |
0,988 |
Используя полученные в табл.4. данные, строим вероятностную сетку и выполняем проверку согласованности.
Выбор масштаба построения вероятностной сетки:
· ширина графика (ось абсцисс) А = 140 мм ;
· высота графика (ось ординат) Н = 180 мм .
Нормальный закон распределения
Масштаб значений оси абсцисс устанавливается на основе выражения:
![]()
Таблица 9
| P = F(x) |
0,5 |
0,6 |
0,7 |
0,8 |
0,8413 |
0,85 |
0,903 |
| y = Q-1 (P) |
0 |
0,25 |
0,52 |
0,85 |
1 |
1,05 |
1,3 |
| Ky (P), мм |
0 |
7,5 |
15,6 |
25,5 |
30 |
31,5 |
39 |
| P = F(x) |
0,96 |
0,971 |
0,98 |
0,991 |
0,9953 |
0,997 |
0,9987 |
| y = Q-1 (P) |
1,75 |
1,9 |
2,05 |
2,35 |
2,6 |
2,75 |
3 |
| Ky(P), мм |
52,5 |
57 |
61,5 |
70,5 |
78 |
82,5 |
90 |
Лгарифмически - нормальный закон распределения
Масштаб значений оси абсцисс устанавливается на основе выражения:
![]()
Таблица 10
| № |
Границы интервала |
xi 103 км |
|
|
| 1 |
418,78…475,69 |
38,86 |
456,01 |
0,198 |
| 2 |
475,69…499,40 |
83,77 |
489,15 |
0,519 |
| 3 |
499,40…514,62 |
128,68 |
507,68 |
0,617 |
| 4 |
514,62…525,85 |
173,59 |
520,60 |
0,741 |
| 5 |
525,85…534,75 |
218,50 |
530,52 |
0,802 |
| 6 |
534,75…542,12 |
263,41 |
538,59 |
0,864 |
| 7 |
542,12…548,42 |
308,32 |
545,38 |
0,914 |
| 8 |
548,42…553,91 |
353,23 |
551,25 |
0,963 |
| 9 |
553,91…558,78 |
398,14 |
556,42 |
0,988 |
![]()
![]()
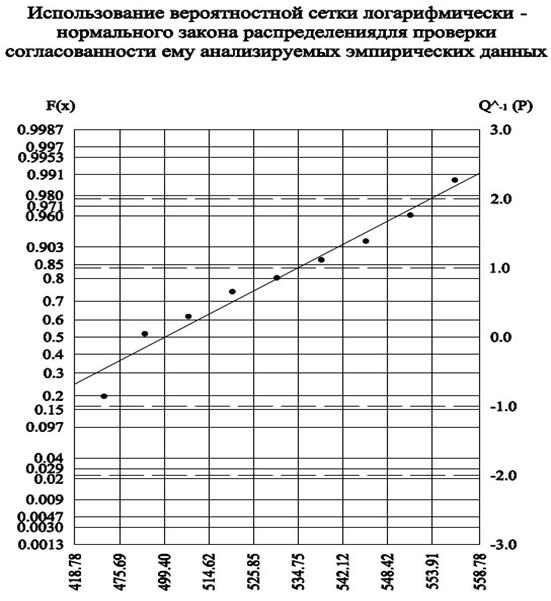
Экспоненциальный (нормальный) закон распределения
Таблица 11
| P = F(x) |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
| Ky (P), мм |
0,0 |
3,2 |
6,7 |
10,7 |
15,3 |
20,8 |
27,5 |
36,1 |
| P = F(x) |
0,8 |
0,9 |
0,95 |
0,97 |
0,98 |
0,99 |
0,995 |
0,9975 |
| Ky(P), мм |
48,3 |
69,1 |
89,9 |
105,2 |
117,4 |
138,2 |
158,9 |
179,7 |
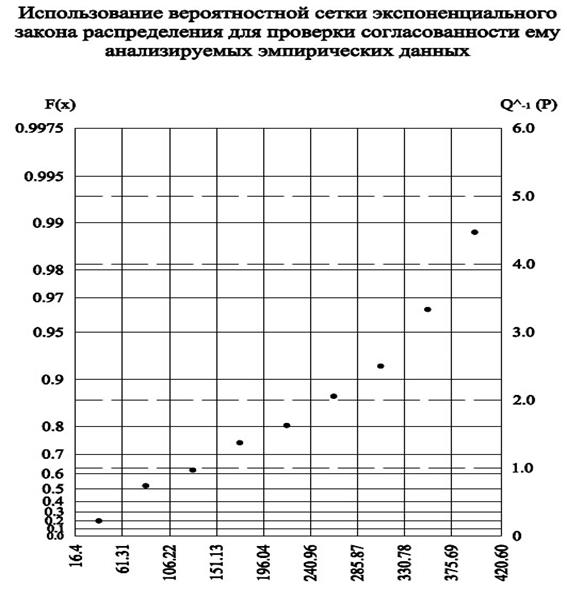
Распределение Вейбулла – Гнеденко
Таблица 12
| P = F(x) |
0,03 |
0,04 |
0,06 |
0,1 |
0,2 |
0,3 |
0,4 |
| y = Q-1 (P) |
-3,5 |
-3,2 |
-2,8 |
-2,25 |
-1,5 |
-1,03 |
-0,7 |
| Ky (P), мм |
-118,8 |
-108,6 |
-95,0 |
-76,4 |
-50,9 |
-35,0 |
-23,8 |
| P = F(x) |
0,5 |
0,632 |
0,78 |
0,9 |
0,97 |
0,955 |
0,999 |
| y = Q-1 (P) |
-0,36 |
0,00 |
0,41 |
0,83 |
1,25 |
1,66 |
1,93 |
| Ky(P), мм |
-12,2 |
0,00 |
13,9 |
28,2 |
42,4 |
56,3 |
65,5 |
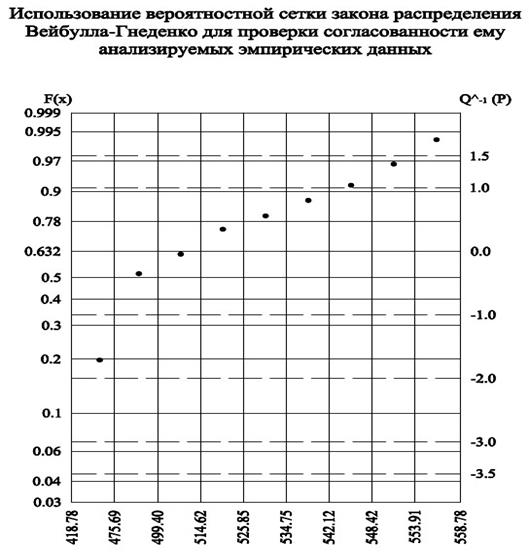
Похожие работы
-
Комплексная статистическая обработка экспериментальных данных
Министерство образования и науки Украины Пояснительная записка к курсовой работе по дисциплине Статистика Комплексная статистическая обработка экспериментальных данных
-
Моделирование рисков инвестиционных проектов
Имитационное моделирование (simulation) является одним из мощнейших методов анализа экономических систем. В общем случае, под имитацией понимают процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира.
-
Организация и планирование ОКР. Расчет затрат и цены. Расчет заработной платы
Экономика Экономика тема : Организация и планирование ОКР. Расчет затрат на тему и ее цены. Расчет заработной платы. 10.1. Организация и планирование ОКР.
-
Использование статистических функций в математическом пакете MathCAD
Основные принципы работы в MathCAD. Типовые статистические функции. Функции вычисления плотности распределения вероятности. Функции и квантили распределения. Функции создания векторов с различными законами распределения. Функции для линейной регрессии.
-
Основные понятия статистики
Законы распределения случайных величин. Закон распределения Пуассона. Свойства плотности вероятности. Критериальные случайные величины. Свойство коэффициента корреляции. Закон больших чисел и его следствия. Предельные теоремы теории вероятностей.
-
Метод наименьших квадратов для однофакторной линейной регрессии
Сущность и применение метода наименьших квадратов для однофакторной линейной регрессии. Нахождение коэффициента эластичности для указанной модели в заданной точке X и его экономический анализ. Прогноз убыточности на основании линейной регрессии.
-
Анализ данных в линейной регрессионной модели
Построение диаграммы рассеивания (корреляционного поля). Группировка данных и построение корреляционной таблицы. Оценка числовых характеристик для негруппированных и группированных данных. Выборочное значение статистики. Параметры линейной регрессии.
-
Расчет статистических показателей
Формирование информационной базы – начальной стадии экономико-статистического исследования. Расчеты средней и предельной ошибок выборки. Оценка распространения выборочных данных на генеральную совокупность. Построение вариационного возрастающего ряда.
-
Описательная статистика
Группировка статистических показателей, описывающих выборку. Этапы построения вариационного ряда, группировки данных. Определение частости и эмпирической плотности вероятностей. Построение полигона, гистограммы и эмпирической функции распределения.
-
Статистические гипотезы
Статистические гипотезы и методы их проверки. Закон распределения случайной величины. Математические ожидания экспоненциально распределенных выборок. Области отклонения гипотезы. Плотность нормального распределения. Плотность распределения Стьюдента.