Название: Статистические методы в экономике

Вид работы: контрольная работа

Рубрика: Экономика

Размер файла: 81.97 Kb

Скачать файл: referat.me-381992.docx

Краткое описание работы: Структурно-аналитическая группировка по двум признакам-факторам, расчет среднего значения группировочного признака. Сущность правила сложения дисперсий и коэффициента регрессии. Характеристика и расчет систематической вариации результативного порядка.

Статистические методы в экономике

Задача 1

Провести структурно-аналитическую группировку 20 регионов страны (см. табл.3) по двум признакам-факторам, положив в основание группировки нижеуказанный для конкретного варианта признак. Рассчитайте среднее значение группировочного признака по каждой группе. Результаты отобразить в статистической таблице, оформленной в соответствии с установленными правилами.

Постройте графически полученный ряд распределения признака в виде гистограммы.

По результатам группировки определите:

- показатели центра распределения: средние арифметическое значение группировочного признака моду и медиану;

- показатели вариации признака:

- абсолютные показатели: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия.

- относительные показатели: коэффициенты осцилляции, вариации и линейной вариации;

- сделайте вывод о форме распределения на основании расчета коэффициентов асимметрии и эксцесса.

По результатам расчетов сделать вывод.

Таблица 1

Вариант	Регион
3	с 10 по 29

Выбор группировочного признака осуществляется по следующей схеме, представленной в таблице 2.

Таблица 2

Вариант	Группировочный признак
с 1 по 4	«ВРП»

Исходные данные

Таблица 3

Регион	ВВП, млн.руб.	Потребительские расходы, млн.руб.	Государственные расходы, млн.руб.	Валовые инвестиции, млн.руб.	Экспорт, млн.руб.	Средняя зп, руб.
10	36,6	18,3	3,7	6,6	8,4	2150
11	39,2	19,6	3,9	7,1	9,0	2300
12	41,8	20,9	4,2	7,5	9,6	2450
13	44,4	22,2	4,4	8,0	10,2	2600
14	66,0	33,0	6,6	11,9	15,2	2750
15	68,6	34,3	6,9	12,3	15,8	2900
16	71,2	35,6	7,1	12,8	16,4	3050
17	73,8	36,9	7,4	13,3	17,0	1900
18	35,0	17,5	3,5	6,3	8,1	2050
19	37,6	18,8	3,8	6,8	8,6	2200
20	40,2	20,1	4,0	7,2	9,2	2350
21	42,8	21,4	4,3	7,7	9,8	2500
22	55,0	27,5	5,5	9,9	12,7	2650
23	57,6	28,8	5,8	10,4	13,2	2360
24	60,2	30,1	6,0	10,8	13,8	2510
25	60,0	30,0	6,0	10,8	13,8	2660
26	62,6	31,3	6,3	11,3	14,4	2810
27	65,2	32,6	6,5	11,7	15,0	2960
28	67,8	33,9	6,8	12,2	15,6	2000
29	70,4	35,2	7,0	12,7	16,2	2150

РЕШЕНИЕ

Группировка - это разбиение совокупности на группы, однородные по какому-либо признаку. Метод группировок основывается на 2-х категориях: группировочный признак и интервал. Группировочный признак - это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Интервал - очерчивает количественные границы групп.

Величину интервала в данной задаче можно определить следующим образом:

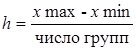(1)

х max, xmin - максимальное и минимальное значение варьирующего признака. Для нахождения числа групп служит формула Стерджесса:

(2)

1. Сначала определим количество групп (2):

где N - количество элементов совокупности. N =20

=5,32, значит групп 5

1. Определим длину интервала по формуле (1):

=7,76 млн.руб.

Величина интервала 7,76 млн.руб.

35,0 – 42,76; 42,76-50,52; 50,52 – 58,28; 58,28 – 66,04; 66,04 – 73,8

Таблица 4

№ группы	Группировка по ВВП	№ региона	ВВП, млн.руб.
I	35,0 – 42,76	18	35,0
		10	36,6
		19	37,6
		11	39,2
		20	40,2
		12	41,8
II	42,76-50,52	21	42,8
		13	44,4
III	50,52 – 58,28	22	55,0
		23	57,6
IV	58,28 – 66,04	14	66,0
		27	65,2
		25	60,0
		24	60,2
		26	62,6
		28	67,8
		15	68,6
V	66,04 – 73,8	16	71,2
		17	73,8
		29	70,4

При построении вариационного ряда все расчеты отражаем в таблице.

Таблица 5

Инвестиции в основные фонды	Числорегионов,	Серединаинтервала,
35,0 – 42,76	6	38,88	233,28	251241,53	5024830,6
42,76-50,52	2	46,64	93,28	243522,51	4870450,2
50,52 – 58,28	2	54,4	108,8	235923,91	4718478,2
58,28 – 66,04	7	62,16	435,12	228445,76	4568915,2
66,04 – 73,8	3	69,92	209,76	221088,04	4421760,8
Итого	20	272	1080,24	1180222	23604435

Средняя величина - выражает величину признака, отнесенную к единице совокупности.

- средняя арифметическая взвешенная

- средняя арифметическая простая

где X_i - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

n- число наблюдение;

f_i - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

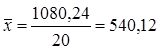
Показатели вариации:

- размах вариации:

,

где х_max - максимальное значение признака,

х _min – минимальное значение признака;

R=73,8-35,0=38,8

- среднее линейное отклонение:

- ,

где – индивидуальные значения признака,

– средняя величина,

f– частота;

d=272-540,12=268,12

- дисперсия:

;

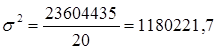
- среднее квадратическое отклонение:

;

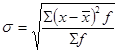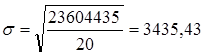
- коэффициент вариации:

.

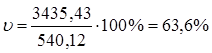
Коэффициент вариации показывает степень однородности совокупности. Так как V > 33% - совокупность неоднородна.

- коэффициент осцилляции:

V=38,8/540,12*100%=7,18

- линейный коэффициент вариации:

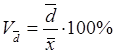
V=268,12/540,12*100%=49,64

2. Производим группировку по второму признаку: Валовые инвестиции, млн.руб.

Величина интервала:

h= у max - у min /число групп

у max, у min - максимальное и минимальное значение варьирующего признака

Для нахождения числа групп служит формула Стерджесса

1. Сначала определим количество групп:

где N - количество элементов совокупности. N =20

=5,32,

значит групп 5

1. Определим длину интервала по формуле (1):

h=13,3-6,3/5=1,4 млн.руб.

Величина интервала 1,4 млн.руб.

6,3 – 7,7; 7,7-9,1; 9,1 – 10,5; 10,5 – 11,9; 11,9 – 13,3

Таблица 6

№ группы	Группировка по Валовым инвестициям, млн.руб	№ региона	Валовые инвестиции, млн.руб
I	6,3 – 7,7	12	7,5
		18	6,3
		10	6,6
		19	6,8
		11	7,1
		20	7,2
II	7,7-9,1	21	7,7
		13	8,0
III	9,1 – 10,5	22	9,9
		23	10,4
IV	10,5 – 11,9	14	11,9
		27	11,7
		25	10,8
		24	10,8
		26	11,3
V	11,9 – 13,3	28	12,2
		16	12,8
		17	13,3
		29	12,7
		15	12,3

При построении вариационного ряда все расчеты отражаем в таблице.

Таблица 7

Валовые инвестиции, млн.руб	Числорегионов,	Серединаинтервала,
6,3 – 7,7	6	7,0	43	8,5264	51
7,7-9,1	2	8,4	16,8	2,31	4,62
9,1 – 10,5	2	8,8	19,6	1,2544	2,5
10,5 – 11,9	5	11,2	56	1,6384	8,2
11,9 – 13,3	5	12,6	63	7,1824	35,9
Итого	20	60,6	198,4	20,9116	102,22

Средняя величина - выражает величину признака, отнесенную к единице совокупности.

- средняя арифметическая взвешенная

- средняя арифметическая простая

где У_i - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

n- число наблюдение;

f_i - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

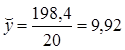
Показатели вариации:

- размах вариации:

R=y_max -y_min

где у_max - максимальное значение признака,

у _min – минимальное значение признака;

R=13,3-6,3=7,0

- среднее линейное отклонение:

,

где у – индивидуальные значения признака,

у – средняя величина,

f– частота;

d=9,86-9,92=0,06

- дисперсия:

;

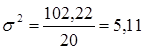
- среднее квадратическое отклонение:

;

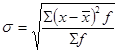- коэффициент вариации:

.

Коэффициент вариации показывает степень однородности совокупности. Так как V < 33% - совокупность однородна.

- коэффициент осцилляции:

V=7,0/9,92*100%=70,56

- линейный коэффициент вариации:

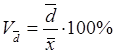
V=0,06/9,92*100%=0,06%

Задача 2

Разделив первые 30 регионов (см. данные из Задания 1) на 2 группы по величине признака, соответствующего вашему варианту, проверьте правило сложения дисперсий.

По результатам расчетов сделать вывод.

Методика решения

Межгрупповая дисперсия характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних , от общей средней :

,

где f — численность единиц в группе.

Внутригрупповая (частная) дисперсия отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы , (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:

;

.

На основании внутригрупповой дисперсии по каждой группе, т.е. на основании можно определить среднюю из внутригрупповых дисперсий:

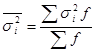
Согласно правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

Ход расчета дисперсий:

1)определяем значения дисперсий по каждой группе (внутригрупповые дисперсии);

у² =У(y-y_i )² f/ Уf

у₁ ² =5024830,6/6=837471,76 у₁ ² =51/6=8,5

у₂ ² =4870450,2/2=2435225,1 у₂ ² =4,62/2=2,31

у₃ ² =4718478,2/2=2359239,1 у₃ ² =2,5/2=1,25

у₄ ² =4568915,2/7=652702,17 у₄ ² =8,2/5=1,64

у₅ ² =4421760,8/3=1473920,2 у₅ ² =35,9/5=7,18

2) среднее значение дисперсии по двум группам;

у₁₂ ² =118022220=5901,1 у₁₂ ² =102,2220=5,11

3) общую дисперсию по правилу сложения.

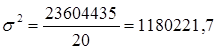
у² =5906,211/20=295,31

Для проверки результатов расчета рассчитываем общую дисперсию, без учета деления регионов на группы.

Задача 3

По группе регионов (см. исходные данные Задания №1) необходимо:

1) найти линейное уравнение парной регрессии между результативным (ВРП) и факторным признаком (х_i ), оценить полученные результаты;

х₁ – потребительские расходы;

х₂ – государственные расходы

х₃ – валовые инвестиции

х₄ – экспорт

х₅ – средняя заработная плата

2) количественно оценить тесноту связи между результативным признаком и факторами.

3) по исходным данным постройте эмпирическую и теоретическую линии регрессии.

4) проверить адекватность модели на основе критерия Фишера и значимость коэффициентов регрессии на основе критерия Стьюдента.

По результатам расчетов сделать вывод.

Таблица 7Варианты заданий

Номерварианта	Регион	xi	Номерварианта	Регион	xi	Номерварианта	Регион	xi
1	с 1 по 20	Х1	11	с 50 по 69	Х1	21	с 32 по 51	Х1
2	с 5 по 24	Х2	12	с 55 по 74	Х2	22	с 28 по 47	Х2
3	с 10 по 29	Х3	13	с 60 по 79	Х3	23	с 81 по 100	Х3
4	с 15 по 34	Х4	14	с 65 по 84	Х4	24	с 76 по 95	Х4
5	с 20 по 39	Х5	15	с 70 по 89	Х5	25	с 61 по 80	Х5
6	с 25 по 44	Х1	16	с 75 по 94	Х1	26	с 51 по 70	Х1
7	с 30 по 49	Х2	17	с 80 по 99	Х2	27	с 41 по 60	Х2
8	с 35 по 54	Х3	18	с 14 по 33	Х3	28	с 21 по 40	Х3
9	с 40 по 59	Х4	19	с 17 по 36	Х4	29	с 3 по 22	Х4
10	с 45 по 64	Х5	20	с 23 по 42	Х5	30	с 54 по 73	Х5

РЕШЕНИЕ

Параметры уравнения парной линейной зависимости а и b

могут быть определены методом наименьших квадратов путем решения системы нормальных уравнений:

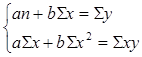
Параметр b - это линейный коэффициент регрессии, характеризующий направление (+b - связь прямая; - b - связь обратная) и силу связи.

Он может быть рассчитан по формуле:

b=60,6 272

b=16483,2 - 332,6/295,31=54,69

Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака у при изменении признака-фактора х на один процент. Для определения коэффициента эластичности используется формула:

Э=54,69*272/60,6=245,47

Подставляя эмпирические значения признака фактора х в уравнение регрессии, определим теоретические значения результативного признака у_x . попуществляется по формулеа, а значимость коэффициентов регрессии на основе критерия Стьюдента

Тесноту связи так же необходимо охарактеризовать линейным коэффициентом корреляции.

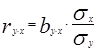или

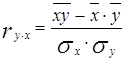
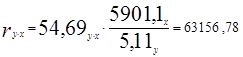
Задача 4

По предприятию имеются следующие данные о реализованной продукции, определите:

- индивидуальные индексы цены, физического объема и товарооборота;

- агрегатный индекс товарооборота, цен и физического объема (показать их взаимосвязь)

- абсолютное изменение товарооборота за счет изменения ассортимента продукции и цены продажи;

- индекс структурных сдвигов, индексы фиксированного и переменного состава, показать их взаимосвязь.

По результатам расчетов сделать вывод.

Значение N определяется по последней цифре номера зачетной книжки студента. N=3

Таблица 9Исходные данные

Продукция	Продано продукции, кг.		Цена 1 кг.
	Базисный период	Текущий период	Базисный период	Текущий период
Кирпич	1000+10*N	800+10*N	45+N	50+N
Шифер	900+10*N	960+10*N	51+N	48+N
Черепица	800+10*N	830+10*N	52+N	54+N
Металл листовой	300+10*N	520+10*N	58+N	60+N

РЕШЕНИЕ

Значение N определяется по последней цифре номера зачетной книжки студента. N=3

Таблица 10Исходные данные

Продукция	Продано продукции, кг.		Цена 1 кг.
	Базисный период	Текущий период	Базисный период	Текущий период
Кирпич	1000+10*3	800+10*3	45+3	50+3
Шифер	900+10*3	960+10*3	51+3	48+3
Черепица	800+10*3	830+10*3	52+3	54+3
Металл листовой	300+10*3	520+10*3	58+3	60+3

Таблица 11Исходные данные

Продукция	Продано продукции, кг.		Цена 1 кг.
	Базисный период	Текущий период	Базисный период	Текущий период
Кирпич	1030	830	48	53
Шифер	930	990	54	51
Черепица	830	860	55	57
Металл листовой	330	550	61	63

Схема расчета индивидуального индекса:

,

где к₁ – индексируемый показатель в отчетном периоде,

к_о – индексируемый показатель в базисном периоде.

Агрегатный индекс товарооборота:

Агрегатный индекс цены:

Агрегатный индекс физического объема:

Индекс переменного состава =

Индекс постоянного состава =

=0,047

Индекс структурных сдвигов =

Задача 5

Из общего количества рабочих предприятия была проведена Х %-я случайная бесповторная выборка с целью определения затрат времени на проезд к месту работы. Результаты выборки представлены в таблице 6 .

Таблица 10

Затраты времени на проезд к месту работы, мин	До 30	30-40	40-50	50-60	60-70
Число рабочих	А	80	В	55	С

Определите:

- доверительный интервал средних затрат времени на проезд к месту, гарантируя результат с вероятностью 0,997;

- долю рабочих предприятия, у которых затраты времени на проезд к месту работы составляют 60 мин. и более, гарантируя результат с вероятностью 0,954

Таблица 11

Вариант	А	В	С	Х	Вариант	А	В	С	Х
1	70	200	45	30	16	90	222	47	10
2	80	210	45	15	17	75	225	49	20
3	90	222	46	10	18	77	230	50	35
4	75	225	47	20	19	79	214	51	5
5	77	230	49	35	20	73	263	52	30
6	79	214	50	5	21	70	210	45	15
7	73	263	51	25	22	80	199	43	10
8	71	210	52	30	23	90	250	46	20
9	70	199	45	15	24	75	231	47	35
10	80	250	43	10	25	77	222	49	5
11	90	231	40	20	26	79	233	50	25
12	75	222	45	35	27	73	200	51	30
13	77	233	45	5	28	90	250	52	15
14	70	200	45	30	29	75	231	45	10
15	80	210	46	15	30	77	222	43	20

РЕШЕНИЕ

Границы генеральной средней определяются как:

,

где - генеральная средняя,

- выборочная средняя,

Д- предельная ошибка выборочной средней:

- при случайной бесповторной выборке:

,

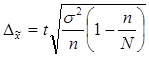где - коэффициент доверия, зависящий от того, с какой вероятностью определяется предельная ошибка:

при р=0,663 t=1,

при р=0,954 t=2,

при p= 0,997 t=3;

n – объем выборочной совокупности,

N – объем генеральной совокупности,

- дисперсия признака выборочной совокупности.

Дx=2

Границы генеральной доли находятся как:

,

где р – генеральная доля,

- выборочная доля (доля рабочих, обладающих указанным признаком):

,

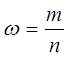где - число единиц, обладающих данным признаком,

n - объем выборочной совокупности.

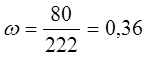
- предельная ошибка доли:

.

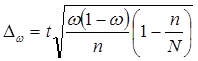=0,758

СПИСОК ЛИТЕРАТУРЫ

1. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учеб. пособие.- 2-е изд. перераб. и доп.- М.: Финансы и статистика, 2003.-336с.

2. Елисеева И.И., Флуд Н.А., Юзбашев М.М. Практикум по общей теории статистики: Учеб. пособие.- М.: Финансы и статистика,2008.- 512с.

3. Общая теория статистики: Учебник./ Под.ред.И.И. Елисеевой. - 5-е изд., перераб. и доп.- М.: Финансы и статистика, 2008.- 656с.

4. Практикум по теории статистики: Учеб. пособие/ Под.ред. Шмойловой Р.А.- 3-е изд..– М.: Финансы и статистика,2008.-416с.

5. Салин В.Н., Чурилова Э.Ю.Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. – М.: Финансы и статистика, 2007. – 480с.

6. Статистика: Учебник / И.И. Елисеева, И.И. Егорова и др.; Под ред. проф. И.И. Елисеевой. – М.: ТК Велби, Изд-во Проспект, 2004

7. Теория статистики: Учебник/ Под.ред. Шмойловой Р.А.- 5-е изд..– М.: Финансы и статистика,2008.- 656с.

8. Материалы сайта Государственного комитета РФ по статистике