Название: Линейное уравнение регрессии
Вид работы: лабораторная работа
Рубрика: Экономика
Размер файла: 306.34 Kb
Скачать файл: referat.me-382669.docx
Краткое описание работы: Составление матрицы парных коэффициентов корреляции переменных. Построение линейного уравнения регрессии, характеризирующее зависимость цены от факторов. Оценка статистической значимости параметров в регрессионной модели с помощью t-критерия Стьюдента.
Линейное уравнение регрессии
Всероссийский заочный финансово-экономический институт
Лабораторная работа
по дисциплине "Эконометрика"
Брянск 2010
Задание
В таблице 1 представлены данные о рынке строящегося жилья в Санкт-Петербурге (по состоянию на декабрь 1996г.).
Таблица 1 – Исходные данные
| № п/п |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
У |
| 1 |
1 |
1 |
39 |
20 |
8,2 |
0 |
1 |
0 |
15,9 |
| 2 |
3 |
1 |
68,4 |
40,5 |
10,7 |
0 |
1 |
0 |
27 |
| 3 |
1 |
1 |
34,8 |
16 |
10,7 |
0 |
1 |
12 |
13,5 |
| 4 |
1 |
1 |
39 |
20 |
8,5 |
0 |
1 |
12 |
15,1 |
| 5 |
2 |
1 |
54,7 |
28 |
10,7 |
0 |
1 |
12 |
21,1 |
| 6 |
3 |
1 |
74,7 |
46,3 |
10,7 |
0 |
1 |
12 |
28,7 |
| 7 |
3 |
1 |
71,7 |
45,9 |
10,7 |
0 |
0 |
0 |
27,2 |
| 8 |
3 |
1 |
74,5 |
47,5 |
10,4 |
0 |
0 |
0 |
28,3 |
| 9 |
4 |
1 |
137,7 |
87,2 |
14,6 |
0 |
1 |
0 |
52,3 |
| 10 |
1 |
1 |
40 |
17,7 |
11 |
1 |
1 |
8 |
22 |
| 11 |
2 |
1 |
53 |
31,1 |
10 |
1 |
1 |
8 |
28 |
| 12 |
3 |
1 |
86 |
48,7 |
14 |
1 |
1 |
8 |
45 |
| 13 |
4 |
1 |
98 |
65,8 |
13 |
1 |
1 |
8 |
51 |
| 14 |
2 |
1 |
62,6 |
21,4 |
11 |
1 |
1 |
0 |
34,4 |
| 15 |
1 |
1 |
45,3 |
20,6 |
10,4 |
1 |
1 |
8 |
24,7 |
| 16 |
2 |
1 |
56,4 |
29,7 |
9,4 |
1 |
1 |
8 |
30,8 |
| 17 |
1 |
1 |
37 |
17,8 |
8,3 |
0 |
1 |
0 |
15,9 |
| 18 |
3 |
1 |
67,5 |
43,5 |
8,3 |
0 |
1 |
0 |
29 |
| 19 |
1 |
1 |
37 |
17,8 |
8,3 |
0 |
1 |
3 |
15,4 |
| 20 |
3 |
1 |
69 |
42,4 |
8,3 |
0 |
1 |
3 |
28,6 |
| 21 |
1 |
1 |
40 |
20 |
8,3 |
0 |
0 |
0 |
15,6 |
| 22 |
3 |
1 |
69,1 |
41,3 |
8,3 |
0 |
1 |
0 |
27,7 |
| 23 |
2 |
1 |
38,1 |
35,4 |
13 |
1 |
1 |
20 |
34,1 |
| 24 |
2 |
1 |
75,3 |
41,4 |
12,1 |
1 |
1 |
20 |
37,7 |
| 25 |
3 |
1 |
83,7 |
48,5 |
12,1 |
1 |
1 |
20 |
41,9 |
| 26 |
1 |
1 |
48,7 |
22,3 |
12,4 |
1 |
1 |
20 |
24,4 |
| 27 |
1 |
1 |
39,9 |
18 |
8,1 |
1 |
0 |
0 |
21,3 |
| 28 |
2 |
1 |
68,6 |
35,5 |
17 |
1 |
1 |
12 |
36,7 |
| 29 |
1 |
1 |
39 |
20 |
9,2 |
1 |
0 |
0 |
21,5 |
| 30 |
2 |
1 |
48,6 |
31 |
8 |
1 |
0 |
0 |
26,4 |
| 31 |
3 |
1 |
98 |
56 |
22 |
1 |
0 |
0 |
53,9 |
| 32 |
2 |
1 |
68,5 |
30,7 |
8,3 |
1 |
1 |
6 |
34,2 |
| 33 |
2 |
1 |
71,1 |
36,2 |
13,3 |
1 |
1 |
6 |
35,6 |
| 34 |
3 |
1 |
68 |
41 |
8 |
1 |
1 |
12 |
34 |
| 35 |
1 |
1 |
38 |
19 |
7,4 |
1 |
1 |
12 |
19 |
| 36 |
2 |
1 |
93,2 |
49,5 |
14 |
1 |
1 |
12 |
46,6 |
| 37 |
3 |
1 |
117 |
55,2 |
25 |
1 |
1 |
12 |
58,5 |
| 38 |
1 |
2 |
42 |
21 |
10,2 |
1 |
0 |
12 |
24,2 |
| 39 |
2 |
2 |
62 |
35 |
11 |
1 |
0 |
12 |
35,7 |
| 40 |
3 |
2 |
89 |
52,3 |
11,5 |
1 |
1 |
12 |
51,2 |
| 41 |
4 |
2 |
132 |
89,6 |
11 |
1 |
1 |
12 |
75,9 |
| 42 |
1 |
2 |
40,8 |
19,2 |
10,1 |
1 |
1 |
6 |
21,2 |
| 43 |
2 |
2 |
59,2 |
31,9 |
11,2 |
1 |
1 |
6 |
30,8 |
| 44 |
3 |
2 |
65,4 |
38,9 |
9,3 |
1 |
1 |
6 |
34 |
| 45 |
2 |
2 |
60,2 |
36,3 |
10,9 |
1 |
1 |
12 |
31,9 |
| 46 |
3 |
2 |
82,2 |
49,7 |
13,8 |
1 |
1 |
12 |
43,6 |
| 47 |
3 |
2 |
98,4 |
52,3 |
15,3 |
1 |
1 |
12 |
52,2 |
| 48 |
3 |
3 |
76,7 |
44,7 |
8 |
1 |
1 |
0 |
43,1 |
| 49 |
1 |
3 |
38,7 |
20 |
10,2 |
1 |
1 |
6 |
25 |
| 50 |
2 |
3 |
56,4 |
32,7 |
10,1 |
1 |
1 |
6 |
35,2 |
| 51 |
3 |
3 |
76,7 |
44,7 |
8 |
1 |
1 |
6 |
40,8 |
| 52 |
1 |
3 |
38,7 |
20 |
10,2 |
1 |
0 |
0 |
18,2 |
| 53 |
1 |
3 |
41,5 |
20 |
10,2 |
1 |
1 |
0 |
20,1 |
| 54 |
2 |
3 |
48,8 |
28,5 |
8 |
1 |
0 |
0 |
22,7 |
| 55 |
2 |
3 |
57,4 |
33,5 |
10,1 |
1 |
1 |
0 |
27,6 |
| 56 |
3 |
3 |
76,7 |
44,7 |
8 |
1 |
1 |
0 |
36 |
| 57 |
1 |
4 |
37 |
17,5 |
8,3 |
0 |
1 |
7 |
17,8 |
| 58 |
2 |
4 |
54 |
30,5 |
8,3 |
0 |
1 |
7 |
25,9 |
| 59 |
3 |
4 |
68 |
42,5 |
8,3 |
0 |
1 |
7 |
32,6 |
| 60 |
1 |
4 |
40,5 |
16 |
11 |
0 |
1 |
3 |
19,8 |
| 61 |
2 |
4 |
61 |
31 |
11 |
0 |
1 |
3 |
29,9 |
| 62 |
3 |
4 |
80 |
45,6 |
11 |
0 |
1 |
3 |
39,2 |
| 63 |
1 |
3 |
52 |
21,2 |
11,2 |
1 |
1 |
18 |
22,4 |
| 64 |
2 |
3 |
78,1 |
40 |
11,6 |
1 |
1 |
18 |
35,2 |
| 65 |
3 |
3 |
91,6 |
53,8 |
16 |
1 |
0 |
18 |
41,2 |
| 66 |
1 |
4 |
39,9 |
19,3 |
8,4 |
0 |
1 |
6 |
17,8 |
| 67 |
2 |
4 |
56,2 |
31,4 |
11,1 |
0 |
1 |
6 |
25 |
| 68 |
3 |
4 |
79,1 |
42,4 |
15,5 |
0 |
1 |
6 |
35,2 |
| 69 |
4 |
4 |
91,6 |
55,2 |
9,4 |
0 |
1 |
6 |
40,8 |
Принятые в таблице обозначения:
Y – цена квартиры, тыс.долл.;
Х1 – число комнат в квартире;
Х2 – район города (1 – Приморский, Шувалово-Озерки, 2 – Гражданка, 3 – Юго-запад, 4 - Красносельский);
Х3 – общая площадь квартиры (м2 );
Х4 – жилая площадь квартиры (м2 );
Х5 – площадь кухни (м2 );
Х6 – тип дома (1 – кирпичный, 0 - другой);
Х7 – наличие балкона (1 – есть, 0 - нет);
Х8 – число месяцев до окончания срока строительства.
1) Введите фиктивную переменную z, отражающую местоположение квартиры и позволяющую разделить всю совокупность квартир на две группы: квартиры на севере города (Приморский район, Шувалово-Озерки, Гражданка) и на юге города (Юго-запад, Красносельский район).
2) Составьте матрицу парных коэффициентов корреляции исходных переменных. Вместо переменной х2 используйте фиктивную переменную z.
3) Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов в линейной форме. Установите, какие факторы мультиколлинеарны.
4) Постройте модель у = f(х3 , х6 , х7 , х8 , z) в линейной форме. Какие факторы значимо воздействуют на формирование цены квартиры в этой модели?
5) Существует ли разница в ценах на квартиры, расположенных в северной и южной частях Санкт-Петербурга?
6) Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия Стьюдента; нулевую гипотезу о значимости уравнения регрессии проверьте с помощью F-критерия Фишера; оцените качество уравнения регрессии с помощью коэффициента детерминации R2 .
Решение
1) Введем фиктивную переменную Z вместо Х2, отражающую местоположение квартиры и позволяющую разделить всю совокупность квартир на две группы. Первые 47 квартир относятся к северной части города (Приморский район, Шувалово-Озерки, Гражданка), а оставшиеся 22 квартиры относятся к южной части города (Юго-запад, Красносельский район). Составим матрицу парных коэффициентов корреляции исходных переменных.
| Х1 |
Z |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
У |
| 1 |
1 |
39 |
20 |
8,2 |
0 |
1 |
0 |
15,9 |
| 3 |
1 |
68,4 |
40,5 |
10,7 |
0 |
1 |
0 |
27 |
| 1 |
1 |
34,8 |
16 |
10,7 |
0 |
1 |
12 |
13,5 |
| 1 |
1 |
39 |
20 |
8,5 |
0 |
1 |
12 |
15,1 |
| 2 |
1 |
54,7 |
28 |
10,7 |
0 |
1 |
12 |
21,1 |
| 3 |
1 |
74,7 |
46,3 |
10,7 |
0 |
1 |
12 |
28,7 |
| 3 |
1 |
71,7 |
45,9 |
10,7 |
0 |
0 |
0 |
27,2 |
| 3 |
1 |
74,5 |
47,5 |
10,4 |
0 |
0 |
0 |
28,3 |
| 4 |
1 |
137,7 |
87,2 |
14,6 |
0 |
1 |
0 |
52,3 |
| 1 |
1 |
40 |
17,7 |
11 |
1 |
1 |
8 |
22 |
| 2 |
1 |
53 |
31,1 |
10 |
1 |
1 |
8 |
28 |
| 3 |
1 |
86 |
48,7 |
14 |
1 |
1 |
8 |
45 |
| 4 |
1 |
98 |
65,8 |
13 |
1 |
1 |
8 |
51 |
| 2 |
1 |
62,6 |
21,4 |
11 |
1 |
1 |
0 |
34,4 |
| 1 |
1 |
45,3 |
20,6 |
10,4 |
1 |
1 |
8 |
24,7 |
| 2 |
1 |
56,4 |
29,7 |
9,4 |
1 |
1 |
8 |
30,8 |
| 1 |
1 |
37 |
17,8 |
8,3 |
0 |
1 |
0 |
15,9 |
| 3 |
1 |
67,5 |
43,5 |
8,3 |
0 |
1 |
0 |
29 |
| 1 |
1 |
37 |
17,8 |
8,3 |
0 |
1 |
3 |
15,4 |
| 3 |
1 |
69 |
42,4 |
8,3 |
0 |
1 |
3 |
28,6 |
| 1 |
1 |
40 |
20 |
8,3 |
0 |
0 |
0 |
15,6 |
| 3 |
1 |
69,1 |
41,3 |
8,3 |
0 |
1 |
0 |
27,7 |
| 2 |
1 |
38,1 |
35,4 |
13 |
1 |
1 |
20 |
34,1 |
| 2 |
1 |
75,3 |
41,4 |
12,1 |
1 |
1 |
20 |
37,7 |
| 3 |
1 |
83,7 |
48,5 |
12,1 |
1 |
1 |
20 |
41,9 |
| 1 |
1 |
48,7 |
22,3 |
12,4 |
1 |
1 |
20 |
24,4 |
| 1 |
1 |
39,9 |
18 |
8,1 |
1 |
0 |
0 |
21,3 |
| 2 |
1 |
68,6 |
35,5 |
17 |
1 |
1 |
12 |
36,7 |
| 1 |
1 |
39 |
20 |
9,2 |
1 |
0 |
0 |
21,5 |
| 2 |
1 |
48,6 |
31 |
8 |
1 |
0 |
0 |
26,4 |
| 3 |
1 |
98 |
56 |
22 |
1 |
0 |
0 |
53,9 |
| 2 |
1 |
68,5 |
30,7 |
8,3 |
1 |
1 |
6 |
34,2 |
| 2 |
1 |
71,1 |
36,2 |
13,3 |
1 |
1 |
6 |
35,6 |
| 3 |
1 |
68 |
41 |
8 |
1 |
1 |
12 |
34 |
| 1 |
1 |
38 |
19 |
7,4 |
1 |
1 |
12 |
19 |
| 2 |
1 |
93,2 |
49,5 |
14 |
1 |
1 |
12 |
46,6 |
| 3 |
1 |
117 |
55,2 |
25 |
1 |
1 |
12 |
58,5 |
| 1 |
1 |
42 |
21 |
10,2 |
1 |
0 |
12 |
24,2 |
| 2 |
1 |
62 |
35 |
11 |
1 |
0 |
12 |
35,7 |
| 3 |
1 |
89 |
52,3 |
11,5 |
1 |
1 |
12 |
51,2 |
| 4 |
1 |
132 |
89,6 |
11 |
1 |
1 |
12 |
75,9 |
| 1 |
1 |
40,8 |
19,2 |
10,1 |
1 |
1 |
6 |
21,2 |
| 2 |
1 |
59,2 |
31,9 |
11,2 |
1 |
1 |
6 |
30,8 |
| 3 |
1 |
65,4 |
38,9 |
9,3 |
1 |
1 |
6 |
34 |
| 2 |
1 |
60,2 |
36,3 |
10,9 |
1 |
1 |
12 |
31,9 |
| 3 |
1 |
82,2 |
49,7 |
13,8 |
1 |
1 |
12 |
43,6 |
| 3 |
1 |
98,4 |
52,3 |
15,3 |
1 |
1 |
12 |
52,2 |
| 3 |
0 |
76,7 |
44,7 |
8 |
1 |
1 |
0 |
43,1 |
| 1 |
0 |
38,7 |
20 |
10,2 |
1 |
1 |
6 |
25 |
| 2 |
0 |
56,4 |
32,7 |
10,1 |
1 |
1 |
6 |
35,2 |
| 3 |
0 |
76,7 |
44,7 |
8 |
1 |
1 |
6 |
40,8 |
| 1 |
0 |
38,7 |
20 |
10,2 |
1 |
0 |
0 |
18,2 |
| 1 |
0 |
41,5 |
20 |
10,2 |
1 |
1 |
0 |
20,1 |
| 2 |
0 |
48,8 |
28,5 |
8 |
1 |
0 |
0 |
22,7 |
| 2 |
0 |
57,4 |
33,5 |
10,1 |
1 |
1 |
0 |
27,6 |
| 3 |
0 |
76,7 |
44,7 |
8 |
1 |
1 |
0 |
36 |
| 1 |
0 |
37 |
17,5 |
8,3 |
0 |
1 |
7 |
17,8 |
| 2 |
0 |
54 |
30,5 |
8,3 |
0 |
1 |
7 |
25,9 |
| 3 |
0 |
68 |
42,5 |
8,3 |
0 |
1 |
7 |
32,6 |
| 1 |
0 |
40,5 |
16 |
11 |
0 |
1 |
3 |
19,8 |
| 2 |
0 |
61 |
31 |
11 |
0 |
1 |
3 |
29,9 |
| 3 |
0 |
80 |
45,6 |
11 |
0 |
1 |
3 |
39,2 |
| 1 |
0 |
52 |
21,2 |
11,2 |
1 |
1 |
18 |
22,4 |
| 2 |
0 |
78,1 |
40 |
11,6 |
1 |
1 |
18 |
35,2 |
| 3 |
0 |
91,6 |
53,8 |
16 |
1 |
0 |
18 |
41,2 |
| 1 |
0 |
39,9 |
19,3 |
8,4 |
0 |
1 |
6 |
17,8 |
| 2 |
0 |
56,2 |
31,4 |
11,1 |
0 |
1 |
6 |
25 |
| 3 |
0 |
79,1 |
42,4 |
15,5 |
0 |
1 |
6 |
35,2 |
| 4 |
0 |
91,6 |
55,2 |
9,4 |
0 |
1 |
6 |
40,8 |
2) Проведем корреляционный анализ на выявление зависимости Y от представленных факторов в среде "СтатЭксперт".
Протокол корреляционного анализа
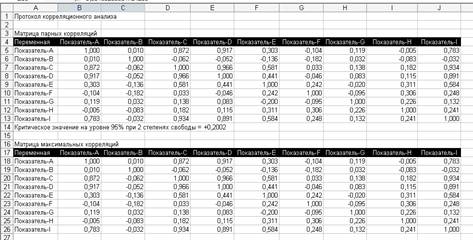
Главная цель анализа данных состоит в выявлении корреляционной связи зависимой переменной Y с независимыми переменными Хi , а также выявление независимых переменных, имеющих высокий уровень корреляции между собой.
Критическое значение коэффициента корреляции rкр = 0,2002. Это означает, что все коэффициенты корреляции, значения которых меньше rкр принимаются равными нулю, а связь между этими параметрами считается незначимой.
Влияние независимой переменной Х3 , Х4 , включенной в исследование, имеет высокий уровень (r > 0,7), причем это влияние положительно (rух3 = 0,872, rух4 = 0,917).
Х5 оказывает умеренное положительное влияние на величину Y (rух5 = 0,303).
Х1 , Х2 , Х6 , Х7 , Х8 не оказывают влияния на величину Y (rух2 = 0,010, rух6 = = -0,104, rух7 = 0,119, rух8 = -0,005).
3) Построим уравнение регрессии, характеризующее зависимость цены от всех факторов, в линейной форме.
Линейная регрессия
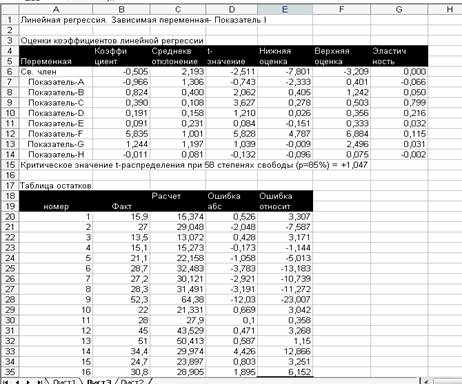
Уравнение будет иметь вид:
у(х) = -0,505 – 0,966х1 + 0,824х2 + 0,390х3 + 0,191х4 + 0,091х5 + 5,835х6 + 1,244х7 – 0,011х8
Линейная или близкая к ней связь между факторами называется мультиколлинеарностью. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,7.
Рассмотрим матрицу парных коэффициентов корреляции между факторами Хj , включенными в дальнейшем анализ.
Матрица парных корреляций
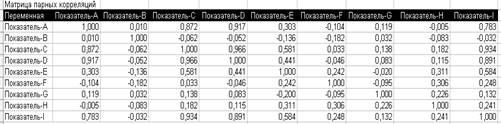
Явление сильной коллинеарности наблюдается между факторами:
Х1 и Х3 , т.к. rх1х3 = 0,872 > 0,7
Х1 и Х4 , т.к. rх1х4 = 0,917 > 0,7
Х3 и Х4 , т.к. rх3х4 = 0,966 > 0,7
4) Построим модель у = f (х3 , х6 , х7 , х8 , z) в линейной форме.
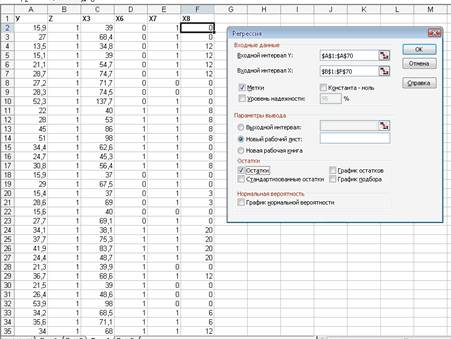
Результаты регрессионного анализа
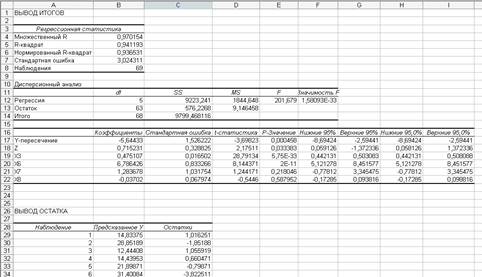
Модель в линейной форме будет иметь вид:
у(х) = -5,64 + 0,715х2 + 0,475х3 + 6,786х6 + 1,284х7 – 0,037х8
Х6 (тип дома), значимо воздействует на формирование цены квартиры в модели.
5) Оценим статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения регрессии проверим с помощью F-критерия; оценим качество уравнения регрессии с помощью коэффициента детерминации R2 .
Характеристика остатков линейной регрессии
| Характеристика |
Значение |
| Среднее значение |
0,000 |
| Дисперсия |
10,579 |
| Приведенная дисперсия |
12,220 |
| Средний модуль остатков |
2,237 |
| Относительная ошибка |
7,144 |
| Критерий Дарбина-Уотсона |
1,154 |
| Коэффициент детерминации |
0,991 |
| F - значение ( n1 = 8, n2 = 58) |
764,697 |
| Критерий адекватности |
36,993 |
| Критерий точности |
47,492 |
| Критерий качества |
44,867 |
| Уравнение значимо с вероятностью 0.95 |
|
Коэффициент детерминации показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 99,1% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
Табличное значение F-критерия (Fкрит ) при доверительной вероятности 0,95 при n1 = 8 и n2 = 58 составляет 2,10. Проверка гипотезы о значимости уравнения регрессии проводится на основании:
если Fфакт > Fкрит , то модель статистически значима;
если Fфакт < Fкрит , то модель статистически незначима.
Fфакт > Fкрит , значит модель статистически значима, т.е. пригодна к использованию.
Оценим с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения регрессии.
Табличное значение t-критерия при 5% уровне значимости и степени свободы k = 69-8-1 = 60 составляет 2,0003.
Если tрасч > tтабл , то коэффициент статистически значим.
Характеристика модели
| Коэффициенты |
Стандартная ошибка |
t-статистика |
|
| Y-пересечение |
-6,10491 |
1,867676003 |
-3,268720937 |
| Переменная Х 1 |
-0,16426 |
1,096321271 |
-0,149825399 |
| Переменная Х 2 |
0,744173 |
0,335026167 |
2,221237839 |
| Переменная Х 3 |
0,36827 |
0,092869614 |
3,965447278 |
| Переменная Х 4 |
0,147869 |
0,132602783 |
1,115126788 |
| Переменная Х 5 |
0,177213 |
0,195399452 |
0,906925347 |
| Переменная Х 6 |
6,93635 |
0,869661345 |
7,975921084 |
| Переменная Х 7 |
1,777648 |
1,124095736 |
1,581402513 |
| Переменная Х 8 |
-0,04802 |
0,072432334 |
-0,662966567 |
tb 0 = 3,2687 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb 1 = 0,1498 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb 2 = 2,2212 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb 3 = 3,9654 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb 4 = 1,1151 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb 5 = 0,9069 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb 6 = 7,9759 > 2,0003 => коэффициент регрессии b0 статистически значим;
tb 7 = 1,5814 < 2,0003 => коэффициент регрессии b0 статистически незначим;
tb 7 = 0,6630 < 2,0003 => коэффициент регрессии b0 статистически незначим;
6) существует ли разница в ценах на квартиры, расположенных в северной и южной частях Санкт-Петербурга?
tb 2 = 2,2212 > 2,0003, tb 3 = 3,9654 > 2,0003 и tb 6 = 7,9759 > 2,0003,
значит факторы Х2 (район города), Х3 (общая площадь квартиры) и Х6 (тип дома) значимо влияют на формирование цен на квартиры.
Анализ показал, что разница в ценах на квартиры, расположенные в северной и южной частях Санкт-Петербурга существенна, т.к. tb 2 = 2,2212 > 2,0003.
Похожие работы
-
Автокорреляция в остатках. Критерий Дарбина-Уотсона
Министерство образования и науки Республики Казахстан Костанайский государственный университет им. А. Байтурсынова Факультет экономический Кафедра информационных систем
-
по Эконометрике
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Кафедра статистики Экономический факультет Контрольная работа по дисциплине: Эконометрика
-
Построение и эконометрический анализ однофакторных регрессионных моделей
Уфимский Государственный Авиационный Технический Университет Кафедра Экономики предпринимательства ОТЧЕТ по лабораторной работе № 1 по дисциплине
-
Рынок вторичного жилья
Исходные данные о продаже квартир на вторичном рынке жилья исследуемого региона, этапы нахождения на данной основе парной регрессии, уравнения линейной регрессии, выборочной дисперсии и ковариации. Определение средней стоимости квартиры, ее вариации.
-
Моделирование экономических показателей
Экономические показатели ( факторы ). Выбор формы представления факторов. Анализ аномальных явлений. Анализ матрицы коэффициентов парных корреляций для абсолютных величин.
-
Линейная регрессия
Расчет параметров уравнения линейной регрессии, экономическая интерпретация регрессии. Определение остаточной суммы квадратов. Выполнение предпосылок МНК. Расчет коэффициента детерминации, проверка значимости уравнения регрессии с помощью критерия Фишера.
-
Анализ данных в линейной регрессионной модели
Построение диаграммы рассеивания (корреляционного поля). Группировка данных и построение корреляционной таблицы. Оценка числовых характеристик для негруппированных и группированных данных. Выборочное значение статистики. Параметры линейной регрессии.
-
Уравнения линейной регрессии, коэффициент регрессии
Федеральное агентство по образованию Всероссийский заочный финансово-экономический институт Контрольная работа по дисциплине «Эконометрика» Архангельск
-
Корреляционно-регрессионный анализ
Этапы корреляционно-регрессионного анализа, построение корреляционной модели и определение функции, отражающей механизм связи между факторным и результативным признаками. Измерение тесноты корреляционной связи, расчет индекса корреляции и дисперсии.
-
Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента
Основные этапы многофакторного корреляционного анализа и интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэффициентов. Расчет значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента.