Referat.me / Экономика / Построение эконометрической модели

Название: Построение эконометрической модели

Вид работы: контрольная работа

Размер файла: 36.93 Kb

Скачать файл: referat.me-397504.docx

Краткое описание работы: Общий вид искомой модели, нахождению структурных коэффициентов. Ранг матрицы системы, число эндогенных переменных, достаточное условие индентифицируемости системы. Применение косвенного метода наименьших квадратов, выражение переменные через отклонения.

Построение эконометрической модели

УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

Кафедра бухгалтерского учета и аудита

Контрольная работа

по дисциплине «Эконометрика»

Исполнитель:

студентка группы ЭУВ 15141 УК

Мурсалимова Э.С.

Проверил:

Касьянов В. А.

Екатеринбург 2006

1. Исходные данные:

год	годовые потребности свинины, кг	оптовая цена за кг, $	доход на душу населения, $	расходы по обработке мяса в %
90	60	5	1300	60
91	62	4	1300	56
92	65	4,2	1500	56
93	62	5	1600	63
94	66	3,8	1800	50

2. Задание.

Построить модель вида:

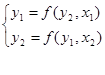
3. Решение.

Общий вид искомой модели:

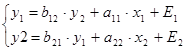a11, a22, b12, b21 – структурные коэффициенты.

Е1, Е2 – погрешность.

Пусть Е1=0 и Е2=0.

Таким образом, решение сводится к нахождению соответствующих структурных коэффициентов a11, a22, b12, b21.

Необходимо отметить, что искомая модель представляет собой систему взаимосвязанных уравнений. Ранг матрицы системы равен максимальному числу линейно – независимых переменных. В нашей системе таковыми являются x1, x2. Достаточным условием индентифицируемости системы является факт, что ранг матрицы системы не менее числа эндогенных переменных системы без единицы. Ранг матрицы равен 2, а число эндогенных переменных также 2 (у1, у2). Соответственно достаточное условие индентифицируемости системы выполняется. В связи с этим, для решения задачи необходимо применять косвенный метод наименьших квадратов.

Составим приведённую форму модели:

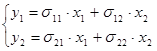
Выразим переменные через отклонения от средних уровней.

y1	y2	х1	х2	y1*x1	x12	x1*x2	y1*x2	x22	y2*x1	y2*x2
-3	0,6	-200	3	600	40000	-600	-9	9	-120	1,8
-1	-0,4	-200	-1	200	40000	200	1	1	80	0,4
2	-0,2	0	-1	0	0	0	-2	1	0	0,2
-1	0,6	100	6	-100	10000	600	-6	36	60	3,6
3	-0,6	300	-7	900	90000	-2100	-21	49	-180	4,2
0	0	0	0	1600	180000	-1900	-37	96	-160	10,2

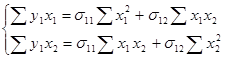
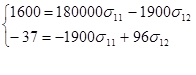
Решим систему в общем виде:

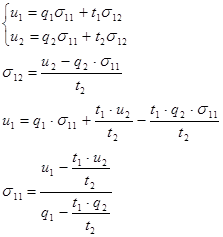
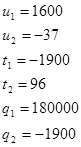
Итак первое уравнение имеет вид:

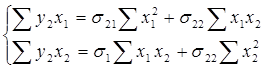
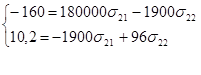
Итак,

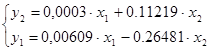
Приведем эту систему к виду

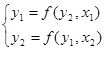
В общем виде:

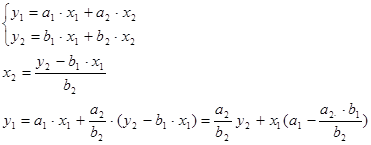
Оба уравнения по структуре одинаковы, следовательно для у2 просто меняем a на b, также при этом меняются индексы.

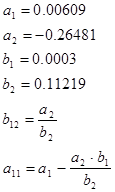
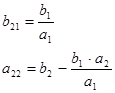
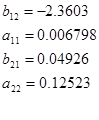
Искомая модель:

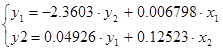
Похожие работы

Матрица анализа возможностей и угроз
Область применения матрицы. Пример вида матрицы. Данные для составления матрицы.
Коллокационная модель прогнозирования количественных характеристик основных финансовых инструментов фондового рынка
Данная работа посвящена вопросу прогнозирования характеристик основных финансовых инструментов фондового рынка при помощи модели средней квадратической коллокации.
по Эконометрике
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Кафедра статистики Экономический факультет Контрольная работа по дисциплине: Эконометрика
Моделирование экономических показателей
Экономические показатели ( факторы ). Выбор формы представления факторов. Анализ аномальных явлений. Анализ матрицы коэффициентов парных корреляций для абсолютных величин.
Корреляционно-регрессионный анализ
Классическая линейную модель множественной регрессии. Значимость уравнения регрессии и его коэффициентов. Доверительный интервал. Матрица парных коэффициентов корреляции. Модель множественной регрессии. Автокорреляция.
Эконометрическая модель Китая
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Государственное образовательное учреждение высшего профессионального образования «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»
Эконометрика. Задачи
1. Раскройте содержание вопроса: суть и содержание гомоскедастичности, Гетероскедастичности остатков; автокорреляции в остатках. Эконометригческие (количественные) выводы и их последующие интерпретация.
Метод наименьших квадратов для однофакторной линейной регрессии
Сущность и применение метода наименьших квадратов для однофакторной линейной регрессии. Нахождение коэффициента эластичности для указанной модели в заданной точке X и его экономический анализ. Прогноз убыточности на основании линейной регрессии.
Линейный множественный регрессионный анализ
Основы линейного регрессионного анализа. Особенности использования функции Кобба-Дугласа. Применение множественной линейной регрессии. Сущность метода наименьших квадратов. Пути избегания ложной корреляции. Проверка значимости коэффициентов регрессии.
Линейная регрессия
Расчет параметров уравнения линейной регрессии, экономическая интерпретация регрессии. Определение остаточной суммы квадратов. Выполнение предпосылок МНК. Расчет коэффициента детерминации, проверка значимости уравнения регрессии с помощью критерия Фишера.