Название: Анализ качества работы системы автоматического регулирования в переходном и установившемся режимах

Вид работы: курсовая работа

Рубрика: Промышленность и производство

Размер файла: 2.7 Mb

Скачать файл: referat.me-299732.docx

Краткое описание работы: Амплитудно и фазо-частотная характеристика разомкнутой системы по передаточным функциям. Переходная характеристика системы по вещественной частотной характеристике замкнутой системы. Качество работы системы в переходном и установившемся режимах.

Анализ качества работы системы автоматического регулирования в переходном и установившемся режимах

Министерство образования и науки Украины

Донбасский Государственный Технический Университет

Кафедра автоматизированных электромеханических систем и электропривода

Анализ качества работы системы автоматического регулирования в переходном и установившемся режимах

Алчевск, 2007

Программа работы

1) Построить логарифмические амплитудно и фазо-частотные характеристики разомкнутой системы по передаточным функциям и их параметрам, взятым из таблицы 1.4 и 1.5

2) Определить запасы устойчивости.

3) Построить вещественную частотную характеристику замкнутой системы по логарифмическим амплитудно и фазо-частотным характеристикам разомкнутой системы.

4) Построить переходную характеристику системы по вещественной частотной характеристике замкнутой системы.

5) Определить показатели качества работы системы в переходном и установившемся режимах.

6) Проанализировать результаты расчетов.

Из таблиц 1.4 и 1.5 выбираем согласно своему варианту следующие данные

,

где Т1=0.8, Т2=0.08, К=2,5

1) Построим ЛАЧХ и ЛФЧХ разомкнутой системы по передаточной функции и их параметрам.

Для данной передаточной функции выполним замену р на j

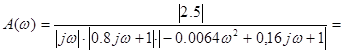
Вычислим логарифмические амплитудно-частотную и фазо-частотную характеристики:

ЛАЧХ и ЛФЧХ изображены на рисунке 1.

Определим частоты сопряжения:

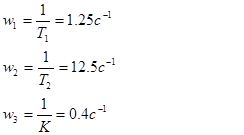
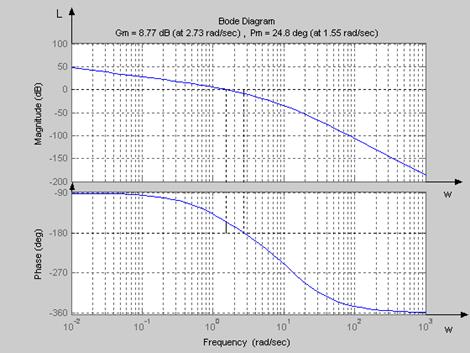
Рисунок 1 - ЛАЧХ и ЛФЧХ разомкнутой системы

2) Определим запасы устойчивости по рисунку 1

8.77 дБ - запас устойчивости по амплитуде;

24.8° - запас устойчивости по фазе;

3) Построить вещественную частотную характеристику замкнутой системы по логарифмическим амплитудно и фазо-частотным характеристикам разомкнутой системы.

ВЧХ замкнутой системы по ЛЧХ разомкнутой системы строиться с помощью специальной номограммы (рисунок 2). Исходными при построении номограммы является выражение

,

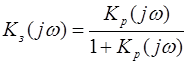Подставляя в это выражение

и ,

Получаем

,

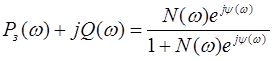откуда видно, что ординаты ВЧХ замкнутой системы связаны с координатами и частотной характеристики разомкнутой системы. Одному и тому же значению соответствуют различные координаты и . Геометрическое место точек на плоскости, где по оси ординат откладываются значения , а по оси абсцисс - значение , соответствующее постоянному значению ординаты ВЧХ , представляет собой определенную кривую. Семейство таких кривых, соответствующих различным значениям , образуют номограмму (рисунок 2), с помощью которой можно определить ВЧХ замкнутой системы по ее ЛЧХ в разомкнутом состоянии.

Для определения ВЧХ замкнутой системы предварительно на номограмме строят ЛАФЧХ разомкнутой системы.

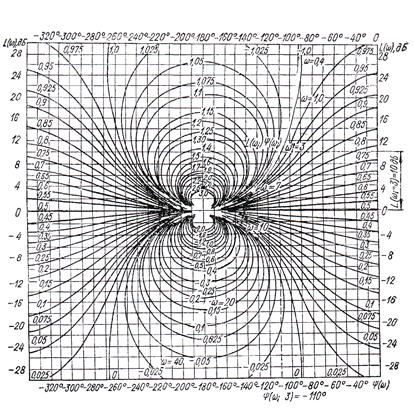
Рисунок 2 - Номограммы с нанесенной ЛАФЧХ разомкнутой системы

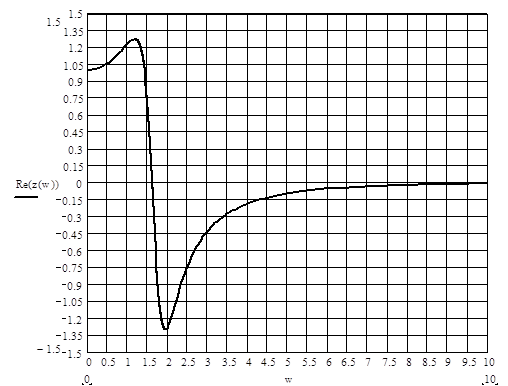
Рисунок 3 - ВЧХ замкнутой системы

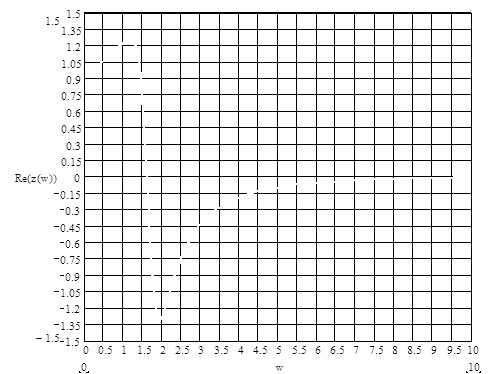
Рисунок 4 - Разложение ВЧХ на прямоугольные трапецеидальные характеристики

4) Построим переходную характеристику системы по вещественной частотной характеристике замкнутой системы.

Заменяем кривую ВЧХ ломаной абвгде (рисунок 3) и в соответствии с последней разбиваем ВЧХ на три прямоугольные трапеции (рисунок 4).

Для оценки качества САУ прибегают к построению кривой переходного процесса системы h (t) [x (t)].

Определим для каждой трапеции:

начальную ординату трапеции Р (0);

частоту положительности ω_{п i} ;

частоту, определяющую длину горизонтального участка ω_{а i} ;

коэффициент наклона χ_i = ω_{а i} /ω_{п i}

Снятые данные с трапеций (рисунок 4):

Р_I (0) =2.64 ω_{а I} =1.41 с^-1 ω_{п I} = 1.83с^-1 χ_I =0.77

Р_II (0) =-1.32 ω_а2 =2.04с^-1 ω_п2 =3.08с^-1 χ₂ =0.66

Р_III (0) =-0.12 ω_а3 =4.4 с^-1 ω_п3 =6.75с^-1 χ₃ =0.65

Из таблицы А7 (Л4) выбираем h- функции с коэффициентом наклона χ, ближайшим к расчётным значениям.

Переходные функции h_i (t) для реальных трапеций находим умножением нормированных ординат h_i на высоту трапеции:

h_i = Р_i (0)

и делением безразмерного времени на частоту w₀ :

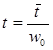
В соответствии с расчетами, приведенными в таблице 1, выполняем построение графиков переходных процессов h₁ (t), h₂ (t), h₃ (t). Графики переходных процессов h₁ (t), h₂ (t), h₃ (t) и h (t) приведены на рисунке 5.

Таблица 1 - Сводная таблица данных для построения переходных функций, соответствующих прямоугольным трапециям.

Трапеция 1	РI (0) =2.64 ωа I =1.41 с-1 ωп I = 1.83с-1 χI =0.77
	0.5	1	2	3.5	6	8	10.5	15.5	20	25
h	0.267	0.519	0.919	1.161	0.984	0.932	1.033	0,983	1,003	1,001
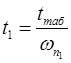	0.273	0.546	1.093	1.912	3.278	4.372	5.737	8.469	10.928	13.662
	0.705	1.371	2.426	3.065	2.597	2.461	2.727	2.595	2.648	2.643
Трапеция 2	РII (0) =-1.32 ωа2 =2.04с-1 ωп2 =3.08с-1 χ2 =0.66
	0.5	1	2	3.5	6	8	10.5	15.5	20	25
h	0.259	0.505	0.899	1.158	1.003	0.935	1.017	0.993	0.995	1.003
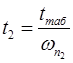	0.163	0.325	0.649	1.136	1.948	2.597	3.409	5.033	6.494	8.117
	-0.342	-0.666	-1.186	-1.528	-1.324	-1.234	-1.342	-1.311	-1.314	-1.324
Трапеция 3	РIII (0) =-0.12 ωа3 =4.4 с-1 ωп3 =6.75с-1 χ3 =0.65
	0.5	1	2	3.5	6	8	10.5	15.5	20	25
h	0.259	0.505	0.899	1.158	1.003	0.935	1.017	0.993	0.995	1.003
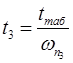	0.074	0.148	0.296	0.518	0.888	1.185	1.555	2.296	2.963	3.703
	-0.032	-0.061	-0.108	-0.121	-0.121	-0.112	-0.123	-0.119	-0.119	-0.121

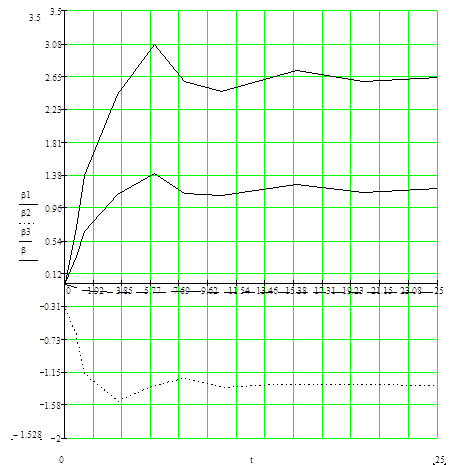
Рисунок 5 - Переходная функция следящей системы и ее составляющей

5) Определить показатели качества работы системы в переходном и установившемся режимах.

Показатели качества работы системы, оценивают по ее переходной функции (рисунок 5). Основными показателями качества являются:

1) максимальное перерегулирование

;

2) длительность переходного процесса (время регулирования)

3) время установления

4) число колебаний N - число колебаний регулируемой величины за время переходного регулирования;

N=1

5) собственная частота колебаний системы

6) степень демпфирования

;

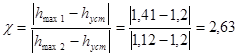Анализ результатов расчёта

В ходе выполнения данного домашнего задания выяснилось, что система является устойчивой. Определили запасы устойчивости системы по амплитуде ΔL=8,77 дБ и по фазе γ=24,8°. Полученные значения являются приемлемыми.

В результате исследования системы были получены значения основных параметров качества переходного процесса, которые лежат в обще допустимых пределах.

Для улучшения динамических свойств данной САУ следует провести её стабилизацию и коррекцию, с помощью дополнительных конструктивных элементов. Однако синтез КУ - это задача и цель домашнего задания №4.

Литература

1. Теория автоматического управления. / Под ред. А.В. Нетушила. - М.: ВШ., 1976, - 400с

2. Зайцев Г.Ф. Теория автоматического управления и регулирования. - К.: ВШ., 1988, - 430с.

3. Лукас В.А. Теория автоматического управления. Учебн. для вузов, - М.: Надра, 1990. - 416с

4. Методические указания к домашним заданиям по курсу "ТАУ"/ Сост.: Сергиенко Н.Н. - Алчевск: ДГМИ, 2003. - 54с.

5. Расчёт автоматических систем. Под ред. А.В. Фатеева. Учебн. пособие для вузов. М., "ВШ", 1973. - 336с.