Название: Расчет структурной схемы системы автоматического управления
Вид работы: курсовая работа
Рубрика: Промышленность и производство
Размер файла: 666.96 Kb
Скачать файл: referat.me-301413.docx
Краткое описание работы: Определение передаточной функции разомкнутой системы, стандартной формы ее записи и степени астатизма. Исследование амплитудно-фазовой, вещественной и мнимой частотных характеристик. Построение годографа АФЧХ. Алгебраические критерии Рауса и Гурвица.
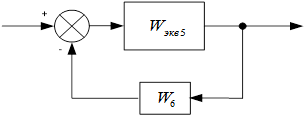
Расчет структурной схемы системы автоматического управления
КУРСОВАЯ РАБОТА
по дисциплине:"Теория автоматического управления"
Уфа 2011
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант 16
| Схема | k1 | k2 | k3 | k4 | k5 | T1 | T2 | T3 | T4 | T5 | ξ |
| (а) | 4 | 1.5 | 4 | 2 | 0.7 | 0.4 | 0.3 | 0.5 | 0.15 | 0.9 | 0.5 |
Схема а:

Для структурной схемы САУ, соответствующей выбранному варианту, выполнить следующие действия:
1) Определить передаточную функцию разомкнутой системы, привести ее к стандартной форме записи. Определить степень астатизма системы.
2) Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики.
3) Построить годограф АФЧХ разомкнутой системы.
4) Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы.
5) Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы.
6) Определить устойчивость замкнутой САР с помощью критерия Найквиста и логарифмических частотных характеристик.
7) Найти запасы устойчивости системы по фазе и амплитуде.
8) Записать выражение для передаточной функции замкнутой системы и проверить выводы пункта 6 с помощью алгебраических критериев Рауса и Гурвица.
9) Проверить выводы пункта 6 с помощью частотного критерия Михайлова.
10) Найти коэффициенты С0 , С1 , С2 ошибок системы.
11) Построить с помощью ЭВМ переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование, и время регулирования) в системе.
передаточный астатизм амплитудный голограф
1. Передаточная функция разомкнутой системы
Упростим схему.
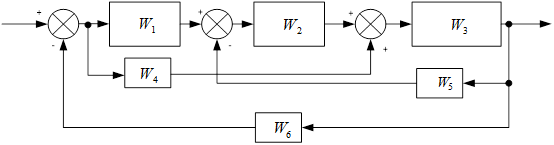
Где
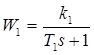 ;
; 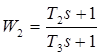 ;
; 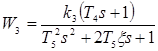 ;
; ![]() ;
; ![]() ;
; ![]() .
.
Перенесем сумматор.
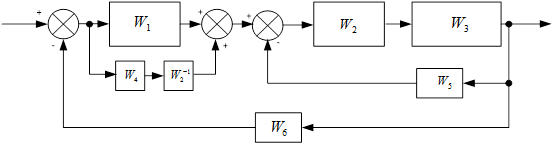
Затем упростим.
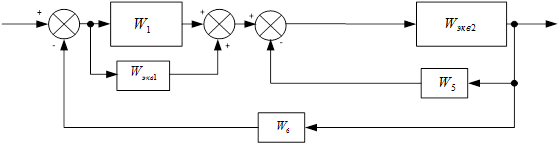
Где
![]() ;
; ![]()
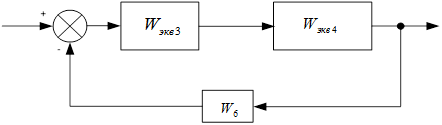
Где
![]() ;
; 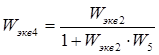
Где
![]()
![]() ;
;
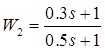 ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;
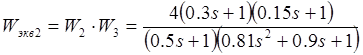 ;
;
![]()
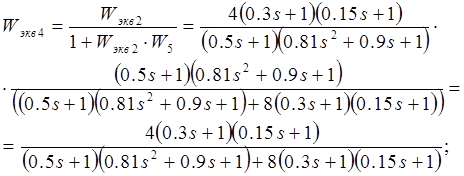
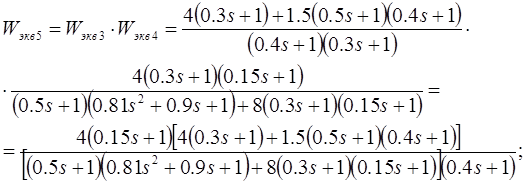
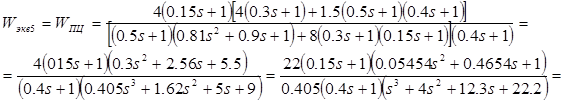
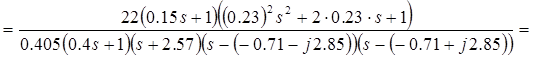
![]()
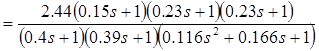
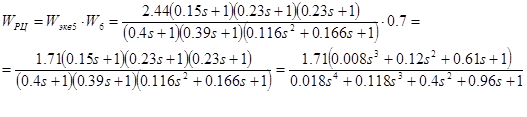
Степень астатизма ν=0. Коэффициент передачи К=1.71. Постоянные времени: Т1 =0.15, Т2 =0.23, Т3 =0.23, Т4 =0.4, Т5 =0.39, Т6 =0.34, ξ=0.24.
2. Частотная передаточная функция системы (s→jω)
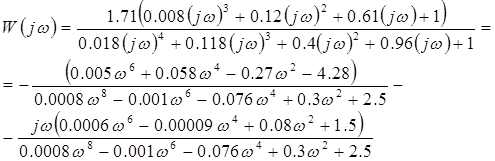
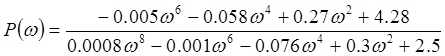
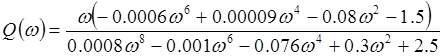
Особые точки АФЧХ приведены в таблице 1.
Таблица 1.
| ω | 0 | 2,85 | ∞ |
| P(ω) | 1.71 | 0 | 0 |
| Q(ω) | 0 | -2.46 | 0 |
3. Годограф АФЧХ разомкнутой системы
Годограф (рисунок 1) при ω=0 начинается на положительной вещественной полуоси. При ω→ ∞ через четвертый и третий квадранты стремиться к нулю. Пересекает при ω=0 вещественную ось в точке (1,71;j0) и при ω=2,85 пересекает мнимую ось в точке (0;-j2.46).
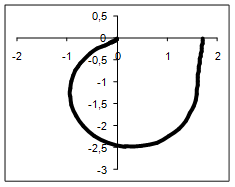
Рисунок 1.
4. Асимптотическая ЛАХ и ЛФХ
Асимптотическая ЛАХ:
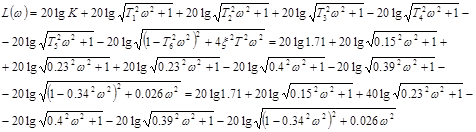
Асимптотическая ЛФХ:
![]()
![]()
5. Построение в масштабе ЛАХ и ЛФХ системы
1) Значение ЛАХ при ω =1 равно 20lgK, где К – коэффициент передачи разомкнутой системы. К=1,71, значит ЛАХ пересекает ось L(ω) на уровне 4.66.
2) Степень астатизма системы ν =0, следовательно наклон самой низкочастотной асимптоты равен 0 дБ/дек.
3) Таблица значений сопрягаемых частот.
Таблица 2.
| Т | 0.4 | 0.39 | 0.34 | 0.23 | 0.23 | 0.15 |
| ω | 2.5 | 2.56 | 2.94 | 4.35 | 4.35 | 6.67 |
| Изменение наклона (дБ/дек) | -20 | -20 | -40 | +20 | +20 | +20 |
Асимптотическая ЛАХ, построенная от руки (схематично) по информации из таблицы 2 показана на рисунке 2.
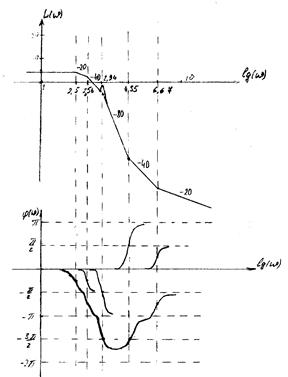
Рисунок 2.
На рисунке 3 показаны в масштабе ЛАХ и ЛФХ системы, построенные с помощью ЭВМ.
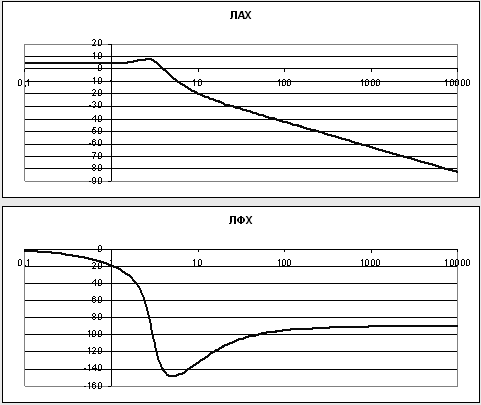
Рисунок 3.
6. Устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик
Степень астатизма системы ν=0 и характеристический полином разомкнутой системы имеет все корни в левой половине комплексной плоскости, то критерий Найквиста будет следующим: Для того чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики разомкнутой системы не охватывал точку с координатами (-1; j0).
На рисунке 4 изображен годограф АФХ. Он не охватывает точку (-1; j0), следовательно, замкнутая система будет устойчивой.
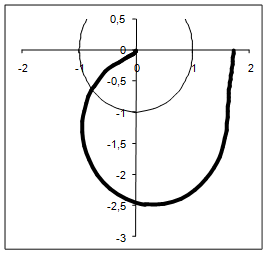
Рисунок 4.
7. Запасы устойчивости по фазе и амплитуде
Как видно из рисунка 4 годограф не пересекает отрицательную вещественную полуось, следовательно, запас устойчивости по амплитуде 100%.
Рассчитаем запас устойчивости по фазе:
Найдем ωср (частоту среза) из условия A(ω)=1
![]()
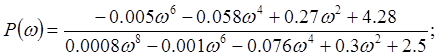
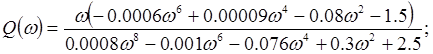
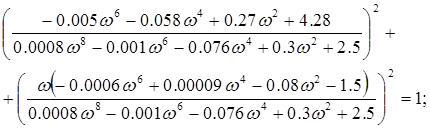
ωср =3,924 с-1
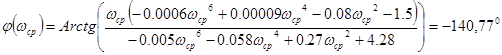
![]()
Таким образом запас по фазе составляет 39,230 .
Передаточная функция замкнутой системы может быть найдена по следующей формуле
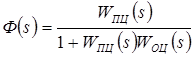
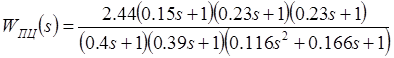
![]()
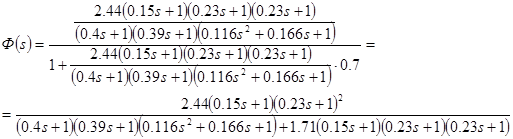
Характеристический полином системы:
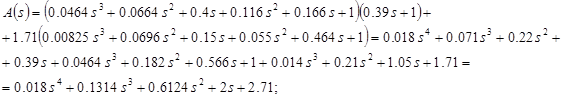
![]()
Определение устойчивости замкнутой системы методом Рауса.
![]()
Таблица Рауса.
| a0 | a2 | a4 | |
| a1 | a3 | a5 =0 | |
| C13 =a2 -τ3 a3 | C23 =a4 -τ3 a5 | C33 =a6 -τ3 a7 | τ 3 =a0 /a1 |
| C14 =a3 - τ4 C23 | C24 =a5 - τ4 C33 | C34 =0 | τ 4 =a1 /C13 |
| C15 =C23 -τ5 C24 | C25 =C33 -τ5 C34 | C35 =0 | τ 5 =C13 /C14 |
| C16 =C24 -τ6 C25 | C26 =C34 -τ6 C35 | C36 =0 | τ 6 =C14 /C15 |
Заполним таблицу.
| 0.018 | 0.612 | 2.71 | |
| 0.1314 | 2 | 0 | |
| C13 =0.3384 | C23 =2.71 | C33 =0 | τ 3 =0.137 |
| C14 =0.948 | C24 =0 | C34 =0 | τ 4 =0.388 |
| C15 =2.71 | C25 =0 | C35 =0 | τ 5 =0.357 |
| C16 =0 | C26 =0 | C36 =0 | τ 6 =0.34 |
Все элементы первого столбца таблицы имеют один и тот же знак, следовательно, характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.
Определение устойчивости замкнутой системы методом Гурвица.
Построим определители Гурвица
![]()
![]()
![]()
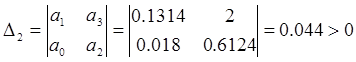
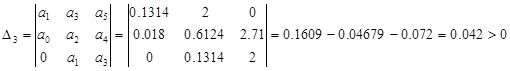
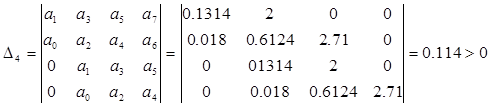
Все определители Гурвица положительны, следовательно, характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.
8. Определение устойчивости замкнутой системы с помощью частотного критерия Михайлова
Характеристический полином системы
![]()
s→jω
![]()
Вещественная функция Михайлова:
![]() .
.
Мнимая функция Михайлова:
![]()
Решим уравнения
![]() ;
;![]() .
.
![]() ,
,
Учитываем корни ω > 0
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Построим таблицу
| ω | 0 | 2.88 | 3.9 | 5.36 |
| Re(ω) | 2.71 | 0 | -2.44 | 0 |
| Im(ω) | 0 | 3 | 0 | -9.57 |
Годограф Михайлова (в схематичном виде) представлен на рисунке 5.
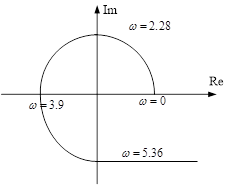
Рисунок 5.
Критерий Михайлова: Замкнутая САУ будет устойчивой тогда и только тогда, когда годограф Михайлова, при изменении частоты ω от 0 до +∞ начинаясь на положительной действительной полуоси последовательно и нигде не обращаясь в 0 пересекает n квадрантов комплексной плоскости (где n – порядок характеристического полинома САУ).
В данном случае годограф соответствует критерию Михайлова, значит замкнутая САУ устойчива.
9. Коэффициенты ошибок системы
Передаточная функция ошибки будет иметь вид
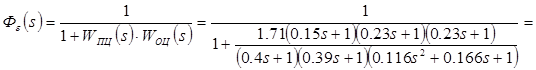
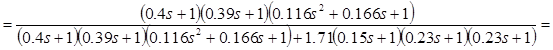
![]()
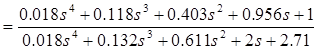
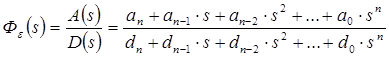
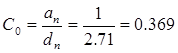
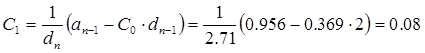
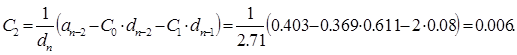
10. Переходная функция САУ
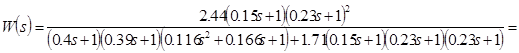
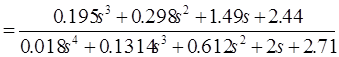
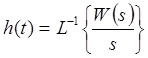
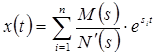
![]()
![]()
![]()
Найдем корни N(s):
![]()
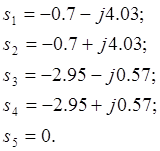
Получим следующее:
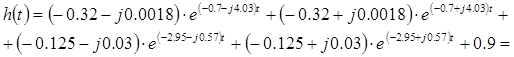
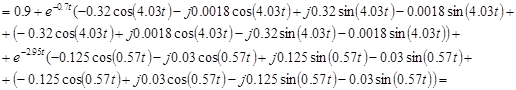
![]()
Построим график с помощью ЭВМ.
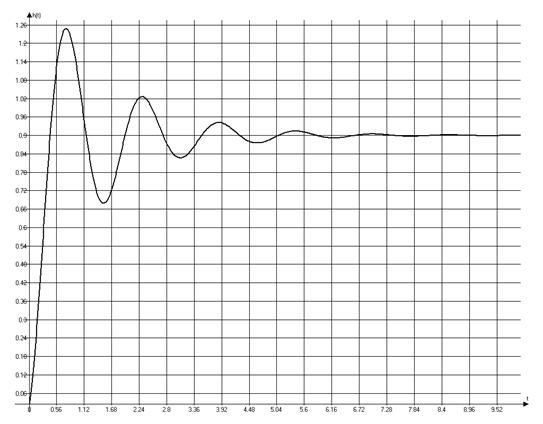
График переходной функции.
Из графика видно, что время регулирования tp ≈3.29с, а перерегулирование
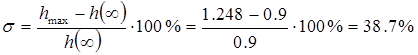 .
.
Похожие работы
-
Система стабилизации скорости подачи лесопильной рамы
Контрольная работа №1А. «Система стабилизации скорости подачи лесопильной рамы». Задание 1. Для контура, соответствующего варианту задания, начертить функциональную схему системы автоматического регулирования. Описать принцип ее действия. Определить из каких динамических звеньев состоит исследуемая САР.
-
Анализ САУ с помощью MATLAB и SIMULINK
Построение временных характеристик с помощью пакета Control System В качестве примера выберем апериодическое звено первого порядка Для построения временных характеристик с помощью пакета Control System используются функции step и impulse.
-
Исследование систем автоматического управления (САУ)
Основные свойства, функциональное назначение, принцип действия, структурная схема САУ, а также дифференциальные уравнения и передаточные функции ее элементов. Анализ и оценка устойчивости замкнутой САУ. Синтез последовательного корректирующего устройства.
-
Устойчивость систем автоматического управления
Характеристика устойчивости системы стабилизации угла тангажа самолета, ее роль. Определение критического значения передаточного числа автопилота по углу тангажа, используя различные критериями устойчивости: Рауса-Гурвица, Михайлова и Найквиста.
-
Расчет системы автоматического управления
Расчет и структурная схема передаточных функций разомкнутой и замкнутой системы автоматического управления (САУ) относительно входного воздействия. Формулы для мнимой и вещественной компоненты. Графики логарифмических амплитудной и фазовой характеристик.
-
Система автоматического регулирования давления в ресивере
Построение структурной схемы нескорректированной системы и определение передаточных функций звеньев. Построение логарифмических амплитудно-частотных характеристик для исходной системы. Синтез и моделирование последовательного корректирующего устройства.
-
Критерии устойчивости систем
Методика определения устойчивости системы по алгебраическим (критерии Рауса и Гурвица) и частотным критериям устойчивости (критерии Михайлова и Найквиста), оценка точности их результатов. Особенности составления передаточной функции для замкнутой системы.
-
Анализ качества работы системы автоматического регулирования в переходном и установившемся режимах
Амплитудно и фазо-частотная характеристика разомкнутой системы по передаточным функциям. Переходная характеристика системы по вещественной частотной характеристике замкнутой системы. Качество работы системы в переходном и установившемся режимах.
-
Анализ системы автоматического регулирования угловой скорости вращения турбины
Определение передаточной функции разомкнутой, замкнутой систем и передаточной функции по ошибке. Определение запасов устойчивости. Определить параметры корректирующего звена, обеспечивающие наибольшее быстродействие при достаточном запасе устойчивости.
-
Анализ системы автоматического регулирования температуры теплоносителя в агрегате АВМ
Устройство, особенности работы, функциональная схема и анализ системы автоматического регулирования температуры теплоносителя в агрегате витаминизированной муки (АВМ). Оценка зависимости статической ошибки от изменения управляющего воздействия на АВМ.