Название: Расчёт на прочность жёсткость и проектирование бруса в условиях сложного сопротивления статическому
Вид работы: курсовая работа
Рубрика: Промышленность и производство
Размер файла: 383.83 Kb
Скачать файл: referat.me-301800.docx
Краткое описание работы: Курсовая работа по сопротивлению материалов "Расчёт на прочность, жёсткость и проектирование бруса в условиях сложного сопротивления статическому и динамическому нагружению"
Расчёт на прочность жёсткость и проектирование бруса в условиях сложного сопротивления статическому
Курсовая работа по сопротивлению материалов
"Расчёт на прочность, жёсткость и проектирование бруса в условиях сложного сопротивления статическому и динамическому нагружению"
1. Напряженное и деформированное состояние в опасной точке, проверка прочности
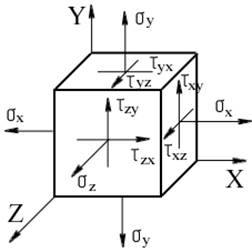
1.1 Определение главных напряжений в опасной точке и проверка
|
| σx , МПа | σy , МПа | σz , МПа | τxy , МПа | τzy , МПа | τxz , МПа |
| 350 | -310 | 420 | 0 | 350 | 100 |
|
|
|
|
 |
|
|
|
Инварианты напряженного состояния по заданным компонентам
I 1 = σ x +σ y +σ z =460
I 2 = σ y ּσ z +σ z ּσ x +σ x ּσ y -τ xy 2 -τ zy 2 -τ xz 2 = -224200
σ x τ xy τ xz
I 3 =τ xy σ y τ zy = (σ x ּσ y ּσ z + τ xy ּτ zy ּτ xz + τ xy ּτ zy ּτ xz )- (τ xz ּσ y ּτ xz +τ xy ּτ xy ּσ z +τ zy ּτ zy ּσ x )
τ xz τ zy σ z =-85345000
Нахождение главных напряжений решением кубического уравнения
σ k 3 – σ k 2 ּI 1 + σ k ּI 2 – I 3 = 0
σ k 3 – σ k 2 ּ4 60 – σ k ּ224200 – 85345000 = 0
Приводим уравнение к каноническому виду
q
= 
=
21878796,29
p
= 
=
-98244,45
r
= 
=
313,44
(
т
.
к
.
q
> 0)
= 
=
0,7105
=
44,72
˚
=
14,9
˚
y
1
= 
= -605,8
y
2
=
=
442,49
y
3
=
= 163,31
σ1
=
=
-452,4
σ2
=
=
595,82
σ3
=
=
316,64
σ1
>σ2
>σ3
σ1
=
-452,4; σ2
= 595,82; σ3
= 316,64
Проверка
I 1г = σ 1 + σ 2 + σ 3 = 460
I 2 г = σ1 ּσ2 +σ1 ּσ3 +σ2 ּσ3 = -224200
I 3 г = σ1 ּσ2 ּσ3 = -85345000
Δ I1 = (I1 г – I1 )/ I1 =0
Δ I2 = (I2 г – I2 )/ I2 =0
Δ I 3 = ( I 3г – I 3 )/ I 3 =0
1.2 Проверка прочности
Условие прочности:
n
> [
n
]
n
=
[
n
] =
Материал 12ХН3А
σ Т =700 МПа
σ В =950 МПа
[
n
] =
= 1,74
n
=
= 1,279
n
< [
n
] условие прочности не выполняется.
2. Компоненты тензора напряжений и проверка прочности в простейших случаях сопротивления бруса
2.1. Расчет на прочность конструкций типа кронштейнов, подвесок, валов, элементы которых работают на равномерное растяжение, сжатие
2.1.1 Силовая задача
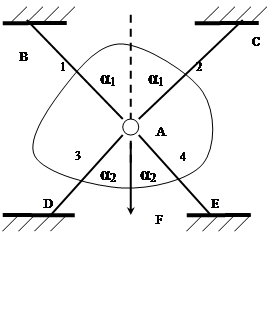
l 1 = l 2 = 24 см
l 3 = l 4 =31 см
A 1 = A 2 = 2,5 см2
A3 = A4 = 2 см 2
F= 120 КН
α1 =53°
α2 =40°
Материал – 12ХНЗА
2.1.2 Определение статической неопределимости
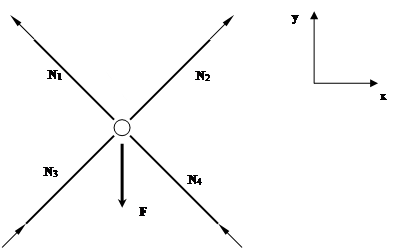
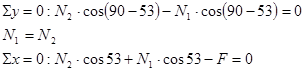
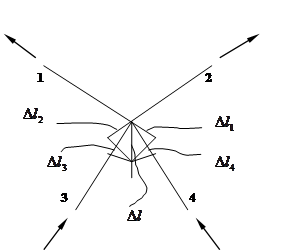
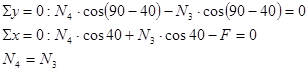
2.1.3 Уравнение деформации
Используя закон Гука имеем:
;
; 
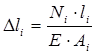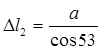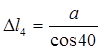
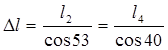
2.1.4 Определение внутренних усилий
;
;
;
;
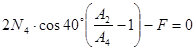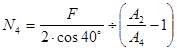N 4 =313,3 кН;
кН
N 1 = N 2 = 99,69 кН
N 3 = N 4 = 313,3 кН.
2.1. 5 Нахождение напряжений в стержнях
2.1.6 Проверка прочности
Условие прочности:
n
>[
n
]
n
=
[
n
] =
[
n
] =
= 1,74
n
=
= 4,47 МПа
n
> [
n
] условие прочности выполняется
2.2 Расчет на прочность и жесткость конструкций типа валов, осей, работающих на кручение
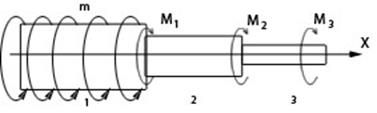
M 1 = -30 кН·м
M 2 = -25 кН·м
M 3 = 10 кН·м
К D 1 = 6.5
К D 2 = 6.0
К D 3 = 2,5
К d 1 = 5.5
К d 2 = 5.5
К d 3 = 2.0
l 1 = 0,65 м; l 2 = 0,5 м; l 3 = 0,45 м
Материал – Ст. 45; 
= 360МПа; 
= 610 МПа;
G
= 80 ГПа
2.2.1 Определение величины реактивного погонного момента
;m
= -69,23 кН·м
2.2.2 Система в данном случае статически определена
Рассмотрим 3 участка
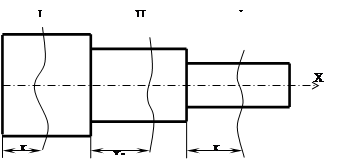
I) 
= –
m
·
x
1
= 69,23·
x
1
x 1 =0; M кр1 =0
x 1 = l 1 =0.65; M кр1 = 45 КН·м
II
)
M кр2 = M 1 - m · l 1 = -30 – (– 45) = 15 КН·м
III
)
M кр3 = M 1 + M 2 – m · l 1 = – 30 – 25 – (-45) = -10 КН·м
2.2.3 Определение опасного сечения
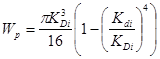
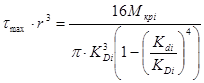
участок №1
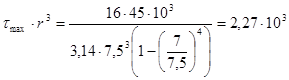
участок №2
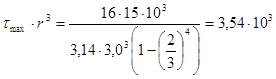
участок №3
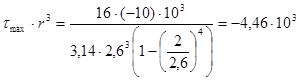
2.2.4 Определение геометрического параметра r , Di и di из условия прочности в опасном сечении
[n] = = 
[
σ
] = 
=
[
]=113.2
МПа
r3
= 
=
r = 
Di = KDi ·r
D 1 = 0,204 м
D 2 = 0,0816 м
D 3 = 0,0707 м
di = Kdi ·к
d 1 = 0,19 м
d 2 = 0,054 м
d 3 = 0,054 м
2.2.5 Определение значений 
в различных сечениях бруса
76,4 МПа
113,3 МПа
144,3 МПа
2.2.6 Определение погонного углов закручивания θ и φ
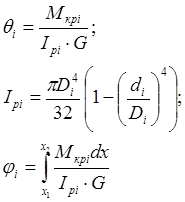
Ip1
= 
м
4
Ip2
= 
м
4
Ip3
= 
м
4
θ
1
= 
рад
/
м
θ
2
= 
рад
/
м
θ
3
= 
рад
/
м
φ1
=
=
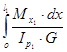θ1
·
x
= 
φ2
=
=
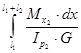φ1
+θ2
·
x
= 
φ3
= φ2
+θ3
·
x
=
Условие жесткости по
условие жесткости выполняется
|
3.Прочность и проектирование бруса, работающего при плоском поперечном прямом изгибе
3.1 Проектирование и расчет на прочность «оптимальной» балки с составным поперечным сечением
l 1 = l 3 = 1,6 м F = 35 кН М = 60 кНм
l 2 = 1,8 м q = 35 кН/м
3.1.1 Построение эпюры перерезывающих (поперечных) сил и изгибающих моментов
1) 0 ≤ x ≤ l 3
2) l 3 ≤ x ≤ l 3 + l 2
КН
КН
КН·м
КН·м
3) l 3 + l 2 ≤ x ≤ l 3 + l 2 + l 1
КН
КН
КН
·
м
КН
·
м
3.2 Определение параметров поперечного сечения тонкостенной балки и полная проверка прочности
| L1 | L2 | L3 | F | q | M | Материал ВТ-3 |
| м | м | м | кН | кН/м | кН·м | σТ = 850 МПа |
| 1,4 | 1,2 | 1,4 | 20 | 55 | 15 | σВ = 950 МПа |
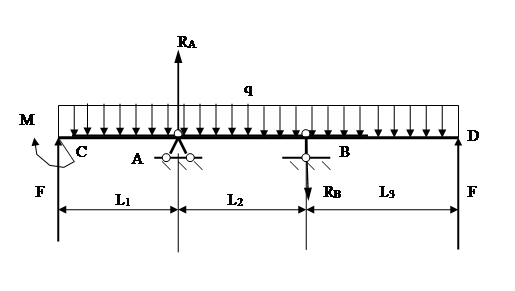
3.2.1 Определение опорных реакций
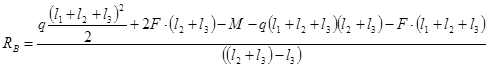
3.2.2. Построение эпюр перерезывающих сил (поперечных) и изгибающих моментов:
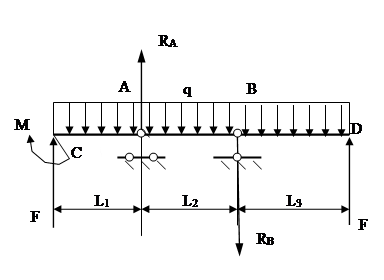
1) 0 ≤ x ≤ l 1
2) l 1 ≤ x ≤ l 1 + l 2
3) 0≤ x ≤ l 3
3.2.3 Определение координаты опасного сечения, как сечения, в котором изгибающий момент достигает максимальной величины
Mzmax =25,9 КН·м в точке с координатой x = l 3 – опасное сечение
3.2.4 Определение величины параметра t из условия прочности по переменным напряжениям
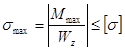
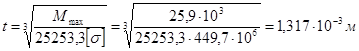
3.2.5 Определение максимального касательного напряжения в сечении, в котором перерезывающая сила достигает наибольшей величины
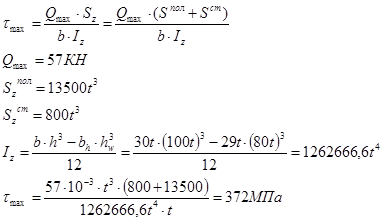
3.2. 6 Проверка прочности по касательным напряжениям
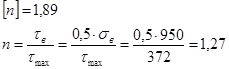
n <[ n ] – условие прочности не выполняется
3.2.7 Построение эпюры нормальных и касательных напряжений по высоте сечения, в котором изгибающий момент достигает максимальной величины
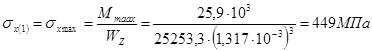
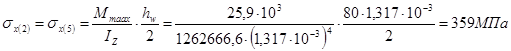
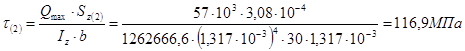
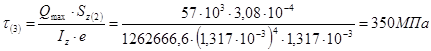
3.2.8 Определение главных, эквивалентных напряжений и построение эпюры эквивалентных напряжений по высоте сечения; определение опасной точки сечения
3.2.9 Проверка прочности балки
n
=
n > [ n ] условие прочности не выполняется
Список использованной литературы
1. Беляев Н.М. Сопротивление материалов. М: Наука, 1976
2. Копнов В.А. Сопротивление материалов. М: Высш. Шк., 2003
3. Писаренко Г.С. и др. Справочник по сопротивлению материалов. 1975
4. Феодосьев В.И. Сопротивление материалов. М: Наука, 1974
Похожие работы
-
Бревенчатый дом. Вековые традиции и современные технологии
Древесина – это ценный натуральный строительный материал, который позволяет максимально выразить индивидуальность жилища и создать атмосферу тепла и уюта.
-
Гидравлический привод протяжного станка
Курсовая работа по МЖГ «Гидравлический привод протяжного станка» Привод, гидравлическая схема которого представлена на рисунке, состоит из бака 1, который содержит масло (плотность ρ=850кг/м
-
Процедура расчета и создания стержней с заданными характеристиками
Курсовая работа Тема: Процедура расчета и создания стержней с заданными характеристиками Содержание 1 Основные аспекты создания стержней 1.1 Растяжение в центре и по бокам
-
Расчёт на прочность, стойкость и устойчивость элементов
Определение геометрических характеристик поперечного сечения бруса. Расчет на прочность и жесткость статических определимых балок при плоском изгибе, построение эпюры поперечных сил. Расчет статически не определимых систем, работающих на растяжение.
-
Проектирование главной схемы электрических соединений подстанции
Министерство образования Российской Федерации НГТУ Кафедра Э.С. Курсовая работа по дисциплине “Производство электрической энергии” Тема: Проектирование главной схемы электрических соединений подстанции.
-
Расчеты общей продольной прочности проектируемого контейнеровоза
Определение эйлеровых напряжений пластин судового корпуса. Изгибающие моменты и перерезывающие силы на тихой воде и при ударе волн в борта. Волновые изгибающие моменты перерезывающей силы. Расчет эквивалентного бруса в первом приближении сухогруза.
-
Расчет балки
Задача №1. привод крутящий момент балка Р = 13 кН, М = 9 кН·м, = 0,9 м, l = 1,1 м, α = 30°. Решение Составим расчетную схему балки, опоры заменим реакциями опор (рис. 1).
-
Конструирование узлов и деталей машин
Расчет веса частей бруса. Определение угла наклона сечения, для которого нормальное и касательное напряжения равны по абсолютной величине. Построение эпюров сечения, вычисление его диаметра. Определить передаточное отношение от входного колеса до водила.
-
Проектирование состава бетона
Курсовая работа по материаловедению студента Группа Санкт-Петербургский Государственный Политехнический Университет Инженерно-строительный факультет
-
Энергетический принцип расчета барьерных ограждений на мостах
Нештатные ситуации с транспортными средствами на дорогах нежелательное, но реальное явление. Барьерное ограждение предназначено для того, чтобы уменьшить материальные потери и даже жертвы.