Название: Определение абсолютной скорости и ускорения точки в механизме

Вид работы: контрольная работа

Рубрика: Промышленность и производство

Размер файла: 292.6 Kb

Скачать файл: referat.me-302248.docx

Краткое описание работы: Задача Для заданной механической системы определить ускорения грузов и натяжения в ветвях нитей, к которым прикреплены грузы. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.

Определение абсолютной скорости и ускорения точки в механизме

Задача 1

Для заданной механической системы определить ускорения грузов и натяжения в ветвях нитей, к которым прикреплены грузы. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.

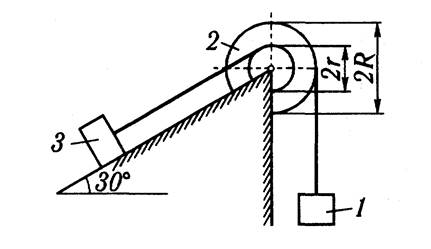
Данные:

1. G₁ =2G, сила тяжести

2. G₂ =G, сила тяжести

3. G₃ =2G, сила тяжести

4. R/r=3

5. i_{2 x} =2r, радиус инерции

6. f =0.2, коэффициент трения скольжения

Решение

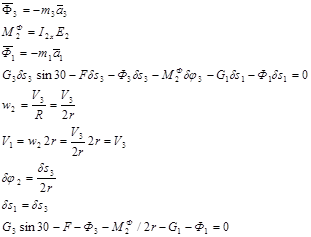
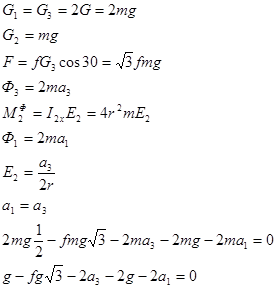
т.к. a₁ =a₃ тозаменим a₁ =a₃ =a

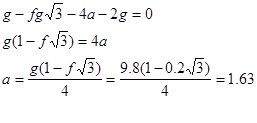
T_3-2

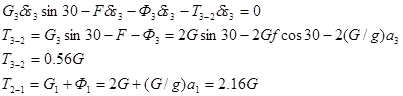
Задание K 2

Движение груза 1 должно описываться уравнением , где t-время (с), -некоторые постоянные. В начальный момент времени (t=0) положение груза определяется координатой , и он имеет скорость . Учесть, что в момент времени t=t₂ координата груза равна. Определить коэффициенты , при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t_1, скорость и ускорение груза и точки М одного из колес механизма.

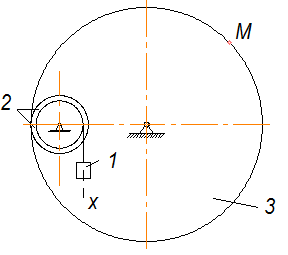
Данные:

7. R₂ =45,cм

8. r₂ =35, см

9. R₃ =105, см

10. x₀ =8, см

11. V₀ =5, см/с

12. x₂ =124, см

13. t₂ =4, см

14. t₁ =3, см

Решение

Нахождение коэффициентов

; ; ;

Скорость груза 1:

, ,

Уравнение движения груза 1:

Скорость груза 1:

;

Ускорение груза 1:

;

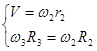
Результаты вычислений для заданного момента времени t=t₁

V, см/с	а, см/с2	, рад/с	Е3 , рад/с2	VM , см/с	, см/с2	, см/с2	, см/с2
41	12	0,48	0,14	50,4	24,2	14,7	28,3

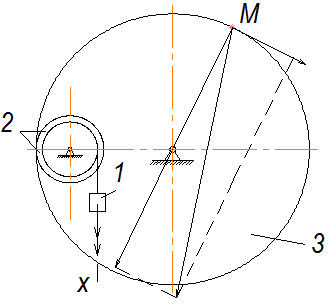
Вариант 6

Постановка задачи: Найти для заданного положения механизма скорости точек В и С, а также угловую скорость и угловое ускорение звена к которому эти точки принадлежат.

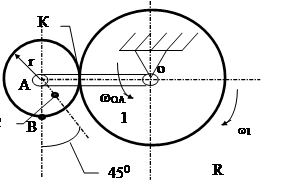
Дано: r = 15 cм, OA=40 см, AC=6 см, w_OA =1 рад/с, w₁ =1 рад/с, e_OA =0 рад/с² .

Найдем скорость точек С и В приняв за полюс точку А

Тогда скорости точек В и С запишутся как соответствующие суммы скоростей:

скорость полюса А во вращательном движении относительно точки о и скорость точки во вращательном движении относительно полюса А

U_c =U_e +U_r где Ue=w_OA *OA; Ur=w₂ *AC; U_r =1*40=40 cм/c

U_b =U_e +U_r где Ue=w_OA *OA; Ur=w₂ *AB

Найдем угловую скорость w₂

w₂ =U_A /AC_U

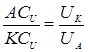где U_K = w₁ *OK ; ОК=ОА-rOK=40-15=25; U_K =1*25=25 cм/c;

КС_U =r-AC_U ; U_А = w_ОА *ОА =1*40=40; => 40AC_U =25*15-25AC_U =5.769 см

w₂ =40/5.769=6.933

получаем скорости точек С и В:

U_{C r} =6.933*6=41.59cм/c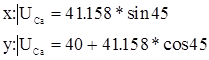

U_Ca =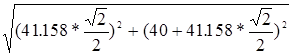=194.978см/с

U_Br =6.933*15=103.995 cм/c

U_Ba = cм/c

Найдем ускорения точек С и В

а_а =а_A +aⁿ +a^t

а_A =w_оа ² *OA=40см/с² ; ткe_OA =0 то a^t =0;

для точки С aⁿ =w₂ ² *AC=48.066*6=288.39 см/с² ;

а_{а C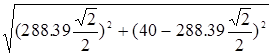} ==331.71

для точки Baⁿ =w₂ ² *AВ=48.066*15=720.099 см/с² ;

а_{а B} = см/с²

Вариант № 7

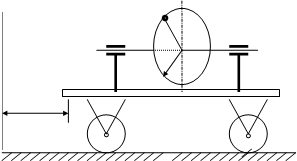
Точка М движется относительно тела D Определить абсолютную скорость и абсолютное ускорение точки М.

Дано: х_е =х_е (t)=3t+0.27t³ (см), t₁ =10/3 (см), R=15 (см), j_r =0.15pt³ .

Решение

Примем за центр отсчета точку О- центр вала К тогда скорость центра в движении вдоль оси Х определится как U_е = х_е `(t)=3+0.81t<sup>2</sup> , а угловая скорость точки М во вращательном движении вокруг центра О определится как w=j<sub>r</sub> `=0.45pt² . Тогда относительная скорость точки М определится как U_r =0.45pt² *R.

Абсолютная скорость точки в момент времени t=10/3 =>

U_a ====235.924 (см/c).

Найдем абсолютное ускорение точки М.

a_a = a_e +a_r +a_cor

Переносное ускорение точки М:

а_e = U_e `=1.62t.

Относительное ускорение

a_r =где а_t =U_r `=0.9pt*R, a_n =w² *R.

a_r =

Кореалисово ускорение a_cor =2w_е U_r =0. т.к. w_е =const.

Т. к. a_r перпендикулярно а_е то

a_a =a_r + а_е =

a_a (t=10/3)=381.37

Исходные данные приведены в таблице:

m1	m2	m3	R3 ,см	α	β	f	δ	S,м
m	3m	m	28	30º	45º	0,10	0,2	1,5	?

Применим к решению задачи теорему об изменении кинетической энергии механической системы:

, где , т.к. в начале

система покоилась.

- сумма работ внутренних сил (нерастяжимых нитей абсолютно твердых тел).

Следовательно, уравнение (1) принимает вид

Вычислим кинетическую энергию системы:

Тело 1 движется поступательно

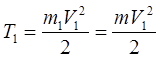
Тело 2 вращается вокруг оси Z

;

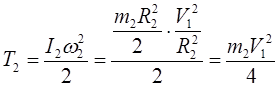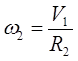
Тело 3 совершает плоскопараллельное движение, P-мгновенный центр скоростей

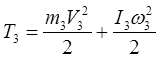; где ;

;

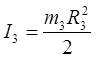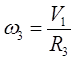
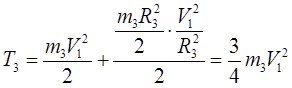
Подставим в уравнение:

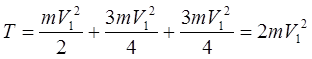
Найдем работу всех внешних сил при перемещении груза 1 на S₁

,

где ,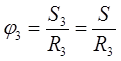

и , т.к. и

, т.к. центр масс неподвижен

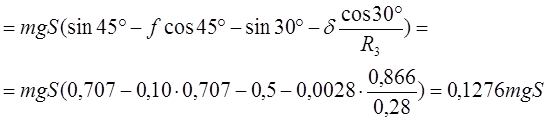
Подставим и во уравнение:

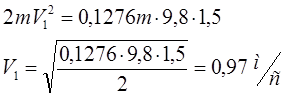
ОТВЕТ:

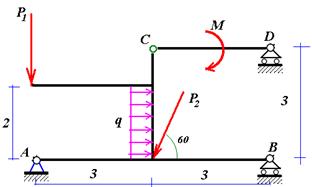
Рис. 1. Условие

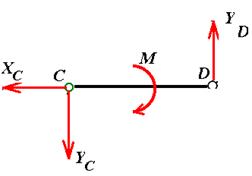
Рис. 2. Составим уравнения равновесия части CD

X_k = X_c = 0

Y_k = Y_c + Y_D = 0

M_c = 3Y_D  M = 0

Составим уравнения равновесия части ACB

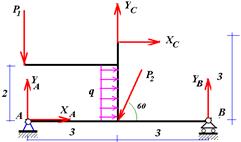
Рис. 3

X_k = X_A + X_c P₂ cos60 +2q=0

Y_k = Y_A + Y_B + Y_c  P₂ sin60 P₁ = 0

M_A = 2q·1 + 6Y_B 3P₂ sin60 +3Y_c 3X_c =0

Решаем систему уравнений и получаем (в кН) X_c =0, Y_c =6.66, X_a =0.5, Y_a =10.03, Y_b =0.364, Y_d =6.667.

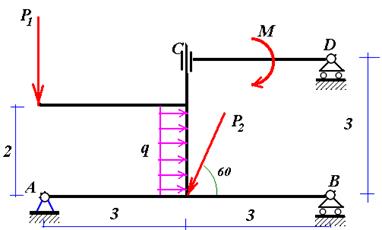
Рис. 4. Анализируя реакцию Y_B , заменим шарнир на скользящую заделку. Из уравнения проекций на ось y для части CD получим Y_d =0.

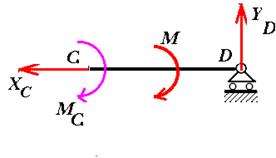
Рис. 5. Запишем сумму моментов для всей системы в целом относительно опоры A (Рис.

6)

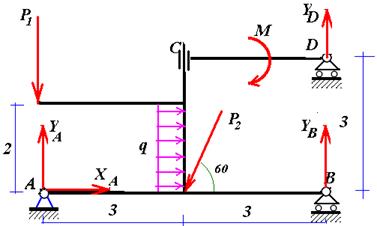
Рис. 6

M_A = 2q·1 + 6Y_B 3P₂ sin60  M=0

Вычислим Y_b =7.031кН.

Вывод: для первого способа соединения исследуемая реакция меньше.