Название: Классификация объектов нечисловой природы на основе непараметрических оценок плотности

Вид работы: доклад

Рубрика: Промышленность и производство

Размер файла: 73.03 Kb

Скачать файл: referat.me-304125.docx

Краткое описание работы: КЛАССИФИКАЦИЯ ОБЪЕКТОВ НЕЧИСЛОВОЙ ПРИРОДЫ НА ОСНОВЕ НЕПАРАМЕТРИЧЕСКИХ ОЦЕНОК ПЛОТНОСТИ. В СССР в середине 70-х годов активно ведутся работы по статистическому анализу нечисловых данных [1]. В настоящее время во Всесоюзном центре статистических методов и информатики мы при разработке методических документов и программных продуктов по прикладной статистике делим ее на четыре части соответственно виду обрабатываемых статистических данных: на статистику случайных величин, многомерный статистический анализ, статистику временных рядов и случайных процессов, статистику объектов нечисловой природы (другими словами, статистику нечисловых данных).

Классификация объектов нечисловой природы на основе непараметрических оценок плотности

КЛАССИФИКАЦИЯ ОБЪЕКТОВ НЕЧИСЛОВОЙ ПРИРОДЫ НА ОСНОВЕ НЕПАРАМЕТРИЧЕСКИХ ОЦЕНОК ПЛОТНОСТИ.

В СССР в середине 70-х годов активно ведутся работы по статистическому анализу нечисловых данных [1]. В настоящее время во Всесоюзном центре статистических методов и информатики мы при разработке методических документов и программных продуктов по прикладной статистике делим ее на четыре части соответственно виду обрабатываемых статистических данных: на статистику случайных величин, многомерный статистический анализ, статистику временных рядов и случайных процессов, статистику объектов нечисловой природы (другими словами, статистику нечисловых данных).

Вероятностный и статистический анализ нечисловых данных сопровождали теорию вероятностей и математическую статистику с самого начала их развития. Типичными примерами являются урновые схемы и изучение рождаемости. Испытание Бернулли- вероятностная модель простейшего объекта нечисловой природы. Наиболее массовым применением статистических методов является, видимо, выборочный контроль качества продукции по альтернативному признаку (т. е. по признаку "годен” - “не годен"), относящийся, очевидно, к статистике объектов нечисловой природы [2].

Развитие прикладных исследований привело к необходимости рассмотрения в качестве статистических данных различных объектов нечисловой природы. Этот термин применяем к объектам, которые нецелесообразно рассматривать как описанные числами. Другими словами, речь идет об элементах пространства, не являющихся линейными (векторными). Примеры: бинарные отношения (ранжировки, разбиения, толерантности и т. д.); множества; нечеткие множества; результаты измерений в шкалах, отличной от абсолютной; как обобщение перечисленных объектов - элементы пространств общей природы. Для результатов наблюдений, являющихся объектами нечисловой природы, рассматривают [1] классические задачи статистики: описание данных (включая классификацию) оценивание (параметров, характеристик, плотности распределения, регрессионной зависимости и т. д.).

Математический аппарат статистики объектов нечисловой природы основан не на свойстве линейности пространства, а на применении симметрик и метрик в нем, поэтому существенно отличается от классического.

В прикладных работах наиболее распространенный пример объектов нечисловой природы - разнотипные данные. В этом случае реальный объект описывается вектором, часть координат которого - значения количественных признаков, а часть - качественных (номинальных и порядковых).

Основная цель настоящего раздела - обосновать новый подход [3] к классификации в пространствах произвольной природы, основанный на построении не параметрических оценок плотности распределений вероятности в таких пространствах [4].

" Пусть - измеримое пространство,. и . суть -конечные меры на ., причем абсолютно непрерывна относительно , т. е. из равенства. . =0 следует равенство =0, где .. В этом случае на существует неотрицательная измеримая функция такая, что

для любого Функция называется производной Родона-Никодима меры по мере , а в случае, когда - вероятностная мера, также плотностью вероятности по отношению к . " [5]

Будем считать, что в пространстве объектов нечисловой природы фиксирована некоторая мера , а мера соответствует распределению Р случайного элемента со знаниями в измеримом пространстве , т. е.

Если - пространство из конечного числа точек, то в качестве меры можно использовать считающую меру (приписывающую единичный вес каждой точке), т. е. , или

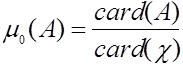
В случае считающей меры значение плотности в точке совпадает с вероятностью попасть в точку , т. е.

Многие методы классификации используют расстояния или меры близости между объектами или признаками. Такие методы пригодны и для классификации объектов нечисловой природы, лишь бы в соответствующем пространстве было определено расстояние или мера близости. Таким образом, широко известные иерархические агломеративные алгоритмы ближайшего соседа, дальнего соседа, средней связи и др., результатом работы которых являются дендрограммы, на самом деле относятся к статистике объектов нечисловой природы.

Не пытаясь рассмотреть все многообразие методов классификации в статистике объектов нечисловой природы (см., например, [6, 7]), сосредоточимся на тех из них, которые используют плотности распределения и их оценки. Зная плотности распределения классов, можно решать основные задачи классификации - как задачи выделения кластеров, так и задачи диагностики. В задачах кластер-анализа можно находить моды плотности и принимать их за центры кластеров или за начальные точки итерационных методов типа динамических сгущений. В задачах диагностики (дискриминации, распознавания образов с учителя) можно принимать решения о классификации объектов на основе отношения плотностей, соответствующих классам. При неизвестных плотностях представляется естественным использовать их состоятельные оценки. Корректность такой постановки, как правило, нетрудно обосновать, например, в стиле [8]. Таким образом, для переноса на пространства произвольной природы основных методов классификации рассматриваемого типа достаточно уметь оценивать плотность распределения вероятности в таких пространствах.

Методы оценивания плотности вероятности в пространствах общего вида предложен и первоначально изучены в [4]. В частности, в задачах классификации объектов нечисловой природы предлагаем использовать непараметрические ядерные оценки плотности типа Парзена-Розенблатта (этот вид оценок и его название введены нами в [4]):

,

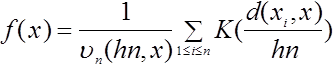где К: - ядерная функция - выборка по которой оценивается плотностью, - расстояние между элементом выборки и точкой , в которой оценивается плотность последовательность показателей размытости такова, что при 0 и n, а - нормирующий множитель, обеспечивающий выполнение условия

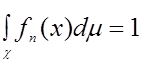
Оценки типа Парзена-Розенблатта - частный случай линейных оценок [4]. В теоретическом плане они выделяются тем, что удается получать результаты такого же типа, что в классическом одномерном случае (), но, разумеется, с помощью совсем иного математического аппарата.

Одна из основных идей состоит в том, чтобы согласовать между собой расстояние и меры . А именно, рассмотрим шары радиуса

и их меры

Предположим, что как функция при фиксированном непрерывна и строго возрастает. Введем функцию

Это - монотонное преобразование расстояния, а потому - метрика или симметрика (т. е. неравенство треугольника может быть не выполнено), которую, как и , можно рассматривать как меру близости между и .

Введем

.

Поскольку определена однозначно, то

^

где ., а потому

Переход от к напоминает классическое преобразование, использованное Н. В. Смирновым, , переводящее случайную величину с непрерывной функцией распределения в случайную величину , равномерно распределенную на [ 0, 1]. Оба рассматриваемых преобразования существенно упрощают дальнейшие рассмотрения.

Преобразование зависит от точки , что не влияет на дальнейшие рассуждения, поскольку ограничиваемся изучением сходимости в точке.

Функцию , для которой мера шара радиуса равна , называют [4] естественным показателем различия или естественной метрикой. В случае пространства и евклидовой метрики имеем

где -объем шара единичного радиуса в .

Поскольку можно записать, что

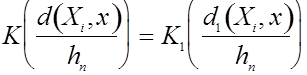
где

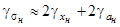
то переход от к соответствует переходу от к . Выгода от такого перехода заключается в том, что утверждения приобретают более простую формулировку.

ТЕОРЕМА 1. Пусть - естественная метрика,

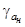
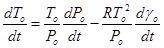
Плотность непрерывна в и ограничена на , причем . Тогда , оценка является состоятельной, т. е. по вероятности при ,

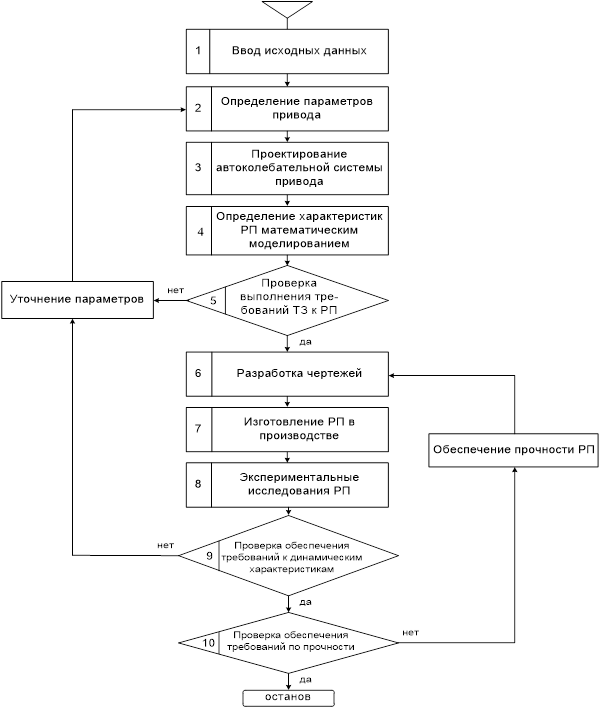
Теорема 1 доказана в [4]. Однако остается открытым вопрос о скорости сходимости ядерных оценок, т. е. о поведении величины

и об оптимальном выборе показателей размытости .

Введем круговое распределение и круговую плотность .

ТЕОРЕМА 2. Пусть ядерная функция непрерывна и при . Пусть круговая плотность допускает разложение

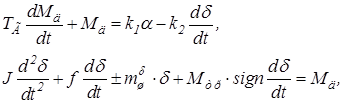
причем остаточный член равномерно ограничен [0, 1,...., ]. Пусть

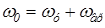
Тогда

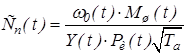
Величина достигает минимума, равного

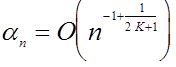
при

что совпадает с классическими результатами для (см. [9, с316]). Заметим, что для уменьшения смещения оценки приходится применять знакопеременные ядра .

В случае дискретных пространств естественных метрик не существует. Однако можно получить аналоги теорем 1 и 2 переходя к пределу не только по объему выборки , но и по параметру дискретности .

Пусть - последовательность конечных пространств, - расстояния в

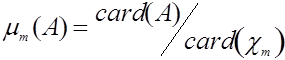для любого .

Положим

,

,

,

Тогда функции кусочно постоянны и имеют скачки в некоторых точках , причем .

ТЕОРЕМА 3. Если при (другими словами, при ), то существует последовательность параметров дискретности такая, что при , , справедливы заключения теорем 1 и 2.

ПРИМЕР 1. Пространство всех подмножеств конечного множества из элементов допускает [10, Пар 4. 3] аксиоматическое введение метрики 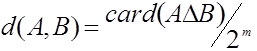, где - символ симметрической разности множеств. Рассмотрим непараметрическую оценку плотности типа Парзена - Розенблатта 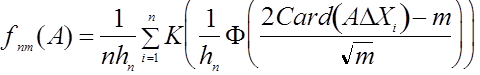, где - функция нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет условиям теоремы 3 .

ПРИМЕР 2. Рассмотрим пространство функций , определенных на конечном множестве 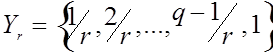со значениями в конечном множестве 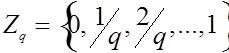. Это пространство можно интерпретировать как пространство нечетких множеств [11]. Очевидно, . Будем использовать расстояние . Непараметрическая оценка плотности имеет вид: .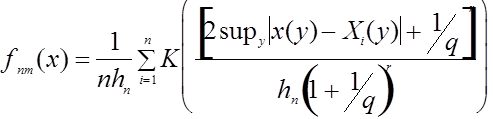

Если , , то при выполнены условия теоремы 3, а потому справедливы теоремы 1 и 2.

. ПРИМЕР 3. Рассматривая пространства ранжировок объект непреов, в качестве расстояния между ранжировками и . Тогда . не стремиться к 0 при ., условия теоремы 3 не выполнены.

Пространства разнотипных признаков - это декартово произведение непрерывных и дискретных пространств. Для него возможны различные постановки. Пусть, например, число градаций качественных признаков остается постоянным. Тогда непараметрическая оценка плотности сводится к произведению частоты попадания в точку в пространстве качественных признаков на классическую оценку Парзена-Розенблатта в пространстве количественных переменных. В общем случае расстояние можно, например, рассматривать как сумму евклидова расстояния между количественными факторами, расстояния между номинальными признаками (, если и , если ) и расстояния между порядковыми переменными (если и - номера градаций., то .

Наличие количественных факторов приводит к непрерывности и строгому возрастанию , а потому для непараметрических оценок плотности в пространствах разнотипных признаков справедливы теоремы 1 - 3.

Литература

1.Орлов А.И. Устойчивость в социально-экономических моделях.-М.Наука,1979.-296 с.

2.Орлов А.И. Экспертные оценки / Вопросы кибернетики. Вып.58.-М.: Научный Совет СССР по комплексной проблеме "Кибернетика", 1979.С.17-33.

3.Орлов А.И. / Тезисы докладов Четвертой международной Вильнюсской конференции по теории вероятностей и математической статистике: Том 2.-Вильнюс, Вильнюсский госуниверситет, 1985.С.278-280.

4.Орлов А.И. / Анализ нечисловой информации в социологических исследованиях.-М.Наука, 1985.С.58-92.

5.Орлов А.И. / Статистика. Вероятность. Экономика.-М.Наука,1985. С.99-107.

6.Орлов А.И. / Заводская лаборатория. 1987.Т.58. N3.С.90-91.

7.Орлов А.И. /Надежность и контроль качества. 1987.N6.С.54-59.

8.Рекомендации. Прикладная статистика. Методы обработки данных. Основные требования и характеристики.- М.:ВНИИС,1987.-64 с.

9.Кривцов В.С., Фомин В.Н., Орлов А.И. / Стандарты и качество. 1988.N3.С.32-36.

11.Колмогоров А.Н. Статистический приемочный контроль при допустимом числе дефектных изделий, равном нулю. - Л.: ДНТП, 1951. - 22 с.

12. Гнеденко Б.В. Математика и контроль качества продукции.- М.: Знание, 1978. - 64 с.

13. Беляев Ю.К. Вероятностные методы выборочного контроля.-М.: Наука, 1975. - 408 с.

14. Лумельский Я.П. Статистические оценки результатов контроля качества. - М.: Из-во стандартов, 1979. - 200 с.

15. Орлов А.И. Современные проблемы кибернетики: Прикладная статистика. - М.: Знание, 1981. с 3-14.

16. Статистические методы анализа экспертных оценок / Ученые записки по статистике, т. 29, -М.: Наука, 1977-384 с. 17.

17.Экспертные оценки в системных исследованиях / Сборник трудов. - Вып. 4. - М.: ВНИИСИ, 1970 - 120 с.

18. Экспертные оценки / Вопросы кибернетики. - Вып. 58. - М.: Научный Совет АН СССР по комплексной проблеме / "Кибернетика". 1979. - 200 с.