Название: Анализ качества САУ при случайных воздействиях и их оптимизация

Вид работы: реферат

Рубрика: Промышленность и производство

Размер файла: 42.92 Kb

Скачать файл: referat.me-299733.docx

Краткое описание работы: Оценка качества систем при детерминированных воздействиях, расчет ошибок с САУ при случайных воздействиях. Определение суммарной спектральной плотности ошибки, средней квадратичной ошибки. Статистическая оптимизация автоматических систем управления.

Анализ качества САУ при случайных воздействиях и их оптимизация

Предмет:

«Теория автоматического управления статических систем»

Тема:

«Анализ качества САУ при случайных воздействиях и их оптимизация»

Анализ качества САУ при случайных воздействиях

Так как устойчивость линейных систем является свойством системы и не зависит от характера воздействия, то устойчивость при случайных воздействиях определяется также, как и для детерминированных.

Качество систем при детерминированных воздействиях оценивается с помощью показателей качества, таких как tp, s, T и т.д. При случайных воздействиях они теряют смысл, так как входные и выходные величины являются случайными функциями времени и при исследовании рассматривают не сами процессы, а их статистические свойства, т.е. определяют не мгновенные значения процессов, а их средние значения.

При случайных воздействиях ошибка системы e(t) = x(t)-y(t) также является случайной величиной, при этом используют ее усредненное значение – среднюю квадратичную ошибку

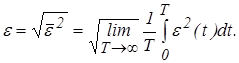(1)

Эта ошибка используется для оценки точности или качества систем при случайных воздействиях.

Недостатки средней квадратичной ошибки:

1.Она обеспечивает минимум не мгновенного, а среднего значения, при этом мгновенное значение может быть недопустимо большим.

2. Она недооценивает малые ошибки и придает чрезмерное значение большим ошибкам, так как ее значение возводится в квадрат.

Расчет ошибок с САУ при случайных воздействиях

Рассмотрим порядок расчета ошибок в системах управления при случайных воздействиях. Пусть задана система, приведенная на рис.1.

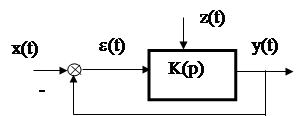Рис.1

Необходимо определить величину средней квадратичной ошибки -e если заданы Sxx(w) и Szz(w).

Рассмотрим несколько случаев.

Пусть действует только полезный сигнал x(t) а помеха z(t) отсутствует.

Спектральная плотность ошибки определяется соотношением:

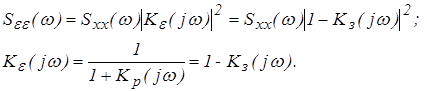(2)

Величина средней квадратичной ошибки -e определяется по формуле:

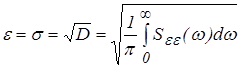. (3)

Значения интеграла от спектральной плотности табулированы и могут быть вычислены через коэффициенты полиномов выражения для спектральной плотности.

Пусть действует только помеха z(t) а полезный сигнал x(t) отсутствует.

Действие помехи рассматривается на выходе системы.

Спектральная плотность ошибки при этом определяется соотношением:

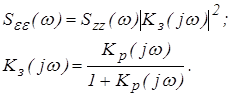(4)

3. Пусть действует и полезный сигнал x(t) и помеха z(t) и они не коррелированны.

Суммарная спектральная плотность ошибки при этом определяется соотношением:

(5)

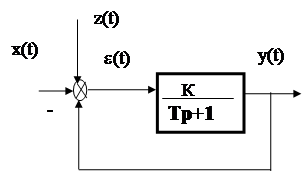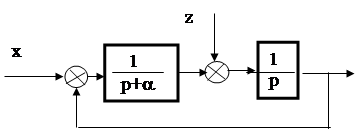
Пример 1. Для приведенной ниже системы (рис.2), определить величину средней квадратичной ошибки -e, если заданы Sxx(w) = c2 и Szz(w) = 0.

Рис. 2

Если сигнал и помеха некоррелированны, то суммарная спектральная плотность ошибки при этом определяется соотношением:

.

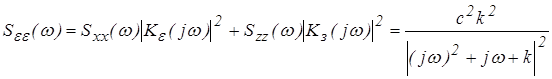Значения интеграла от спектральной плотности вычислим через коэффициенты полиномов выражения для спектральной плотности.

Величина средней квадратичной ошибки -e определяется по формуле:

.

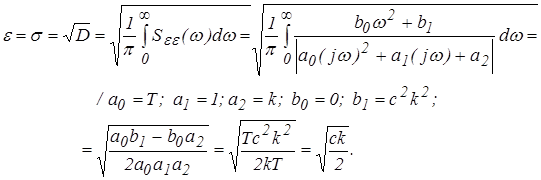Пример 2. Для системы приведенной на рис.3 определить спектральную плотность ошибки, вызванную действием помехи -z(t) со спектральной плотностью

y

Рис. 3

Решение: Спектральная плотность ошибки определяется из соотношений:

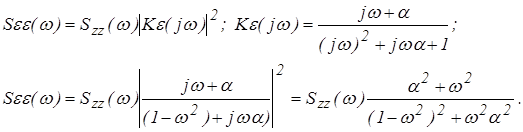
Статистическая оптимизация систем управления

При статистических исследованиях систем решаются задачи оптимизации, т.е. определение систем наилучших в определенном смысле (по точности, быстродействию, надежности и т.д.).

Оптимальной системой называют систему, обеспечивающую экстремум некоторого функционала, называемого критерием оптимальности.

При статистической оптимизации систем решаются следующие задачи:

Задача анализа.

Задача синтеза.

Задача анализа

Формулировка задачи

Дано: система с заданной структурой; статистические характеристики полезного сигнала x(t) и помехи z(t).

Определить: параметры системы, обеспечивающие минимальную величину средней квадратичной ошибки.

Рис.4

Схему исследуемой системы можно представить в виде, показанном на рис.1. При этом Ки(р) – передаточная функция идеальной системы, которая определяет закон преобразования полезного сигнала.

В системах, находящихся под действием случайного (или регулярного) входного сигнала и помехи возникает задача отделения сигнала от помехи и подавления (фильтрации) помехи. Кроме фильтрации в зависимости от оператора Ки(р) задача фильтрации сочетается с задачами:

1. Ки(р) = const – это задача воспроизведения, т.е. отделения полезного сигнала от помехи. Эта задача чаще всего используется для следящих систем.

2. Ки(р) = L(p) –задача преобразования и фильтрации. При этом L(p)- оператор преобразования.

Алгоритм решения задачи

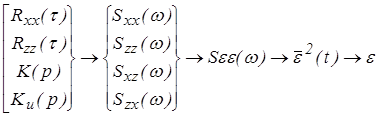. (6)

Величина средней квадратичной ошибки определяется по формуле:

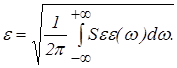(7)

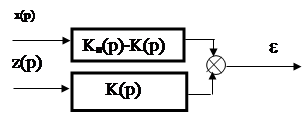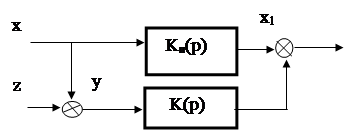
Схему исследуемой системы можно представить в виде, показанном на рис.2.

Рис. 5

Изображение ошибки равно:

(7)

Спектральная плотность ошибки равна:

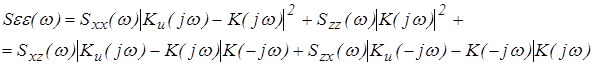Если сигналы не коррелированны то

Для определения дисперсии выходного сигнала необходимо вычислить интеграл вида

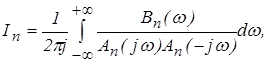(8)

где

Табулированные значения этих интегралов, вычисленные через коэффициенты полиномов A(jw) и B(w), приведены в литературе по системам управления.

В таблице 1 приведены табулированные значения интегралов для n £ 3.

Таблица 1

De 3 2 1

b0 2a0 a1

a0 b1 –b0 a2 2a0 a1 a2

a0 a3 b1 – a2 a3 b0 –a0 a1 b2 2a0 a3 (a0 a3 –a1 a2 )

Используя таблицу, получим зависимость

. (9)

Оптимальные значения параметров получим с помощью частных производных.

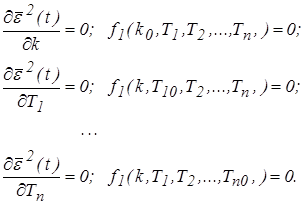(10)

Решив систему уравнений, получим оптимальные значения параметров k0, T10, …, Tn0.

Если путем изменения варьируемых параметров системы не удается добиться требуемого качества, то необходимо решать задачу синтеза, т.е. менять структуру системы.

Литература

1. Егупов Н.Д., Пупков К.А., Баркин А.И. Методы классической и современной теории автоматического управления: В 5 тт: Т. 4: Теория оптимизации систем автоматического управления Изд-во: МГТУ им. Н.Э. Баумана, 2004.

2. Зотов М.Г. Многокритериальное конструирование систем автоматического управления Издательство: БИНОМ. Лаборатория знаний, 2004. – 375с.

3. Меркин Д.Р. Введение в теорию устойчивости движения, 198

4. Светлицкий В.А., Стасенко И.В. Сборник задач по теории колебаний, 1973

5. Теория автоматического управления. Учеб. для вузов по спец. "Автоматика и телемеханика". В 2-х ч./ Н.А. Бабаков, А.А. Воронов и др.: Под ред. А.А. Воронова. - 2-е изд., перераб. и доп. - М.: Высш. шк., 198 - 367с., ил.