Название: Расчет параметров идеального газового потока в камере ракетного двигателя
Вид работы: курсовая работа
Рубрика: Промышленность и производство
Размер файла: 685.46 Kb
Скачать файл: referat.me-304710.docx
Краткое описание работы: Агентство по образованию Российской Федерации Самарский Государственный Аэрокосмический Университет имени академика С.П. Королева (Национальный исследовательский университет)
Расчет параметров идеального газового потока в камере ракетного двигателя
°УХЭвбвТЮ ЯЮ ЮСаРЧЮТРЭШо АЮббШЩбЪЮЩ ДХФХаРжШШ БРЬРабЪШЩ іЮбгФРабвТХЭЭлЩ °наЮЪЮбЬШзХбЪШЩ ГЭШТХабШвХв ШЬХЭШ РЪРФХЬШЪР Б.ї. єЮаЮЫХТР
(ЅРжШЮЭРЫмЭлЩ ШббЫХФЮТРвХЫмбЪШЩ гЭШТХабШвХв)
єРдХФаР вХЯЫЮвХеЭШЪШ Ш вХЯЫЮТле ФТШУРвХЫХЩ
АРбзХвЭЮ-ЯЮпбЭШвХЫмЭРп ЧРЯШбЪР Ъ ЪгабЮТЮЩ аРСЮвХ:
«А°БЗµВ ї°А°јµВАѕІ ёґµ°»МЅѕіѕ і°·ѕІѕіѕ їѕВѕє° І є°јµАµ А°єµВЅѕіѕ ґІёі°Вµ»П»
ЯЮ ФШбжШЯЫШЭХ «јХеРЭШЪР ЦШФЪЮбвХЩ Ш УРЧЮТ»
ІРаШРЭв р13
ІлЯЮЫЭШЫ:
бвгФХЭв Уа. 2301
єЫШЯШЪЮТ Ѕ.О.
їаЮТХаШЫ:
Ъ.в.Э. ґШФХЭЪЮ °. °.
БРЬРаР 2010
АµДµА°В
єгабЮТРп аРСЮвР.
їЮпбЭШвХЫмЭРп ЧРЯШбЪР: 50 бва., 5 аШб., 4 вРСЫШж, 3 ЯаШЫЮЦХЭШп, 3 ШбвЮзЭШЪР.
іаРдШзХбЪРп ФЮЪгЬХЭвРжШп: 1 ЫШбв дЮаЬРвР A3.
є°Ѕ°» їµАµјµЅЅѕіѕ БµЗµЅёП, їАѕДё»М БІµАЕ·ІГєѕІѕіѕ Бѕї»°, єАёВёЗµБєѕµ БµЗµЅёµ, Бѕї»ѕ »°І°»П, ґ°І»µЅёµ, ВµјїµА°ВГА°, БєѕАѕБВМ, А°БЕѕґ, їАПјѕ№ Бє°Зѕє Гї»ѕВЅµЅёП, БВАГП і°·°, А°ґёГБ БµЗµЅёП Бѕї»°, і°·ѕІЛ№ їѕВѕє, ґѕ·ІГєѕІѕµ ВµЗµЅёµ і°·°, ёґµ°»МЅЛ№ і°·.
І ФРЭЭЮЩ ЪгабЮТЮЩ аРСЮвХ ТлЯЮЫЭХЭл аРбзХвл УХЮЬХваШзХбЪШе ЯРаРЬХваЮТ ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп, ЯРаРЬХваЮТ ШФХРЫмЭЮУЮ УРЧЮТЮУЮ ЯЮвЮЪР Т ЪРЬХаХ аРЪХвЭЮУЮ ФТШУРвХЫп, беХЬР ЪЮвЮаЮУЮ ЯаХФбвРТЫХЭР Т ЯаШЫЮЦХЭШШ, ЯЮбваЮХЭл УаРдШЪШ ШЧЬХЭХЭШп ЮбЭЮТЭле ТХЫШзШЭ.
іРЧЮТлЩ ЯЮвЮЪ ЯЮбвгЯРХв Т бТХаеЧТгЪЮТЮХ бЮЯЫЮ б ЭРзРЫмЭлЬ бХзХЭШХЬ 0
, гЧЪШЬ бХзХЭШХЬ г
, ТлеЮФЭлЬ бХзХЭШХЬ a
, ЯЫЮйРФШ ЪЮвЮале аРТЭл бЮЮвТХвбвТХЭЭЮ S0
, Sг
, Sa
. ёЧ бЮЯЫР УРЧ ТлвХЪРХв ТЮ ТЭХиЭоо баХФг, ФРТЫХЭШХ Т ЪЮвЮаЮЩ аРТЭЮ ![]() (ШбеЮФЭРп ЯЮбвРЭЮТЪР ЧРФРзШ) .
(ШбеЮФЭРп ЯЮбвРЭЮТЪР ЧРФРзШ) .
· °ґ°Ѕёµ
·РФРЭл бЫХФгойШХ ТХЫШзШЭл ЯРаРЬХваЮТ:
![]() - ЮвЭЮиХЭШХ вХЯЫЮХЬЪЮбвШ УРЧР ЯаШ ЯЮбвЮпЭЭЮЬ ФРТЫХЭШШ Ъ ХУЮ вХЯЫЮХЬЪЮбвШ ЯаШ ЯЮбвЮпЭЭЮЬ ЮСкХЬХ .
- ЮвЭЮиХЭШХ вХЯЫЮХЬЪЮбвШ УРЧР ЯаШ ЯЮбвЮпЭЭЮЬ ФРТЫХЭШШ Ъ ХУЮ вХЯЫЮХЬЪЮбвШ ЯаШ ЯЮбвЮпЭЭЮЬ ЮСкХЬХ .
![]() - гФХЫмЭРп УРЧЮТРп ЯЮбвЮпЭЭРп .
- гФХЫмЭРп УРЧЮТРп ЯЮбвЮпЭЭРп .
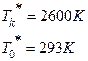 - вХЬЯХаРвгал вЮаЬЮЦХЭШп УРЧЮТЮУЮ ЯЮвЮЪР ЯаШ ТвХЪРЭШШ ХХ Т ЪРЬХаг бУЮаРЭШп Ш Т ЪЮЭжХ ХХ (ЯХаХФ бЮЯЫЮЬ) .
- вХЬЯХаРвгал вЮаЬЮЦХЭШп УРЧЮТЮУЮ ЯЮвЮЪР ЯаШ ТвХЪРЭШШ ХХ Т ЪРЬХаг бУЮаРЭШп Ш Т ЪЮЭжХ ХХ (ЯХаХФ бЮЯЫЮЬ) .
![]() - ФРТЫХЭШХ Т УРЧЮТЮЬ ЯЮвЮЪХ Т бХзХЭШШ 0 .
- ФРТЫХЭШХ Т УРЧЮТЮЬ ЯЮвЮЪХ Т бХзХЭШШ 0 .
![]() - ЮвЭЮиХЭШХ ЯЫЮйРФХЩ
- ЮвЭЮиХЭШХ ЯЫЮйРФХЩ ![]() .
.
![]() - аРФШгб гЧЪЮУЮ бХзХЭШп бЮЯЫР .
- аРФШгб гЧЪЮУЮ бХзХЭШп бЮЯЫР .
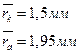 - ЮвЭЮиХЭШХ аРФШгбЮТ ЪРЬХал бУЮаРЭШп
- ЮвЭЮиХЭШХ аРФШгбЮТ ЪРЬХал бУЮаРЭШп ![]() Ш ТлеЮФЭЮУЮ бХзХЭШп бЮЯЫР
Ш ТлеЮФЭЮУЮ бХзХЭШп бЮЯЫР ![]() Ъ аРФШгбг
Ъ аРФШгбг ![]() .
.
![]() - ЮвЭЮиХЭШХ ФЫШЭл бТХаеЧТгЪЮТЮЩ зРбвШ бЮЯЫР
- ЮвЭЮиХЭШХ ФЫШЭл бТХаеЧТгЪЮТЮЩ зРбвШ бЮЯЫР ![]() Ъ аРФШгбг
Ъ аРФШгбг ![]() .
.
 - гУЫл ЬХЦФг ЪРбРвХЫмЭлЬШ Ъ ЯаЮдШЫо бЮЯЫР Т гЧЪЮЬ Ш ТлеЮФЭЮЬ бХзХЭШпе Ш Юбмо бЮЯЫР .
- гУЫл ЬХЦФг ЪРбРвХЫмЭлЬШ Ъ ЯаЮдШЫо бЮЯЫР Т гЧЪЮЬ Ш ТлеЮФЭЮЬ бХзХЭШпе Ш Юбмо бЮЯЫР .
ґЮЯгйХЭШп
іРЧ ШФХРЫмЭлЩ, ЭХТпЧЪШЩ. ВХзХЭШХ УРЧР Т бЮЯЫХ бЯЫЮиЭЮХ, бвРжШЮЭРаЭЮХ, нЭХаУЮШЧЮЫШаЮТРЭЭЮХ. АРбеЮФ Т ЪРЦФЮЬ бХзХЭШШ ЮФШЭРЪЮТлЩ. І бХзХЭШШ 0 – ФЮЧТгЪЮТЮЩ УРЧЮТлЩ ЯЮвЮЪ. БЪРзЮЪ гЯЫЮвЭХЭШп Т УРЧЮТЮЬ ЯЮвЮЪХ ЯапЬЮЩ Ш нЭХаУЮШЧЮЫШаЮТРЭЭлЩ. ёЧ ЪРЭРЫР УРЧЮТлЩ ЯЮвЮЪ ТлвХЪРХв Т ЮЪагЦРойго баХФг б ФРТЫХЭШХЬ аРТЭлЬ ФРТЫХЭШо ЭРагЦЭЮЬг (pa =pЭ ). ¶ШТлХ бХзХЭШп бзШвРвм ЯЫЮбЪШЬШ бХзХЭШпЬШ, ЭЮаЬРЫмЭлЬШ ЮбШ ЯЮвЮЪР (ЮбШ бЮЯЫР).
АРббзШвлТРХЬлХ аХЦШЬл УРЧЮТЮУЮ ЯЮвЮЪР
І ЪгабЮТЮЩ аРСЮвХ аРббзШвлТРовбп бЫХФгойШХ аХЦШЬл ШФХРЫмЭЮУЮ ЯЮвЮЪР Т бТХаеЧТгЪЮТЮЬ бЮЯЫХ:
1) АРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг (бЮЯЫг »РТРЫп).
2) ЅХаРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т ТлеЮФЭЮЬ бХзХЭШШ a.
3) ЅХаРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ 5.
4) ЅХаРбзХвЭлЩ аХЦШЬ вХзХЭШп УРЧР, бЮЮвТХвбвТгойШЩ бТХаеЧТгЪЮТЮЬг бЮЯЫг бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ 4.
5) ґЮЧТгЪЮТЮХ вХзХЭШХ УРЧР ЯЮ ТбХЬг ЪРЭРЫг, ЭЮ ЯаШ ЪаШвШзХбЪЮЬ бЮбвЮпЭШШ УРЧЮТЮУЮ ЯЮвЮЪР Т гЧЪЮЬ бХзХЭШШ (λг = 1).
БЮФХаЦРЭШХ
АµДµА°В........................................................................................................................................................................... 2
·°ґ°Ѕёµ........................................................................................................................................................................... 3
ёБїѕ»М·ѕІ°ЅЅЛµ БёјІѕ»Л......................................................................................................................... 6
1. їЮбваЮХЭШХ ЯаЮдШЫп ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп....................................................... 7
2. АРбзсв ЯХаТЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР............................................................................. 8
3. АРбзсв ТвЮаЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР........................................................................... 22
4. АРбзсв ваХвмХУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР........................................................................ 24
5. АРбзсв зХвТсавЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.................................................................. 27
6. АРбзсв ЯпвЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР............................................................................. 32
7. АРбзсв ШЬЯгЫмбЮТ УРЧЮТЮУЮ ЯЮвЮЪР............................................................................................ 36
8. АРбзсв бШЫ Ш впУШ........................................................................................................................................... 38
·РЪЫозХЭШХ............................................................................................................................................................. 40
БЯШбЮЪ ШбЯЮЫмЧгХЬле ШбвЮзЭШЪЮТ................................................................................................. 41
їАё»ѕ¶µЅёµ Р........................................................................................................................................................ 42
їАё»ѕ¶µЅёµ ±........................................................................................................................................................ 43
їАё»ѕ¶µЅёµ І........................................................................................................................................................ 46
ёБїѕ»М·ѕІ°ЅЅЛµ БёјІѕ»Л
r –аРФШгб, ЬЬ
S –ЯЫЮйРФм, ЬЬ2
q –УРЧЮФШЭРЬШзХбЪРп дгЭЪжШп аРбеЮФР ШЫШ ЯаШТХФХЭЭлЩ аРбеЮФ
λ –ЯаШТХФХЭЭРп бЪЮаЮбвм
M –зШбЫЮ јРеР
τ –іґД вХЬЯХаРвгал
π –іґД ФРТЫХЭШп
e –іґД ЯЫЮвЭЮбвШ
T* – вХЬЯХаРвгаР вЮаЬЮЦХЭШп, є
T – бвРвШзХбЪРп вХЬЯХаРвгаР, є
p* – ФРТЫХЭШХ вЮаЬЮЦХЭШп, їР
p – бвРвШзХбЪЮХ ФРТЫХЭШХ, їР
ρ* – ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп, ЪУ/Ь3
ρ – бвРвШзХбЪРп ЯЫЮвЭЮбвм, ЪУ/Ь3
aЪа – ЪаШвШзХбЪРп бЪЮаЮбвм ЧТгЪР, Ь/б
a – ЬХбвЭРп бЪЮаЮбвм ЧТгЪР, Ь/б
c – бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР, Ь/б
G – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР, ЪУ/б
ƒ – іґД ШЬЯгЫмбР
pЭ – ФРТЫХЭШХ ТЮ ТЭХиЭХЩ баХФХ, їР
Д – ШЬЯгЫмб УРЧЮТЮУЮ ЯЮвЮЪР, Ѕ
σЯ – ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп Т ЯапЬЮЬ бЪРзЪХ гЯЫЮвЭХЭШп
σТ.а. – ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп ЯаШ ТЭХЧРЯЭЮЬ аРбиШаХЭШШ
σВ – ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп ЯаШ ЯЮФТЮФХ вХЯЫЮвл
P0-г – бШЫР ТЮЧФХЩбвТШп УРЧЮТЮУЮ ЯЮвЮЪР ЭР ФЮЧТгЪЮТго зРбвм бЮЯЫР, Ѕ
Pг- a – бШЫР ТЮЧФХЩбвТШп УРЧЮТЮУЮ ЯЮвЮЪР ЭР бТХаеЧТгЪЮТго зРбвм бЮЯЫР, Ѕ
P0- a – бШЫР ТЮЧФХЩбвТШп УРЧЮТЮУЮ ЯЮвЮЪР ЭР бЮЯЫЮ Т жХЫЮЬ, Ѕ
PТЭгв. – ТЭгваХЭЭпп бЮбвРТЫпойРп ЯЮЫЭЮЩ впУШ, Ѕ
PЭРа. – ЭРагЦЭРп бЮбвРТЫпойРп ЯЮЫЭЮЩ впУШ, Ѕ
P – ЯЮЫЭРп впУР ФТШУРвХЫп, Ѕ
1. їЮбваЮХЭШХ ЯаЮдШЫп ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп.
АРббзШвРХЬ ЧЭРзХЭШп ЯРаРЬХваЮТ аРЪХвЭЮУЮ ФТШУРвХЫп б ЯЮЬЮймо ШбеЮФЭле ФРЭЭле:
1) ФЫШЭР ЪРЬХал бУЮаРЭШп:
![]() ,
,
2) ФЫШЭР ФЮЧТгЪЮТЮЩ зРбвШ бЮЯЫР:
![]() ,
,
3) ФЫШЭР бТХаеЧТгЪЮТЮЩ зРбвШ бЮЯЫР:
![]() ,
,
4) аРФШгб ЪРЬХал бУЮаРЭШп:
![]() ,
,
5) аРФШгб УРЧЮТЮУЮ ЯЮвЮЪР ЯаШ ТеЮФХ Т ЪРЬХаг бУЮаРЭШп:
![]() ,
,
6) аРФШгб ТлеЮФЭЮУЮ бХзХЭШп бЮЯЫР:
![]() ,
,
7) еРаРЪвХаЭлХ аРббвЮпЭШп бХзХЭШЩ 1, 2, 3, 4, 5 бЮЮвТХвбвТХЭЭЮ:
x1 =0.35∙ xЪ =0.35∙134=46,9 ЬЬ;
x2 =0.5∙ xг =0.5∙123,0869=61,5435 ЬЬ;
x3 =0.2∙ xг =0.2∙123,0869=24,6174 ЬЬ;
x4 =0.2∙ xa =0.2∙241,87=48,3740 ЬЬ;
x5 =0.6∙ xa =0.6∙241,87=145,122 ЬЬ.
їЮ аРббзШвРЭЭлЬ ЯРаРЬХваРЬ ЯЮбваЮШЬ ЯаЮдШЫм ЪРЬХал бУЮаРЭШп бЬ. ЯаШЫЮЦХЭШХ. їЮ ЯаЮдШЫо ЪРЬХал ЮЯаХФХЫпХЬ аРФШгбл ЯаЮЬХЦгвЮзЭле аРбзсвЭле бХзХЭШЩ r2 , r3 , r4 , r5 :
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
АРббзШвлТРХЬ ЯЫЮйРФШ ТбХе бХзХЭШЩ ЯЮ дЮаЬгЫХ:
![]()
УФХ ![]() – аРФШгб еРаРЪвХаЭЮУЮ бХзХЭШп, ЬЬ:
– аРФШгб еРаРЪвХаЭЮУЮ бХзХЭШп, ЬЬ:
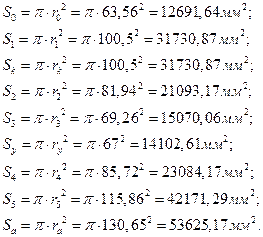
2. АРбзсв ЯХаТЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.
![]() (
(![]() ).
).
АРббзШвРХЬ ЯРаРЬХвал ЯЮвЮЪР ЯаШ бТХаеЧТгЪЮТЮЬ ШбвХзХЭШШ УРЧР ШЧ бЮЯЫР.
1) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «Ъ»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]()
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() k
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
k
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
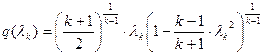 ,
,
ЯЮЫгзРХЬ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
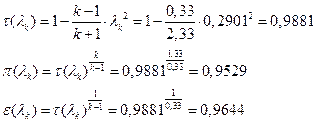
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
ЅРЩФсЬ зШбЫЮ јРеР:
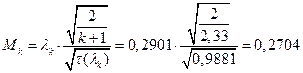
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
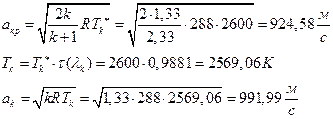
УФХ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
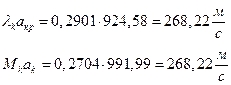
2) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «0»:
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() 0
ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЪЮЫШзХбвТР ФТШЦХЭШп ФЫп УРЧР (бЬ. ЯаШЫЮЦХЭШХ 3), ЭРеЮФпйХУЮбп Т ЪРЬХаХ бУЮаРЭШп ЬХЦФг бХзХЭШпЬШ «0» Ш «k»), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
0
ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЪЮЫШзХбвТР ФТШЦХЭШп ФЫп УРЧР (бЬ. ЯаШЫЮЦХЭШХ 3), ЭРеЮФпйХУЮбп Т ЪРЬХаХ бУЮаРЭШп ЬХЦФг бХзХЭШпЬШ «0» Ш «k»), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
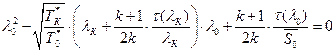 ,
,
ЯЮЫгзРХЬ ![]() .
.
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
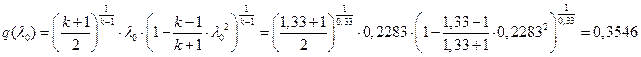
![]()
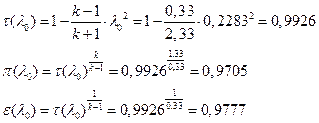
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ аРбеЮФР, вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ аРбеЮФР, вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
ЅРЩФсЬ зШбЫЮ јРеР:

ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
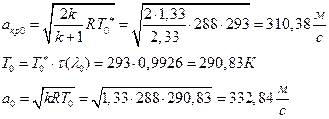
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
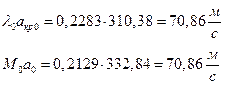
ЅРЩФсЬ ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп:
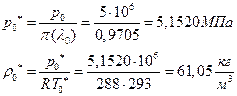
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
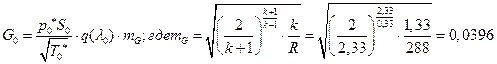
![]()
![]()
УФХ ![]() 0– бвРвШзХбЪРп ЯЫЮвЭЮбвм,
0– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
3) ІлзШбЫШЬ ЮбвРТиШХбп ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР Т бХзХЭШШ «k»:
ЅРЩФХЬ ЧЭРзХЭШХ ФРТЫХЭШп ШЧ ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЭХаРЧалТЭЮбвШ ФЫп ЦШТле бХзХЭШЩ «0» Ш «k» УРЧЮТЮУЮ ЯЮвЮЪР: ![]() ;
;
![]()
ЅРЩФсЬ ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп:
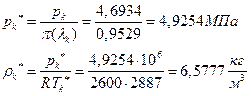
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
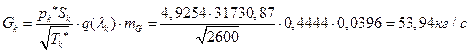
![]()
УФХ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
4) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «1»:
ЅРЩФХЬ λ1 зХаХЧ ФШбЪаШЬШЭРЭв
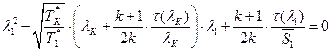 , УФХ
, УФХ ![]() ;
;
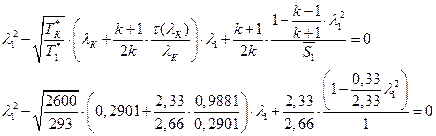
їЮЫгзРХЬ![]() .
.
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
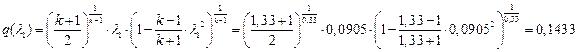
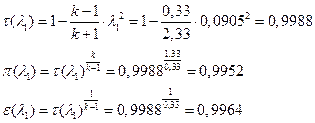
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ аРбеЮФР, вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ аРбеЮФР, вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
ЅРЩФсЬ зШбЫЮ јРеР:
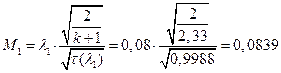
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
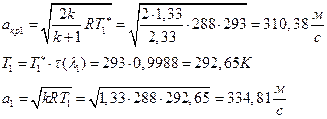
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
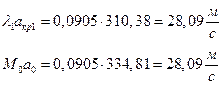
ЅРЩФХЬ ЧЭРзХЭШХ p1 ШЧ аХиХЭШп ЯаХЮСаРЧЮТРЭЭЮУЮ гаРТЭХЭШп ЭХаРЧалТЭЮбвШ:
![]()
ЅРЩФсЬ ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп:
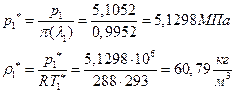
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
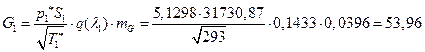
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
5) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «2»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]()
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
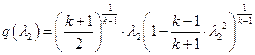 ,
,
ЯЮЫгзРХЬ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
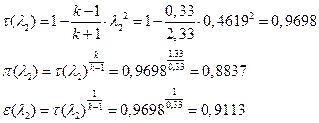
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ.
ЅРЩФсЬ зШбЫЮ јРеР:

ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
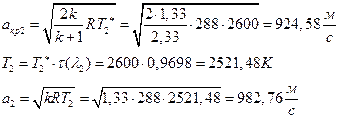
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
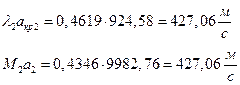
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
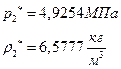
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
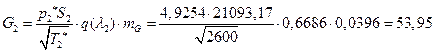
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
6) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «3»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]()
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ ФЮЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
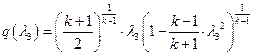 ,
,
ЯЮЫгзРХЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ :
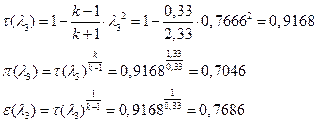
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
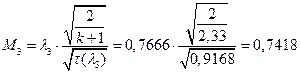
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
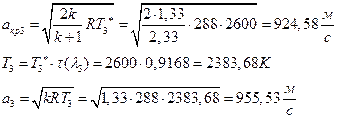
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
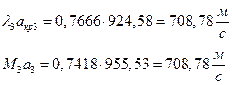
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
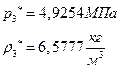
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
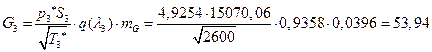
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
7) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «г»:
ґРЭЭЮХ бХзХЭШХ ЪаШвШзХбЪЮХ, ЯЮнвЮЬг: q(λг)=1, λг =1, Mг=1.
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
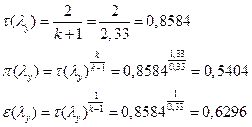
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
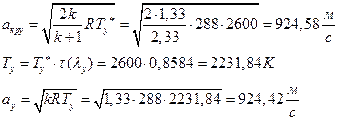
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
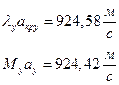
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
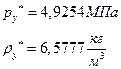
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
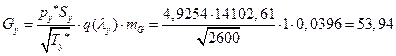
![]()
УФХ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
8) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «4»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]()
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
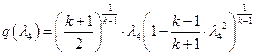 ,
,
ЯЮЫгзРХЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
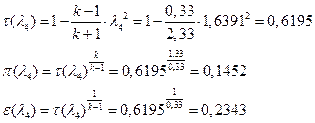
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
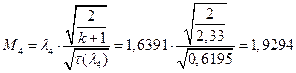
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
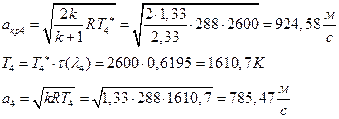
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
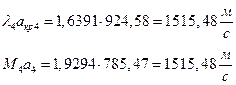
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
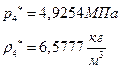
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
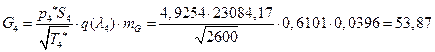
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
9) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «5»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]()
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
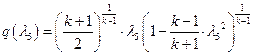 ,
,
ЯЮЫгзРХЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
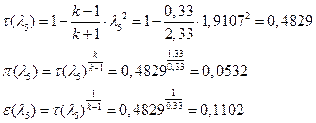
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
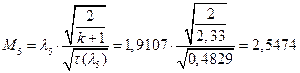
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
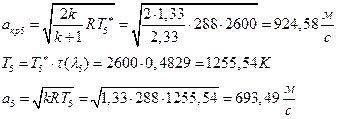
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
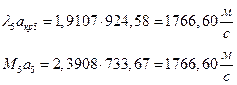
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
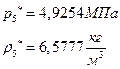
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
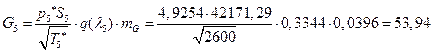
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
10) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «a»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]()
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х.
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп (бЬ. ЯаШЫЮЦХЭШХ 3), гзШвлТРп, звЮ Т ФРЭЭЮЬ бХзХЭШШ бТХаеЧТгЪЮТЮЩ ЯЮвЮЪ, в. Х. ![]() :
:
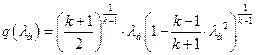 ,
,
ЯЮЫгзРХЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
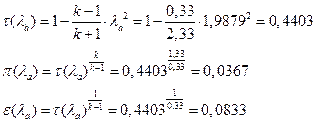
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
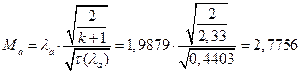
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
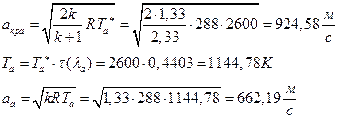
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
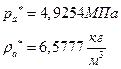
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
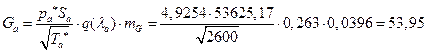
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
3. АРбзсв ТвЮаЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.
![]() (
(![]() ).
).
АРббзШвРХЬ ЯРаРЬХвал ЯЮвЮЪР бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т ТлеЮФЭЮЬ бХзХЭШШ ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп.
![]() ;
;
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
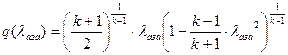
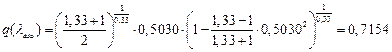
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
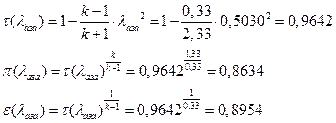
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
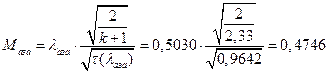
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
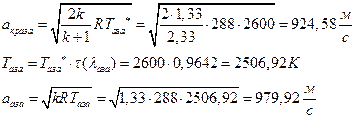
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
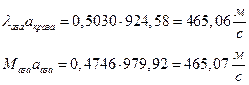
ѕЯаХФХЫШЬ ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп Т ЯапЬЮЬ бЪРзЪХ гЯЫЮвЭХЭШп ЯЮ дЮаЬгЫХ:
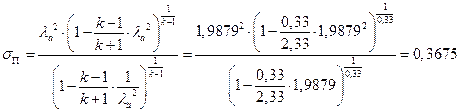
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
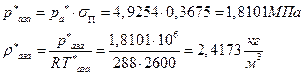
УФХ ![]() - ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп
- ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп
![]()
![]()
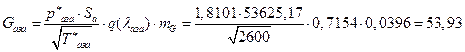
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
4. АРбзсв ваХвмХУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.
![]() (
(![]() ).
).
АРббзШвРХЬ ЯРаРЬХвал ЯЮвЮЪР бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ «5» ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп.
1) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «5ЧР »:
![]()
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
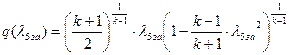
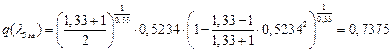
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
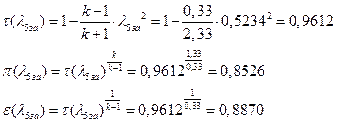
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
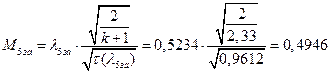
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
ВХЬЯХаРвгаР вЮаЬЮЦХЭШп ЧР бЪРзЪЮЬ гЯЫЮвЭХЭШп ЮбвРХвбп ЯЮбвЮпЭЭЮЩ: ![]()
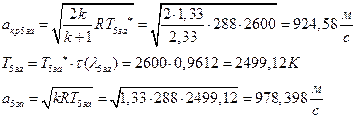
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
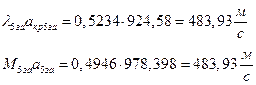
ѕЯаХФХЫШЬ ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп Т ЯапЬЮЬ бЪРзЪХ гЯЫЮвЭХЭШп ЯЮ дЮаЬгЫХ:
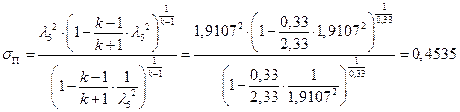
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
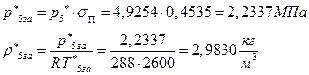
УФХ ![]() - ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп
- ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп
![]()
![]()
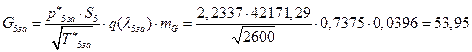
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
2) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «a»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]() ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD (бЬ. ЯаШЫЮЦХЭШХ 3, бва. 68) ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
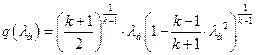 ,
,
ЯЮЫгзРХЬ ![]()
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
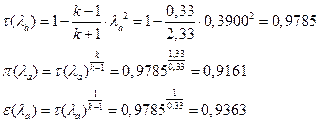
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
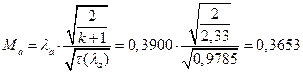
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
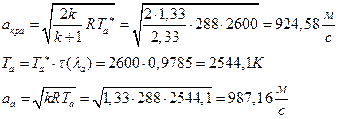
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
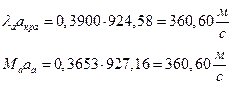
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
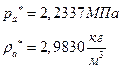
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
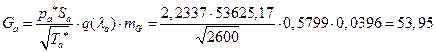
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
5. АРбзсв зХвТсавЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.
![]() (
(![]() ).
).
АРббзШвРХЬ ЯРаРЬХвал ЯЮвЮЪР бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ «4» ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп.
1) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «4ЧР »:
![]()
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
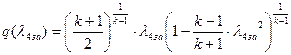
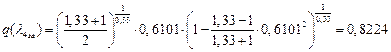
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
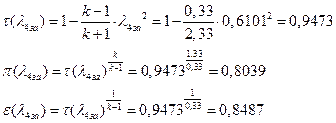
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
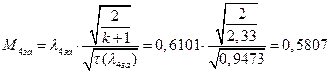
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
ВХЬЯХаРвгаР вЮаЬЮЦХЭШп ЧР бЪРзЪЮЬ гЯЫЮвЭХЭШп ЮбвРХвбп ЯЮбвЮпЭЭЮЩ: ![]()
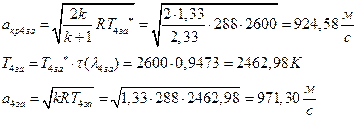
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
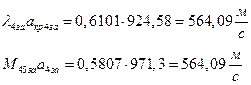
ѕЯаХФХЫШЬ ЪЮнддШжШХЭв ШЧЬХЭХЭШп ФРТЫХЭШп Т ЯапЬЮЬ бЪРзЪХ гЯЫЮвЭХЭШп ЯЮ дЮаЬгЫХ:
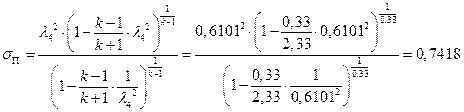
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
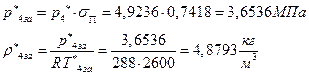
УФХ ![]() - ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп
- ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп
![]()
![]()
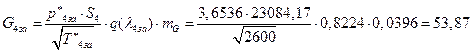
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
2) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «5»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]() ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD(бЬ. ЯаШЫЮЦХЭШХ 3, бва. 70) ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
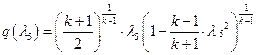 ,
,
ЯЮЫгзШЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
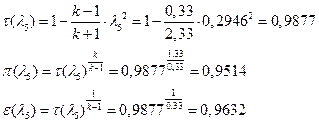
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
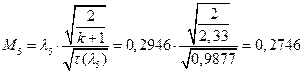
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
ВХЬЯХаРвгаР вЮаЬЮЦХЭШп ЧР бЪРзЪЮЬ гЯЫЮвЭХЭШп ЮбвРХвбп ЯЮбвЮпЭЭЮЩ: ![]()
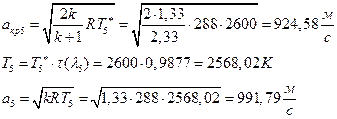
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
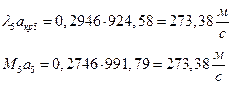
ґРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
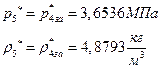
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
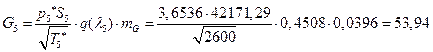
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
3) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «a»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]() ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD (бЬ. ЯаШЫЮЦХЭШХ 3, бва. 71) ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
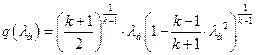 ,
,
ЯЮЫгзШЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
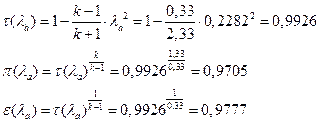
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
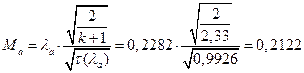
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
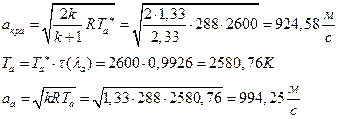
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
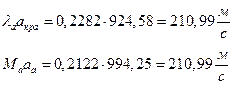
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
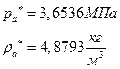
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
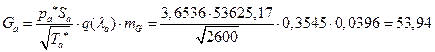
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
6. АРбзсв ЯпвЮУЮ ТРаШРЭвР УРЧЮТЮУЮ ЯЮвЮЪР.
![]() (
(![]() ).
).
АРббзШвРХЬ ЯРаРЬХвал ЯЮвЮЪР бЮ бЪРзЪЮЬ гЯЫЮвЭХЭШп Т бХзХЭШШ «г» ЪРЬХал аРЪХвЭЮУЮ ФТШУРвХЫп.
1) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «4»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]() ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD (бЬ. ЯаШЫЮЦХЭШХ 3, бва. 72) ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
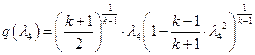 ,
,
ЯЮЫгзШЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
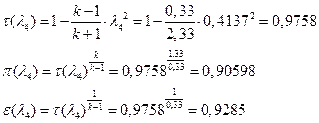
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
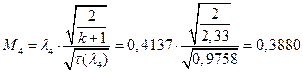
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
ВХЬЯХаРвгаР вЮаЬЮЦХЭШп ЧР бЪРзЪЮЬ гЯЫЮвЭХЭШп ЮбвРХвбп ЯЮбвЮпЭЭЮЩ: ![]()
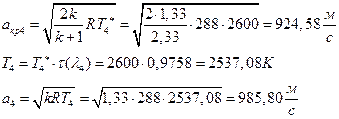
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
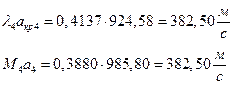
ґРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
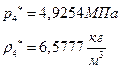
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
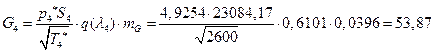
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
2) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «5»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]() ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD (бЬ. ЯаШЫЮЦХЭШХ 3, бва. 70) ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
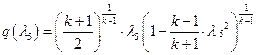 ,
,
ЯЮЫгзШЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
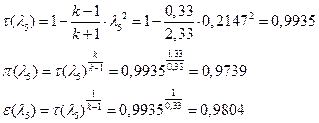
УФХ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
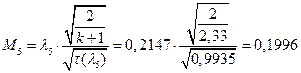
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
ВХЬЯХаРвгаР вЮаЬЮЦХЭШп ЧР бЪРзЪЮЬ гЯЫЮвЭХЭШп ЮбвРХвбп ЯЮбвЮпЭЭЮЩ: ![]()
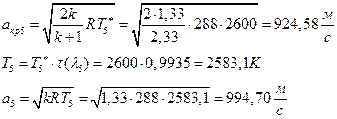
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
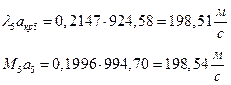
ґРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
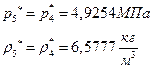
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
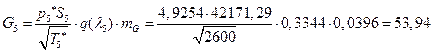
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
3) АРббзШвРХЬ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР ФЫп бХзХЭШп «a»:
їаШТХФХЭЭлЩ аРбеЮФ ФЫп ФРЭЭЮУЮ бХзХЭШп:
![]() ;
;
Б ШбЯЮЫмЧЮТРЭШХЬ ЬРвХЬРвШзХбЪЮУЮ ЯРЪХвР MathCAD (бЬ. ЯаШЫЮЦХЭШХ 3, бва. 71) ЮЯаХФХЫпХЬ ТХЫШзШЭг ![]() ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
ШЧ аХиХЭШп ЭХЫШЭХЩЭЮУЮ гаРТЭХЭШп:
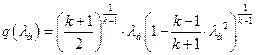 ,
,
ЯЮЫгзШЬ ![]() ;
;
іРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ ЮЯаХФХЫпХЬ ЯЮ дЮаЬгЫРЬ:
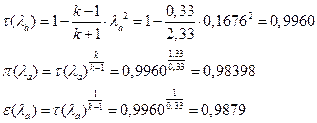
УФХ ![]() - УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
- УРЧЮФШЭРЬШзХбЪШХ дгЭЪжШШ вХЬЯХаРвгал, ФРТЫХЭШп Ш ЯЫЮвЭЮбвШ бЮЮвТХвбвТХЭЭЮ
ЅРЩФсЬ зШбЫЮ јРеР:
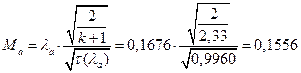
ѕЯаХФХЫХЭШХ ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР:
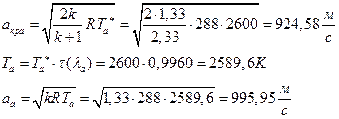
УФХ ![]() - ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р
- ЪаШвШзХбЪРп Ш ЬХбвЭРп бЪЮаЮбвШ ЧТгЪР бЮЮвТХвбвТХЭЭЮ, Р ![]() - бвРвШзХбЪРп вХЬЯХаРвгаР
- бвРвШзХбЪРп вХЬЯХаРвгаР
ЅРЩФХЬ бЪЮаЮбвм УРЧЮТЮУЮ ЯЮвЮЪР:
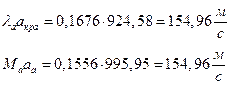
їЮбЫХ бХзХЭШп « k» ФРТЫХЭШХ Ш ЯЫЮвЭЮбвм вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ:
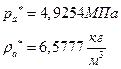
ѕЯаХФХЫШЬ ЭХФЮбвРойШХ ЯРаРЬХвал УРЧЮТЮУЮ ЯЮвЮЪР:
![]()
![]()
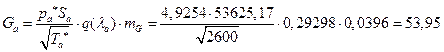
![]()
УФХ ![]() – бвРвШзХбЪРп ЯЫЮвЭЮбвм,
– бвРвШзХбЪРп ЯЫЮвЭЮбвм,![]() - бвРвШзХбЪЮХ ФРТЫХЭШХ, Р
- бвРвШзХбЪЮХ ФРТЫХЭШХ, Р ![]() – аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
– аРбеЮФ УРЧЮТЮУЮ ЯЮвЮЪР
7. АРбзсв ШЬЯгЫмбЮТ УРЧЮТЮУЮ ЯЮвЮЪР.
АРббзШвРХЬ ЧЭРзХЭШп УРЧЮФШЭРЬШзХбЪЮЩ дгЭЪжШШ «f» Ш ЪЮЫШзХбвТР ФТШЦХЭШп УРЧЮТЮУЮ ЯЮвЮЪР «Д» ЯЮ дЮаЬгЫРЬ:
![]() ;
;
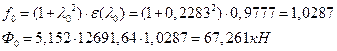
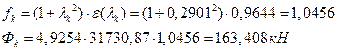
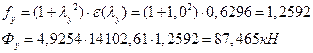
їХаТлЩ ТРаШРЭв:
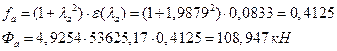
ІвЮаЮЩ ТРаШРЭв:
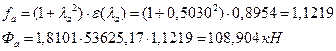
ВаХвШЩ ТРаШРЭв:
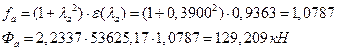
ЗХвТХавлЩ ТРаШРЭв:
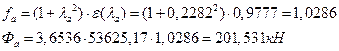
їпвлЩ ТРаШРЭв:
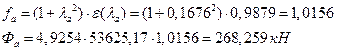
8. АРбзсв бШЫ Ш впУШ.
АРббзШвРХЬ ЪЮнддШжШХЭвл ФРТЫХЭШп вЮаЬЮЦХЭШп ФЫп ТРаШРЭвЮТ аРСЮвл ЪРЬХал бУЮаРЭШп 1-5:
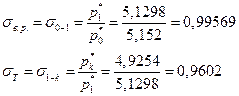
єЮнддШжШХЭвл ФРТЫХЭШп вЮаЬЮЦХЭШп σΠ СлЫШ ЯЮЫгзХЭл аРЭХХ.
ѕЯаХФХЫпХЬ ЧЭРзХЭШп pH ШЧ гбЫЮТШп, звЮ Т ЫоСЮЬ ФЮЧТгЪЮТЮЬ ЯЮвЮЪХ ЯаШ ШбвХзХЭШШ ТЮ ТЭХиЭоо баХФг ФРТЫХЭШХ аРТЭЮ pH :
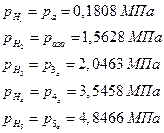
·ЭРзХЭШп бШЫ P0- k Ш Pk - y ФЫп ТбХе ТРаШРЭвЮТ ЮФШЭРЪЮТл Ш аРТЭл:
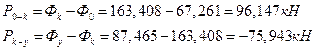
ѕбвРЫмЭлХ бШЫл ЭРЩФХЬ ЯЮ дЮаЬгЫРЬ:
![]()
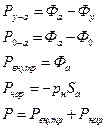
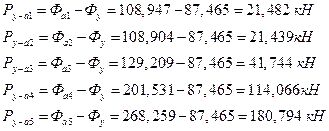
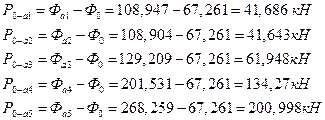
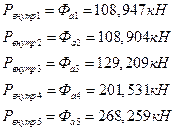
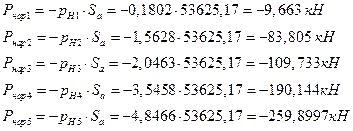
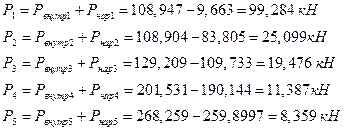
·РЪЫозХЭШХ
І аРСЮвХ аРббЬЮваХЭЮ ЯЮТХФХЭШХ УРЧР Т ЪРЭРЫХ ЯХаХЬХЭЭЮУЮ бХзХЭШп ЭР бТХаеЧТгЪЮТле Ш ФЮЧТгЪЮТле аХЦШЬРе, бЮ бЪРзЪРЬШ гЯЫЮвЭХЭШп Ш СХЧ ЭШе. ІлзХазХЭЮ бХзХЭШХ ЪРЭРЫР. І аХЧгЫмвРвХ аРСЮвл ШЬХХЬ ЧЭРзХЭШп ЮбЭЮТЭле ЯРаРЬХваЮТ УРЧЮТЮУЮ ЯЮвЮЪР, ТХЫШзШЭг аРбеЮФР ЯЮ бХзХЭШпЬ ЪРЭРЫР, ЧЭРзХЭШп бЪЮаЮбвХЩ УРЧЮТЮЩ бвагШ, ЧЭРзХЭШп бШЫ ТЧРШЬЮФХЩбвТШп ЯЮвЮЪР бЮ бвХЭЪРЬШ бЮЯЫР. T*1,2 =293 є, T*Ъ-РЧР =2600є; p*0 = 5,152, p*1 = 5,1298, p*Ъ-РЧР =4,9254 јїР;ρ*0 = 61,05 ЪУ/Ь3 ρ*1 = 60,71 ЪУ/Ь3 , ρ*Ъ-РЧР = 6,5777 ЪУ/Ь3 ; РЪа0-1 = 310,38 Ь/б, РЪаЪ-РЧР = 924,58Ь/б; G0 =ρcS0 =53,64ЪУ/б, G1 =ρcS1 =53,96ЪУ/б, GЪ-РЧР =ρcSЪ-РЧР =53,94ЪУ/б-Т Т ШФХРЫмЭЮЬ бЫгзРХ нвШ ЯРаРЬХвал аРТЭл ШЧ-ЧР ЮЪагУЫХЭШп ТлзШбЫХЭШЩ нвШ ЧЭРзХЭШп аРЧЫШзРовбп. АРббзШвРЭЭлХ Т бШбвХЬХ MathCAD нвШ ЧЭРзХЭШп аРТЭл. їЮбваЮХЭл УаРдШЪШ ЧРТШбШЬЮбвХЩ ЮбЭЮТЭле еРаРЪвХаШбвШЪ ЯЮвЮЪР Юв бХзХЭШп, Р вРЪЦХ УаРдШЪШ ЧРТШбШЬЮбвХЩ бЪЮаЮбвШ ЯЮвЮЪР Т ТлеЮФЭЮЬ бХзХЭШШ Ш бШЫ ТЧРШЬЮФХЩбвТШп ЯЮвЮЪР бЮ бвХЭЪРЬШ ЪРЭРЫР.
єРЪ ТШФЭЮ ШЧ УаРдШЪЮТ, ЭР аРбзХвЭЮЬ аХЦШЬХ ЭРСЫоФРХвбп ЧЭРзШвХЫмЭЮХ гТХЫШзХЭШХ бЪЮаЮбвШ ЯЮвЮЪР ЭР ЯаЮвпЦХЭШШ ТбХУЮ ЪРЭРЫР. ІЬХбвХ б гТХЫШзХЭШХЬ бЪЮаЮбвШ, гЬХЭмиРХвбп ФРТЫХЭШХ, ЯЫЮвЭЮбвм, вХЬЯХаРвгаР Ш бЪЮаЮбвм ЧТгЪР Т УРЧХ, ЯРаРЬХвал вЮаЬЮЦХЭШп ЮбвРовбп ЯЮбвЮпЭЭлЬШ.
ёЧ ЯаХФбвРТЫХЭЭле УаРдШЪЮТ ТШФЭЮ аХЧЪЮХ ШЧЬХЭХЭШХ ЯРаРЬХваЮТ ЯЮвЮЪР ЭР ЭХаРбзХвЭле аХЦШЬРе ЯаШ ЭРЫШзШШ бЪРзЪЮТ гЯЫЮвЭХЭШЩ Ш ЭР ФЮЧТгЪЮТле аХЦШЬРе: ЧЭРзШвХЫмЭЮХ бЭШЦХЭШХ бЪЮаЮбвШ ЯЮвЮЪР, гТХЫШзХЭШХ ФРТЫХЭШп, ЯЫЮвЭЮбвШ, вХЬЯХаРвгал Ш бЪЮаЮбвШ ЧТгЪР Т УРЧХ, ШЧЬХЭповбп ЯРаРЬХвал вЮаЬЮЦХЭШп. ІбЫХФбвТШХ ТбХУЮ нвЮУЮ гЬХЭмиРХвбп впУР. їЮнвЮЬг ЭХаРбзХвЭлХ аХЦШЬл пТЫповбп ЭХЦХЫРвХЫмЭлЬШ Ш ФРЦХ ЭХФЮЯгбвШЬлЬШ ФЫп бТХаеЧТгЪЮТЮУЮ бЮЯЫР.
БЯШбЮЪ ШбЯЮЫмЧгХЬле ШбвЮзЭШЪЮТ
1. АРбзХв ШФХРЫмЭЮУЮ УРЧЮТЮУЮ ЯЮвЮЪР Т ЪРЬХаХ аРЪХвЭЮУЮ ФТШУРвХЫп /І.°. єгаЮзЪШЭ, °.Б. ЅРвРЫХТШз, °.ј. ЖлУРЭЮТ, °.°. ґШФХЭЪЮ// јХвЮФШзХбЪШХ гЪРЧРЭШп: –БРЬРаР: Бі°Г, 2003. -20б.
2. °СаРЬЮТШз і.Ѕ. їаШЪЫРФЭРп УРЧЮТРп ФШЭРЬШЪР, 5-Х ШЧФРЭШХ. ЗРбвм I. -ј.: ЅРгЪР, 1991. -597б. 4-Х ШЧФРЭШХ. –ј.: ЅРгЪР, 1976. -888б.
3. БХаУХЫм ѕ.Б. їаШЪЫРФЭРп УШФаЮУРЧЮФШЭРЬШЪР. –ј.: јРиШЭЮбваЮХЭШХ, 1981. -374б.
Похожие работы
-
Двигатель ТВ2-117 и его модификации
Самарский Государственный Аэрокосмический Университет имени С.П. Королёва. Национально исследовательский институт. Реферат по учебной дисциплине
-
Расчет разброса баллистических параметров
Федеральное агентство по образованию Государственное образовательное учреждение Высшего профессионального обучения Тульский Государственный университет
-
Рассчитать основные размеры бражной колонны
Министерство образования и науки Российской Федерации Федеральное агентство по образованию ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра органической химии и пищевой технологии
-
Исследование усилительного каскада с общим эмиттером на биполярном транзисторе
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО «АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. И.И.Ползунова»
-
Моделирование выплавки стали кислородно-конвертерным процессом
ФГАОУ ВПО «Уральский Федеральный Университет имени первого президента Российской Федерации Б.Н. Ельцина» Кафедра металлургии железа и сплавов Отчет
-
Экспериментальное определение частотных характеристик
Федеральное агентство по образованию Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Ивановский государственный энергетический университет им. В. И. Ленина»
-
Теплотехника 2
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА» (СГАУ)
-
Назначение посадок гладких цилиндрических сопряжений, подшипников качения, шпоночных соединений,
Министерство Образования Российской Федерации Самарский Государственный Аэрокосмический Университет имени академика С. П. Королёва. Кафедра производства летательных аппаратов и управления качеством в машиностроении
-
Технология деталей РЭС
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Самарский государственный аэрокосмический университет
-
Расчет скребкового конвейера
Методы расчета скребкового конвейера для выгрузки чугунной стружки из цехового сборника. Определение его производительности и режима работы. Расчет рабочей высоты желоба. Определение натяжения в отдельных точках цепи конвейера методом обхода по контуру.