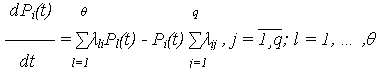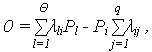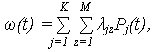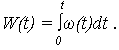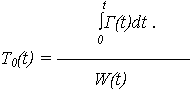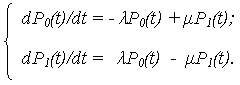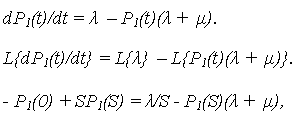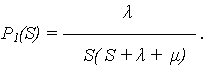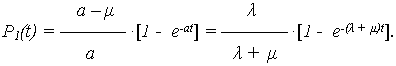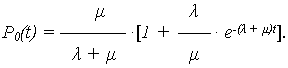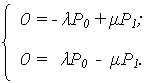Название: Показатели надежности восстанавливаемого объекта

Вид работы: реферат

Рубрика: Информатика

Размер файла: 60.82 Kb

Скачать файл: referat.me-132886.docx

Краткое описание работы: Лекция 13 НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМЫХ ОБЪЕКТОВ И СИСТЕМ 1. Постановка задачи. Общая расчетная модель При расчете показателей надежности восстанавливаемых объектов и систем наиболее распространено

Показатели надежности восстанавливаемого объекта

Лекция 13

НАДЕЖНОСТЬ ВОССТАНАВЛИВАЕМЫХ ОБЪЕКТОВ И СИСТЕМ

1. Постановка задачи. Общая расчетная модель

При расчете показателей надежности восстанавливаемых объектов и систем наиболее распространено допущение:

• экспоненциальное распределение наработки между отказами;
• экспоненциальное распределение времени восстановления.

Допущение во многом справедливо, поскольку во-первых, экспоненциальное распределение наработки описывает функционирование системы на участке нормальной эксплуатации, во-вторых, экспоненциальное распределение описывает процесс без «предыстории».

Применение экспоненциального распределения для описания процесса восстановления позволяет при ординарных независимых отказах представить анализируемые системы в виде марковских систем.

При экспоненциальном распределении наработки между отказами и времени восстановления, для расчета надежности используют метод дифференциальных уравнений для вероятностей состояний (уравнений Колмогорова-Чепмена).

Случайный процесс в какой либо физической системе S , называется марковским, если он обладает следующим свойством: для любого момента t ₀ вероятность состояния системы в будущем (t > t ₀ ) зависит только от состояния в настоящем (t = t ₀ ) и не зависит от того, когда и каким образом система пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса - прошлого).

t < t 0

t > t 0

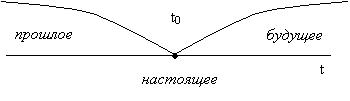
Для марковского процесса «будущее» зависит от «прошлого» только через «настоящее», т. е. будущее протекание процесса зависит только от тех прошедших событий, которые повлияли на состояние процесса в настоящий момент.

Марковский процесс, как процесс без последействия, не означает полной независимости от прошлого, поскольку оно проявляется в настоящем.

При использовании метода, в общем случае, для системы S , необходимо иметь математическую модель в виде множества состояний системы S ₁ , S ₂ , … , S _n , в которых она может находиться при отказах и восстановлениях элементов.

Для рассмотрения принципа составления модели введены допущения:

- отказавшие элементы системы (или сам рассматриваемый объект) немедленно восстанавливаются (начало восстановления совпадает с моментом отказа);

- отсутствуют ограничения на число восстановлений;

- если все потоки событий, переводящих систему (объект) из состояния в состояние, являются пуассоновскими (простейшими), то случайный процесс переходов будет марковским процессом с непрерывным временем и дискретными состояниями S ₁ , S ₂ , … , S _n .

Основные правила составления модели:

1. Математическую модель изображают в виде графа состояний.

Элементы графа:

а) кружки (вершины графа S ₁ , S ₂ , … , S _n ) – возможные состояния системы S , возникающие при отказах элементов;

б) стрелки – возможные направления переходов из одного состояния S_i в другое S_j .

Над/под стрелками указываются интенсивности переходов.

Примеры графа:

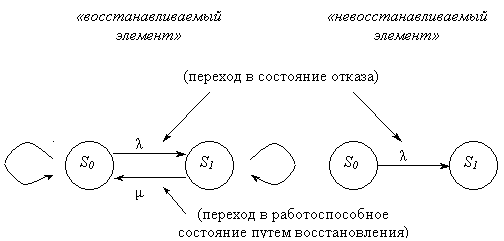
S 0 – работоспособное состояние;

S 1 – состояние отказа.

«Петлей» обозначаются задержки в том или ином состоянии S0 и S1 соответствующие:

- исправное состояние продолжается;

- состояние отказа продолжается (в дальнейшем петли на графах не рассматриваем).

Граф состояний отражает конечное (дискретное) число возможных состояний системы S ₁ , S ₂ , … , S _n . Каждая из вершин графа соответствует одному из состояний.

2. Для описания случайного процесса перехода состояний (отказ/ восстановление) применяют вероятности состояний

P 1 (t), P 2 (t), … , P_i (t), … , P n (t) ,

где P_i (t) – вероятность нахождения системы в момент t в i -м состоянии, т. е.

P_i ( t) = P{ S( t) = si}.

Очевидно, что для любого t

(1)

(нормировочное условие, поскольку иных состояний, кроме S ₁ , S ₂ , … , S _n нет).

3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена), имеющих вид:

(2)

В общем случае, интенсивности потоков _ij и _ij могут зависеть от времени t .

При составлении дифференциальных уравнений пользуются простым мнемоническим правилом:

а) в левой части – производная по времени t от P_i (t);

б) число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;

в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;

г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него.

Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.

4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P 1(t), P_i (t), … , P n(t) необходимо задать начальное значение вероятностей

P 1(0), P_i (0), … , P n(0) , при t = 0 ,

сумма которых равна единице:

Если в начальный момент t = 0 состояние системы известно, например, S(t=0) = Si, то P_i (0) = 1, а остальные равны нулю.

2. Показатели надежности восстанавливаемых систем

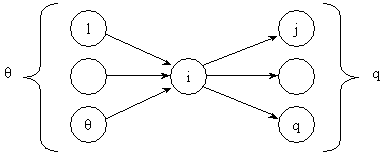
Все состояния системы S можно разделить на подмножества:

SK S – подмножество состояний j = , в которых система работоспособна;

S_M S – подмножество состояний z = , в которых система неработоспособна.

S = S_K S_M ,

S_K S_M = 0.

1. Функция готовности Г(t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t

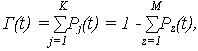
где Pj(t) – вероятность нахождения системы в работоспособном j -м состоянии;

Pz(t) – вероятность нахождения системы в неработоспособном z -м состоянии.

2. Функция простоя П(t) системы

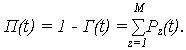
3. Коэффициент готовности kг.с. системы определяется при установившемся режиме эксплуатации (при t ). При t устанавливается предельный стационарный режим , в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются

Коэффициент готовности kг.с. можно рассчитать по системе (2) дифференциальных уравнений, приравнивая нулю их левые части dP_i (t)/dt = 0, т.к. P_i = const при t . Тогда система уравнений (2) превращается в систему алгебраических уравнений вида:

(3)

и коэффициент готовности:

есть предельное значение функции готовности при установившемся режиме t .

4. Параметр потока отказов системы

(4)

где _jz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.

5. Функция потока отказов

(5)

6. Средняя наработка между отказами на интервале t

(6)

Примечание: При t , когда Pj(t = ) = Pj( ) = Pj , средняя наработка между отказами

T ₀ = kг .с ./ ,

где () = .

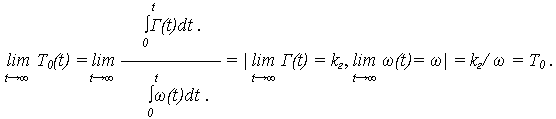
В качестве примера вычисления показателей надежности, рассмотрен восстанавливаемый объект , у которого поток отказов простейший (пуассоновский) с параметром потока

= = 1/ T ₀ ,

а распределение времени восстановления подчиняется экспоненциальному распределению с интенсивностью восстановления

= 1/ T _В ,

где T 0 – средняя наработка между отказами;

T _В – среднее время восстановления.

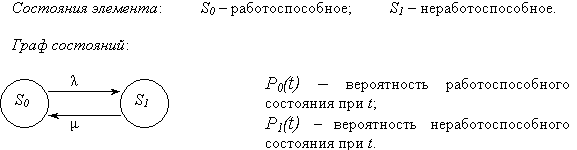
P ₀ (t) – вероятность работоспособного состояния при t ;

P ₁ (t) – вероятность неработоспособного состояния при t.

Система дифференциальных уравнений:

(7)

Начальные условия: при t = 0 P ₀ (t = 0) = P ₀ (0) = 1; P ₁ (0) = 0, поскольку состояния S ₀ и S ₁ представляют полную группу событий, то

P 0 (t) + P 1 (t) = 1.

(8)

Выражая P ₀ (t) = 1 - P ₁ (t) , и подставляя в (7) получается одно дифференциальное уравнение относительно P ₁ (t ):

dP 1 (t)/dt = (1 – P 1 (t)) - P 1 (t).

(9)

Решение уравнения (9) производится с использованием преобразования Лапласа.

Преобразование Лапласа для вероятностей состояния P_i (t):

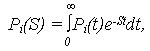
т. е. P_i (S) = L{P_i (t)} – изображение вероятности P_i (t).

Преобразование Лапласа для производной dP_i (t)/dt:

После применения преобразования Лапласа к левой и правой частям уравнения, получено уравнение изображений:

(9)

где L{ } = L{1} = /S .

При P ₁ (0) = 0

SP ₁ (S) + P ₁ (S)( + ) = /S.

P ₁ (S)( S + + ) = /S,

откуда изображение вероятности нахождения объекта в неработоспособном состоянии:

(10)

Разложение дроби на элементарные составляющие приводит к:

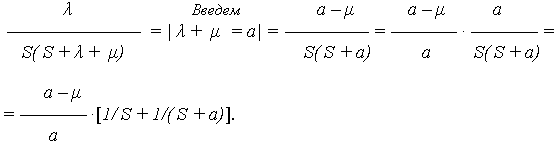
Применяя обратное преобразование Лапласа, с учетом:

L{ f( t)} = 1/ S, то f( t) = 1;

L{ f( t)} = 1/( S + a), то f( t) = e^{- at} ,

вероятность нахождения объекта в неработоспособном состоянии определяется:

(11)

Тогда вероятность нахождения в работоспособном состоянии P0(t) = 1 - P1(t) , равна

(12)

С помощью полученных выражений можно рассчитать вероятность работоспособного состояния и отказа восстанавливаемого объекта в любой момент t .

Коэффициент готовности системы kг.с.. определяется при установившемся режиме t , при этом P_i (t) = P_i = const , поэтому составляется система алгебраических уравнений с нулевыми левыми частями, поскольку

dP_i (t)/dt = 0.

Так как kг.с есть вероятность того, что система окажется работоспособной в момент t при t , то из полученной системы уравнений определяется P0 = kг.с .

При t алгебраические уравнения имеют вид:

(13)

Дополнительное уравнение: P0 + P ₁ = 1.

Выражая P ₁ = 1 - P ₀ , получаем 0 = P ₀ - (1 - P ₀ ), или = P ₀ ( + ), откуда

(14)

Остальные показатели надежности восстанавливаемого элемента:

- функция готовности Г(t), функция простоя П(t)

Г (t) = P ₀ (t); П (t) = 1 - Г (t) = P ₁ (t) .

- параметр потока отказов (t) по (4)

(t) = P ₀ (t) = Г(t).

При t (стационарный установившийся режим восстановления)

( t) = () = = P0 = kг.с.

- ведущая функция потока отказов (t )

- средняя наработка между отказами (t )

t₀ = kг.с./ = kг.с./ kг = 1/ .

На рис. приведено изменение вероятности нахождения объекта в работоспособном состоянии.

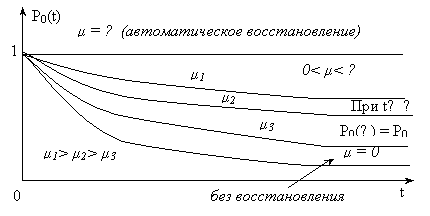
Рис. 1

Анализ изменения P ₀ (t) позволяет сделать выводы:

1) При мгновенном (автоматическом) восстановлении работоспособности (= )

/ = 0 и P0(t) = 1.

2) При отсутствии восстановления ( = 0)

/ = и P0(t) = e^-t ,

и вероятность работоспособного состояния объекта равна ВБР невосстанавливаемого элемента.

Некоторые дополнения по применению метода дифференциальных уравнений для оценки надежности.

Метод дифференциальных уравнений может быть использован для расчета показателей надежности и невосстанавливаемых объектов (систем).

В этом случае неработоспособные состояния системы являются «поглощающими» и интенсивности выхода из этих состояний исключаются.

Для невосстанавливаемого объекта граф состояний имеет вид:

Система дифференциальных уравнений:

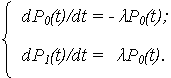
Начальные условия: P ₀ (0) = 1; P ₁ (0) = 0.

Изображение по Лапласу первого уравнения системы:

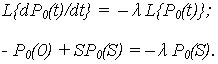
После группировки:

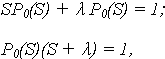
откуда

Используя обратное преобразование Лапласа, оригинал вероятности нахождения в работоспособном состоянии, т. е. ВБР к наработке t :

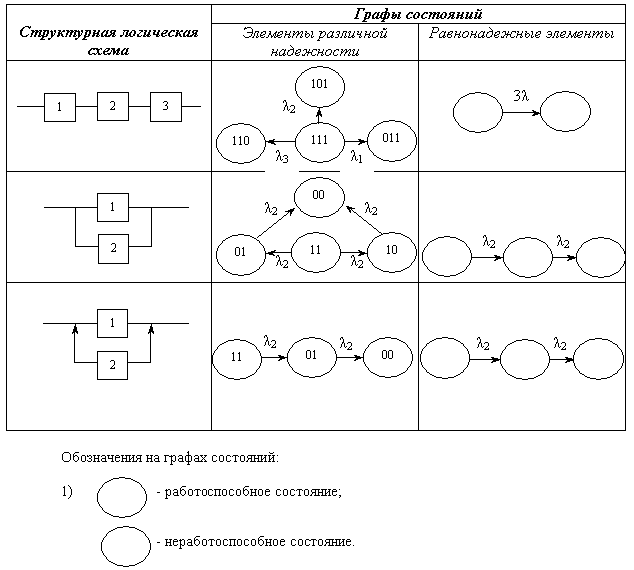
3. Связь логической схемы надежности с графом состояний

Переход от логической схемы к графу состояний необходим:

1)при смене методов расчета надежности и сравнении результатов;

2) для оценки выигрыша в надежности при переходе от невосстанавливаемой системы к восстанавливаемой.

Рассмотрим типовые логические структуры надежности. Типовые соединения рассмотрены для невосстанавливаемых систем (граф – однонаправленный, переходы характеризуются ИО ).

Для восстанавливаемых систем в графах состояний добавляются обратные стрелки, соответствующие интенсивностям восстановлений .