Название: Економіко-математична модель оптимізації структури посівних площ

Вид работы: реферат

Рубрика: Информатика

Размер файла: 44.27 Kb

Скачать файл: referat.me-132919.docx

Краткое описание работы: Задача 5. Економіко-математична модель оптимізації структури посівних площ. Загальна постановка задачі В сільському господарстві земля - основний засіб виробництва. Її необхідно використовувати з максимальним економічним ефектом, постійно дбаючи про родючість. Успішне рішення задачі раціонального використання землі багато в чому залежить від обґрунтованої структури посівних площ.

Економіко-математична модель оптимізації структури посівних площ

Задача 5.

Економіко-математична модель оптимізації структури посівних площ.

Загальна постановка задачі

В сільському господарстві земля - основний засіб виробництва. Її необхідно використовувати з максимальним економічним ефектом, постійно дбаючи про родючість. Успішне рішення задачі раціонального використання землі багато в чому залежить від обґрунтованої структури посівних площ.

Оптимальна структура посівних площ являє собою відображення спеціалізації рослинництва у вигляді такого співвідношення посівних площ по культурах, яке забезпечує отримання максимальної кількості сільськогосподарської продукції.

Постановка задачі: виходячи з виробничих ресурсів (земельних, трудових, матеріальних, тощо) визначити оптимальну структуру посівних площ, яка забезпечить виконання плану продажу продукції по видах, внутрішні потреби господарства в продукції, агрономічні та сівозмінні вимоги при максимальному економічному ефекті.

В якості критерію оптимальності може бути:

- максимум отримання прибутку від виробництва;

- максимум виробництва валової та товарної продукції в грошовому виразі;

- максимум виробництва конкретної продукції (зерна, картоплі, тощо).

Для розробки економіко-математичної моделі необхідна така інформація:

- розмір площі ріллі, сінокосів, пасовищ;

- перелік сільськогосподарських культур, що вирощуються в даній кліматичній зоні, їх можлива врожайність;

- затрати праці та коштів на 1га посіву;

- виручка від реалізації продукції (з 1га або одиниці продукції);

- наявність виробничих ресурсів в господарстві, норми витрат їх на 1га;

- потреба тварин в кормах по видах;

- план продажу та внутрішня потреба господарства по видах продукції;

- агротехнічні вимог та можливі межі входження окремої культури або групи культур в сівозміну.

Економіко-математичну модель можна представити в загальному виді.

Знайти максимум функції:

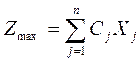
при обмеженнях:

- виробничі ресурси господарства обмежені:

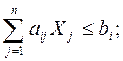
- окремі культури та групи культур в сівозміну вводяться в обґрунтованих агротехнічними вимогами межах:

;

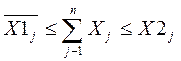- дотримується співвідношення окремих культур (наприклад: для отримання збалансованих концентрованих кормів, страхові культури, ...):

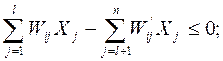
- обмеження, на отримання продукції даного виду не менше заданої кількості:

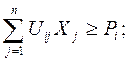
- при умові невід’ємності змінних:

де:

- прибуток з 1га j -ї культури;

- площа посіву j -тої культури;

- затрати ресурсів i -го виду на 1га j -ї культури;

- наявність виробничих ресурсів i -го виду;

- нижня межа входження окремої культури або групи культур в сівозміну;

- верхня межа входження окремої культури або групи культур в сівозміну;

- урожайність j -тої культурі;

- необхідна кількість i -го виду продукції;

- коефіцієнти пропорційності.

Умова задачі

Господарство має 1200га оранки, на яких може вирощувати зернові та просапні культури.

Площа зернових у структурі посівних площ повинна бути від 40 до 60%, площа цукрових буряків не повинна перевищувати 15%, а площа соняшника або картоплі – не більше 10%. Площа озимих повинна бути не більше 50% від максимальної площі зернових. Площа ярої пшениці співвідноситься до площі озимої пшениці як 1:10.

Підприємство повинно виробити не менше:

- 15600ц зерна (в тому числі 7050ц пшениці);

- 10500ц цукрового буряку;

- 1050ц соняшника;

- 530ц проса або гречки.

Крім цього для галузі тваринництва необхідно:

- соломи – 17400ц;

- кукурудзи на силос (зелений корм) – 15570ц

В якості критерію оптимальності виступає прибуток від товарної продукції рослинництва.

Культури для розробки економіко-математичної моделі наведено в таблиці 7, вихідні дані взяти довільно з заданого діапазону (таблиця 1).

Розробити економіко-математичну модель, змінними в якій будуть площі під кожну культуру (Х ₁ , Х ₂ , ..., Х ₈ ), валові збори культур (Х ₉ , Х ₁₀ , ..., Х ₁₆ ), загальні витрати на виробництво продукції (Х ₁₇ ), витрати на виробництво товарної продукції (Х ₁₈ ), виручка від реалізації товарної продукції рослинництва (Х ₁₉ ).

Таблиця 1

Культури, що будуть висіватися в господарстві

Варіант	Зернові					Просапні
3	озима пшениця	яра пшениця	ячмінь	гречка	просо	цукровий буряк	соняшник	кукурудза на з/к

Таблиця 2

Вихідні дані для розробки економіко-математичної моделі

Культура	Урожайність, ц/га		Затрати на 1 га, грн.	Ціна реалізації 1ц, грн.
	основна продукція	побічна продукція
Озима пшениця	45	55	600	40
Яра пшениця	30	30	480	40
Гречка	12	480	44
Ячмінь	35	35	300	38
Просо	20	25	450	29
Цукровий буряк	280	2300	16
Соняшник	23	650	90
Кукурудза на з/к	250	300

Рішення

На 19-ть змінних задачі накладено 25 обмежень:

1-ше обмеження стосується використання наявної площі:

1X ₁ +1X ₂ +1X ₃ +1X ₄ +1X ₅ +1X ₆ +1X ₇ +1X ₈ <=1200, де:

X ₁ ,X ₂ , ..., X ₈ – площі сільськогосподарських культур.

2-ге та 3-тє обмеження задають верхню та нижню межу насиченості сівозміни зерновими культурами, питома вага яких повинна бути від 40% до 60%.

1X ₁ +1X ₂ +1X ₃ +1X ₄ +1X ₅ £720 (60%)

1X ₁ +1X ₂ +1X ₃ +1X ₄ +1X ₅ ³480 (40%), де

X ₁ ,X ₂ ,X ₃ ,X ₄ ,X ₅ – площі зернових культур.

4-те, 5-те та 6-те обмеження описують максимальну площу цукрових буряків, озимих та картоплі відповідно, так 4-те стосується площі цукрових буряків:

1X ₆ £180 (15%), де:

X ₆ – площа цукрових буряків.

7-ме обмеження характеризує співвідношення між площею посіву озимої пшениці та ярої пшениці:

1X ₁ -10X ₂ =0, де:

X ₁ – площа озимої пшениці;

X ₂ – площа ярої пшениці.

Група обмежень з 8-го по 12-те задають нижню межу виробництва певної продукції, так 8-ме обмеження характеризується валового збору зерна, який повинен бути на менше 15600 ц:

1X ₉ +1X ₁₀ +1X ₁₁ +1X ₁₂ +1X ₁₃ >=15600; де:

X ₉ ,X ₁₀ ,X ₁₁ ,X ₁₂ ,X ₁₃ – валові збори озимої пшениці, ярої пшениці, гречки, жита, гороху відповідно.

13-те та 14-те обмеження забезпечать задоволення потреб тваринництва в соломі та силосі відповідно, так 13-те має вигляд:

55X ₁ +30X ₂ +35X ₄ +25X ₅ >=17400; де:

X ₁ ,X ₂ ,X ₄ ,X ₅ – площі зернових культур: озимої пшениці, ярої пшениці, жита та гороху відповідно (коефіцієнти при цих змінних - урожайність соломи відповідних культур).

Обмеження з 15-го по 22-ге забезпечують зв’язок між площею посіву та валовим збором по кожній сільськогосподарській культурі, 15-те обмеження стосується озимої пшениці:

45 X ₁ -X ₉ =0; де:

X ₁ – площа озимої пшениці (32 – урожайність озимої пшениці);

X ₉ – валовий збір озимої пшениці.

23-те обмеження акумулює затрати на виробництво продукції:

600X ₁ +480X ₂ +30X ₃ +480X ₄ +450X ₅ +2300X ₆ +650X ₇ +300X ₈ – X 17=0; де:

X ₁ ,X ₂ , ..., X ₈ – площі сільськогосподарських культур (коефіцієнти при змінних – затрати на 1 га, грн.);

X ₁₇ – загальні затрати на виробництво продукції, грн.

24-те обмеження характеризує затрати на виробництво товарної продукції:

600X ₁ +480X ₂ +30X ₃ +480X ₄ +450X ₅ +2300X ₆ +650X ₇ – X 18=0; де:

X ₁ ,X ₂ , X ₃ , X ₄ , X ₅ , X ₆ , X ₇ – площі товарних сільськогосподарських культур (коефіцієнти при змінних – затрати на 1 га, грн.);

X ₁₈ – загальні затрати на виробництво товарної продукції, грн.

25-те обмеження стосується виручки від реалізації товарної продукції:

40X ₉ +40X ₁₀ +38X ₁₁ +44X ₁₂ +29X ₁₃ +16X ₁₄ +90X ₁₅ -X ₁₉ =0; де:

X ₉ ,X ₁₀ ,X ₁₁ ,X ₁₂ ,X ₁₃ ,X ₁₄ ,X ₁₅ – валові збори с/г культур (коефіцієнти при змінних – ціна реалізації 1 ц продукції, грн.);

X ₁₉ – виручка від реалізації товарної продукції рослинництва, грн.

В якості критерію оптимальності виступає прибуток від виробництва товарної продукції рослинництва:

1X ₁₉ –1X ₁₈ -max.

Економіко-математичну модель оптимізації посівних площ можна представити в табличному вигляді.

Економіко-математична модель оптимізації структури посівних площ
№	Площі с/г культур, га								Валовий збір, ц								Затрати на виробництво продукції, грн.	Затрати на виробництво товарної продукції, грн.	Виручка від реалізації товарної продукції, грн.	Тип та розмір обмежень		№
	Озимої пшениці	Ярої пшениці	Гречки	Жита	Гороху	Цукрового буряку	Картоплі	Кукурудзи на силос	Озимої пшениці	Ярої пшениці	Гречки	Жита	Гороху	Цукрового буряку	Картоплі	Кукурудзи на силос
Змінні	х1	х2	х3	х4	х5	х6	х7	х8	х9	х10	х11	х12	х13	х14	х15	х16	х17	х18	х19
Обмеження
1.	Площа ріллі	1	1	1	1	1	1	1	1	<=	1200	1
2.	Площа зернових max	1	1	1	1	1	<=	720	2
3.	Площа зернових min	1	1	1	1	1	>=	480	3
4.	Площа цукрових буряків	1	<=	180	4
5.	Площа озимих	1	<=	360	5
6.	Площа картоплі	1	<=	120	6
7.	Співвідношення площі ярої пшениці до площі озимої	1	-10	=	0	7
8.	Збір зерна	1	1	1	1	1	>=	15600	8
9.	Збір пшениці	1	1	>=	7050	9
10.	Збір цукрового буряку	1	>=	10500	10
11.	Збір гречки	1	>=	530	11
12.	Збір картоплі	1	>=	8720	12
13.	Потреба тваринництва в соломі	40	30	25	16	>=	17400	13
14.	Потреба тваринництва в силосі	178	>=	15570	14
15.	Виробництво пшениці озимої	32	-1	=	0	15
16.	Виробництво пшениці ярої	30	-1	=	0	16
17.	Виробництво гречки	9	-1	=	0	17
18.	Виробництво жита	25	-1	=	0	18
19.	Виробництво гороху	16	-1	=	0	19
20.	Виробництво цукрового буряку	226	-1	=	0	20
21.	Виробництво картоплі	190	-1	=	0	21
22.	Виробництво кукурудзи	178	-1	=	0	22
23.	Витрати на виробництво продукції	540	320	380	356	397	1865	1921	302	-1	=	0	23
24.	Затрати на виробництво товарної продукції	540	320	380	356	397	1865	1921	-1	=	0	24
25.	Виручка від реалізації товарної продукції	40	40	44	28	45	16	50	-1	=	0	25
Цільова функція (прибуток), грн.		-1	1	max