Название: Построение и анализ на чувствительность моделей задач линейного программирования
Вид работы: лабораторная работа
Рубрика: Информатика
Размер файла: 26.34 Kb
Скачать файл: referat.me-133682.docx
Краткое описание работы: Лабораторная работа №1 ПОСТРОЕНИЕ И АНАЛИЗ НА ЧУВСТВИТЕЛЬНОСТЬ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Цель работы: научиться определять оптимальный план производства (приобретения) продукции с учетом ограниченного обеспечения ресурсами различного вида; освоить методику и технологию поиска оптимального решения задач линейного программирования (ЗЛП) с помощью ЭВМ; приобрести практический опыт проведения анализа оптимального решения ЗЛП на чувствительность.
Построение и анализ на чувствительность моделей задач линейного программирования
Лабораторная работа №1
ПОСТРОЕНИЕ И АНАЛИЗ НА ЧУВСТВИТЕЛЬНОСТЬ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Цель работы: научиться определять оптимальный план производства (приобретения) продукции с учетом ограниченного обеспечения ресурсами различного вида; освоить методику и технологию поиска оптимального решения задач линейного программирования (ЗЛП) с помощью ЭВМ; приобрести практический опыт проведения анализа оптимального решения ЗЛП на чувствительность.
Вариант 1. Для изготовления обуви четырех моделей на фабрике используются два сорта кожи. Ресурсы рабочей силы и материала, затраты труда и материала для изготовления каждой пары обуви, а также прибыль от реализации единицы продукции приведены в таблице. Составить план выпуска обуви по ассортименту, максимизирующий прибыль.
| Ресурсы | Запас ресурса | Затраты ресурсов на одну пару обуви по моделям | |||
| № 1 | № 2 | № 3 | № 4 | ||
Рабочее время, чел.-ч Кожа 1-го сорта Кожа 2-го сорта |
1000 500 1200 |
1 2 0 |
2 1 1 |
2 0 4 |
1 0 1 |
| Прибыль, ден. ед. | 2 | 40 | 10 | 15 | |
Х1 – количество обуви модели №1, выпускаемое фабрикой;
Х2 – количество обуви модели №2, выпускаемое фабрикой;
Х3 – количество обуви модели №3, выпускаемое фабрикой;
Х4 – количество обуви модели №4, выпускаемое фабрикой.
F = 2*X1 + 40*X2 + 10*X3 + 15*X4 => max - целевая функция
Ограничения на ресурсы:
Х1 + 2*Х2 + 2*Х3 + Х4 ≤ 1000
2*Х1 + Х2 ≤ 500
Х2 + 4*Х3 + Х4 ≤ 1200
Х1 , Х2 ≥ 0
Таблица 1.1.
| Изделия | ЦФ F(X) |
||||||||
| x1 | x2 | x3 | x4 | ||||||
| Оптимальный объем производства | 0 | 500 | 0 | 0 | 20000 | ||||
| Ресурс | Наличие | Расход ресурсов на производство изделий | Общий расход | Остаток | Статус ресурса |
Теневая цена | |||
| x1 | x2 | x3 | x4 | ||||||
| Рабочее время, чел. | 1000 | 0 | 1000 | 0 | 0 | 1000 | 0 | Дефицит | 15 |
| Кожа 1 | 500 | 0 | 500 | 0 | 0 | 500 | 0 | Дефицит | 0 |
| Кожа 2 | 1200 | 0 | 500 | 0 | 0 | 500 | 700 | Излишек | 0 |
Итоговая симплекс-таблица:
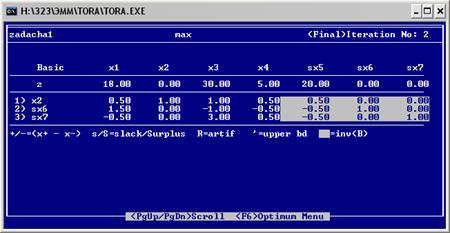
1. Основные вопросы анализа оптимального решения ЗЛП на чувствительность
линейное программирование задача
Основные задачи анализа на чувствительность:
1. Анализ изменений запасов ресурсов позволяет ответить на два вопроса:
а) На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции?
б) На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?
2. Определение наиболее выгодного ресурса, т.е. ресурса, которому следует отдавать предпочтение при инвестировании дополнительных средств.
3. Определение пределов изменения коэффициентов целевой функции делает возможным исследование следующих вопросов:
а) Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?
б) На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным, и, наоборот, дефицитный ресурс сделать недефицитным?
2. Анализ оптимального решения ЗЛП на чувствительность с помощью итоговой симплекс-таблицы
- статус ресурсов:
Ресурс относят к разряду дефицитных, если он израсходован полностью. Недефицитный ресурс, наоборот, имеется в избытке.
- теневая цена:
Для определения наиболее выгодного ресурса вводится характеристика ценности каждой дополнительной единицы дефицитного ресурса
![]() .
.
Решение двойственной задачи yi определяет теневую цену i-го ресурса. Теневая цена ресурса показывает, на сколько увеличится значение целевой функции при увеличении запаса этого ресурса на единицу.
- изменение запасов ресурсов и цены на продукцию:
Объем дефицитного ресурса не следует увеличивать сверх того предела, когда соответствующее ему ограничение становится избыточным. Объем недефицитного ресурса можно уменьшить на величину избытка.
- целесообразность выпуска (приобретения) нового вида продукции
Теневая цена предоставляет возможность оценить целесообразность введения в оптимальный план продукцию нового вида. Если выполняется условие
![]()
то введение в план j-го вида продукции выгодно.
Вывод
В данной лабораторной работе я научилась определять оптимальный план производства (приобретения) продукции с учетом ограниченного обеспечения ресурсами различного вида; освоила методику и технологию поиска оптимального решения задач линейного программирования (ЗЛП) с помощью ЭВМ; приобрела практический опыт проведения анализа оптимального решения ЗЛП на чувствительность.
Похожие работы
-
Задач линейного программирования
Цель работы: изучить теорию и методы решения задач линейного программирования; пробрести навыки построения моделей линейного программирования и решения задач линейного программирования на ЭВМ.
-
Нахождение оптимального плана производства продукции с использованием пакетов прикладных программ
СОДЕРЖАНИЕ Глава 1. Задание Цель курсовой работы Исходные данные Глава 2. Ознакомительный курс исследования операций Введение Линейное программирование
-
Решение задачи оптимального резервирования системы методом динамического программирования
Надежность АСО и У Лабораторная работа № 3 Решение задачи оптимального резервирования системы методом динамического программирования Вариант №1 Студент
-
Разработка подсистемы управления оптимального плана выпуска изделий
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ ТАДЖИКИСТАН ТАДЖИКСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени академика М.С. Осими Кафедра: «АСОИ и У» ОТЧЕТ по лабораторной работе
-
Решение задач линейного программирования различными методами
Контрольная работа Задание 1 Решение задач линейного программирования графическим методом Цель задания: приобрести практические навыки решения задач линейного программирования графическим методом.
-
Программирование линейных алгоритмов
Реферат по теме: «» Ученика 9-г класса средней школы №150 МОУ СОШ г. Челябинска Бологова Дениса 2011г. Содержание. Понятие алгоритмических структур.
-
Решение задач линейного программирования 3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «БРЕСТСКИЙ ГОСУДАОСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра информатики и прикладной математики
-
Транспортная задача 5
Содержание Введение Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических обработках и практическом применении на транспорте и в промышленности. Особенно важное значение она имеет в деле рационализации постановок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.
-
Задачи линейного программирования 2
Лабораторная работа. Тема Задачи линейного программирования Цель: преобретение практических навыков применения методов линейного программирования
-
Эффективное распределение ресурсов, транспортная задача
Доклад на тему «Эффективное распределение ресурсов. Транспортная задача.» В настоящее время большое прикладное значение имеет задача распределения ресурсов по работам. Значение этой проблемы определяется, во-первых, ограниченностью ресурсов и, во-вторых, тем, что эффективность ресурсов в разных направлениях может быть различна.