Название: Бинарные отношения

Вид работы: реферат

Рубрика: Логика

Размер файла: 29.28 Kb

Скачать файл: referat.me-204270.docx

Краткое описание работы: 1. Бинарные отношения Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных.

Бинарные отношения

1. Бинарные отношения

Бинарные отношения служат простым и удобным аппаратом для весьма широкого круга задач. Язык бинарных и n- арных отношений используется во многих прикладных (для математики) областях, например, таких как математическая лингвистика, математическая биология, математическая теория баз данных. Широкое использование языка бинарных отношений легко объясняется - геометрический аспект теории бинарных отношений есть попросту теория графов.

Введем необходимые определения.

Определение 1.1 . Декартовым произведением множеств X и Y называется множество X xY всех упорядоченных пар (x , y ) таких, что x X , y Y .

Определение 1.2 . Соответствием между множествами X и Y (или соответствием из X в Y ) называется любое подмножество декартова произведения X xY . Если множества X и Y совпадают, то соответствие между множествами X и Y называют также бинарным отношением на множестве X .

Пример 1.1 . Пусть X = {a , b , c , d }, Y = {1 , 2 , 3 , 4 , 5 }. Тогда множество кортежей a={(a , 1 ), (b , 2 ), (c , 3 ), (d , 4 )} являются соответствием из X в Y .

Отметим, что обычно соответствия задаются не путем указания подмножества a декартова произведения X xY , а путем указания свойства пар (x , y ), принадлежащих этому подмножеству

a. Например, отношение a= {(4 , 4 ), (3 , 3 ), (2 , 2 ), (4 , 2 )} на множестве X = {4 , 3 , 2 } можно определить как свойство "Делится" на этом подмножестве целых чисел.

Хорошо известными примерами отношений из школьного курса математики являются:

• на множестве целых чисел Z отношения "делится", "делит", "равно", "больше", "меньше", "взаимно просты";
• на множестве прямых пространства отношения "параллельны", "взаимно перпендикулярны", "скрещиваются", "пересекаются", "совпадают";
• на множестве окружностей плоскости "пересекаются", "касаются", "концентричны".

Факт принадлежности кортежа (x , y ) соответствию a, часто обозначают с помощью так называемой инфиксной формы записи: x ay . Типичными примерами таких записей из курса математики являются: x > y , a = b , 8 4 , m ||l , a b и т. п.

Отношения могут задаваться формулами:

• формулы

y = x² +5x - 6 или

задают бинарные отношения на множестве действительных чисел;

• формула

x + y = любовь,

задает бинарное отношение на множестве людей. Этому отношению принадлежит любая пара людей, между которыми существует любовь.

Задание отношений в виде формул достаточно широко распространено. Об этом свидетельствуют многочисленные надписи на деревьях заборах или стенах домов типа:

"Вася + Таня = любовь",

увековечивающие принадлежность конкретной пары (Вася, Таня) отношению "любовь".

Рассмотрим еще три формы представления бинарных отношений: матричное представление и два графических представления. В качестве носителя отношения для иллюстрирующих примеров будем использовать множество X = {a , b , c , d , e }.

Вначале рассмотрим метод, восходящий к аналитической геометрии. Начертим пару взаимно перпендикулярных осей (OX - горизонтальная ось, а OY - вертикальная ось) и на каждой отметим точки, представляющие элементы множества X (рис. 1).

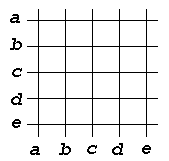
Рис. 1. Координатная сетка

Считая метки a , b , c , d , e координатами точек на горизонтальной и вертикальной осях, отметим на плоскости точки с координатами (x , y ) такими, что (x , y ) . На рисунке 2 изображено множество точек, соответствующее отношению a= {(a , b ), (a , c ), (b , d ), (c , e ), (e ,b ), (e , e )}.

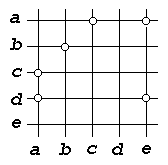
Рис. 2. Бинарное отношение a

Другой широко распространенный способ представления отношений основан на использовании ориентированных графов. При таком представлении элементы множества X изображаются вершинами графа (точками плоскости), а элементы (x , y ) отношения a дугами (стрелками), соединяющими первую компоненту x отношения со второй компонентой y . Граф бинарного отношения a изображен на рисунке 3.

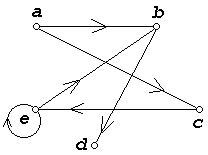
Рис. 3. Граф бинарного отношения

Для бинарных отношений, определенных на конечных множествах, часто используется матричный способ задания. Пусть на некотором конечном множестве X задано отношение a. Упорядочим каким-либо образом элементы множества X = {x₁ , x₂ , ..., x_n } и определим матрицу отношения A = [a_ij ] следующим образом:

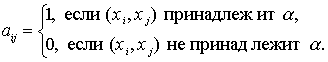
Таким образом, матрица отношения a, представленного графом на рисунке 3, имеет вид

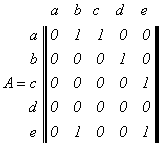
Часто матрицу отношения называют булевой, чтобы подчеркнуть, что ее элементами являются только нули и единицы.