Название: Определение оптимальной цены

Вид работы: реферат

Рубрика: Маркетинг

Размер файла: 54.12 Kb

Скачать файл: referat.me-210343.docx

Краткое описание работы: УДК 330.115 Кучма Г.В., научн. руков. ст. пр. Кучма Ю.В. Определение оптимальной цены продажи при экспоненциальном спросе Определена величина оптимальной цены продажи при экспоненциальном спросе. На примере построена функция экспоненциального спроса. Показано, что при определении оптимальной цены на товар, спрос на него можно считать экспоненциальным

Определение оптимальной цены

УДК 330.115

Кучма Г.В., научн. руков. ст. пр. Кучма Ю.В.

Определение оптимальной цены продажи при экспоненциальном спросе

Определена величина оптимальной цены продажи при экспоненциальном спросе. На примере построена функция экспоненциального спроса. Показано, что при определении оптимальной цены на товар, спрос на него можно считать экспоненциальным

Пусть – доля покупателей, имеющих для покупки данного товара в течение некоторого промежутка времени сумму денег . Положим, что каждый из покупателей приобретает одну единицу этого товара, когда его сумма денег , и не купит этот товар в случае . Тогда по цене за то же время будет продано единиц этого товара.

Замечание. При другом поведении покупателей соотношение между и иное. Например, если покупатель при купит ровно единиц товара, тогда

(1)

Определим, что прибыль от продажи единиц товара в течение данного промежутка времени пропорциональна произведению количества проданного товара на разность между ценой и себестоимостью :

(2)

где не зависит от и учитывает возможные издержки, скажем налог на прибыль.

Полагаем , так как – возможные постоянные издержки, влияющие на величину прибыли, но не на оптимальную цену , при которой прибыль максимальна. Будем считать, что для всех точно известна функция – кривая спроса. Величина в общем случае неотрицательная и не возрастает с ростом , а при указанном поведении покупателей пропорциональна .

Значение задает интенсивность (скорость) во времени числа продаж по данной цене . Если интенсивность постоянна, то за период, вдвое больший естественно ожидать и удвоение числа продаж.

Интенсивность может зависеть от времени года, суток и других факторов. Заметим, что задает скорость увеличения прибыли и оптимальная цена обеспечивает ее максимально возможную величину , необходимо найти максимум . Приведем без доказательства следующую теорему.

Теорема: Пусть имеются две функции действительной переменной : линейная и неотрицательная такие, что 1) , где , - произвольные постоянные; 2) принимает неотрицательные значения при , а при удовлетворяет соотношению

(3)

с некоторыми постоянными , , .

Тогда функция достигает строгого глобального максимума на множестве всех действительных чисел в точке и справедливо равенство

Если количество единиц товара которое потребители желают и имеют возможность купить по цене , подчиняется экспоненциальному закону, то есть уменьшается в раз при увеличении цены на , где и не зависят от , а саму цену продавец может устанавливать произвольно, то теорема дает выражение для цены, при которой прибыль максимальна. При такой цене объем продаж составляет или 36.8 % от – возможного объема продаж при нулевой прибыли по цене равной себестоимости (рис. 1).

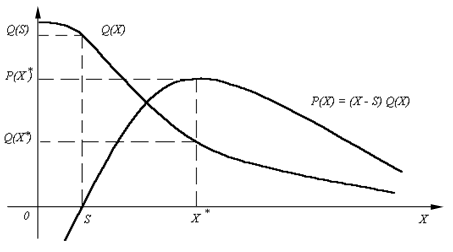
Рисунок 1 Оптимальная цена продажи при экспоненциальном спросе.

Оценим – хвост функции распределения доходов равной отношению количества людей имеющих доход не менее грн., к числу всех рассматриваемых индивидов. Для каждого из таблицы 1 величина равна сумме всех процентов доходов, для которых , например при = 150 грн., .

На рис. 2 изображен график с точками, изображающий - функцию и экспоненциальный тренд аппроксимирующий эти точки.

Использование МНК для логарифмов от дало в классе многочленов от не выше третей степени следующее не возрастающее непрерывное приближение для наблюдаемых значений грн.

Таблица 1 – Распределение дохода в месяц жителей города Киев

Доход человека, грн.	Процент, %	- функция
до 50	27.00	0.97
100	41.00	0.70
150	14.00	0.29
200	9.25	0.15
250	3.00	0.06
более 250	3.00	0.03

Следовательно для хвоста функции распределения населения по величине среднедушевого дохода справедлив закон (3). А если величина спроса , то для также справедливо равенство (3).

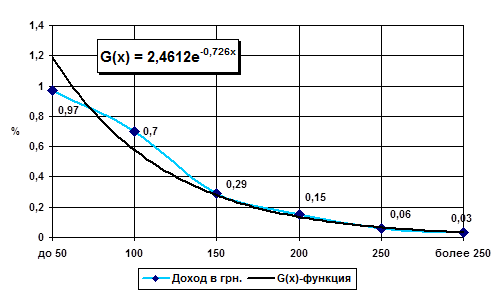
Рисунок 2 G(x) - хвост функции распределения доходов жителей города Киев осенью 1997 г.

Так же при оптимальной цене продажи товара более 150 грн. спрос на него можно считать строго экспоненциальным.

Литература

1. Брыскин В.В. Математические модели маркетинга. – Новосибирск: ВО "Наука", 1992. – 156 с.

2. Цацулин А.Н. Ценообразование в системе маркетинга – М.: Информационно-издательский дом «Филинъ», 1997. – 296 с.