Название: Классические методы безусловной оптимизации
Вид работы: реферат
Рубрика: Математика
Размер файла: 537.09 Kb
Скачать файл: referat.me-214682.docx
Краткое описание работы: ТЕМА Классические методы безусловной оптимизации Введение Как известно, классическая задача безусловной оптимизации имеет вид: Существуют аналитические и численные методы решения этих задач.
Классические методы безусловной оптимизации
ТЕМА
Классические методы безусловной оптимизации
Введение
Как известно, классическая задача безусловной оптимизации имеет вид:
![]() (1)
(1)
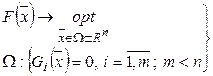 (2)
(2)
Существуют аналитические и численные методы решения этих задач.
Прежде всего вспомним аналитические методы решения задачи безусловной оптимизации.
Методы безусловной оптимизации занимают значительное место в курсе МО. Это обусловлено непосредственным применением их при решении ряда оптимизационных задач, а также при реализации методов решения значительной части задач условной оптимизации (задач МП).
1. Необходимые условия для точки локального минимума (максимума)
Пусть т. ![]() доставляет минимальные значения функции
доставляет минимальные значения функции ![]() . Известно, что в этой точке приращение функции неотрицательно, т.е.
. Известно, что в этой точке приращение функции неотрицательно, т.е.
![]() . (1)
. (1)
Найдем ![]() , используя разложения функции
, используя разложения функции ![]() в окрестности т.
в окрестности т. ![]() в ряд Тейлора.
в ряд Тейлора.
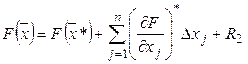 , (2)
, (2)
где 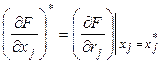 ,
, ![]() ,
, ![]() - сумма членов ряда порядок которых относительно приращений
- сумма членов ряда порядок которых относительно приращений ![]() (двум) и выше.
(двум) и выше.
Из (2) имеем:
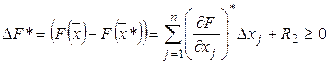 (3)
(3)
Далее предположим, что изменяется только одна переменная из множества переменных ![]() . Например,
. Например, ![]() , тогда (3) преобразуется к виду:
, тогда (3) преобразуется к виду:
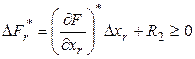 (4)
(4)
Из (4) с очевидностью следует, что
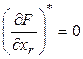 (5)
(5)
Предположим, что 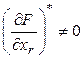 , тогда
, тогда
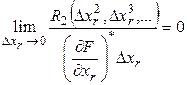 (6)
(6)
С учетом (6) имеем: 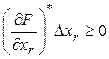 . (7)
. (7)
Предположим, что 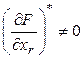 положительно, т.е.
положительно, т.е. 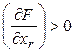 . Выберем при этом
. Выберем при этом ![]() , тогда произведение
, тогда произведение 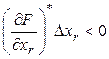 , что противоречит (1).
, что противоречит (1).
Поэтому, действительно, 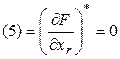 очевиден.
очевиден.
Рассуждая аналогично относительно других переменных ![]() получаем необходимое условие для точек локального минимума функции многих переменных
получаем необходимое условие для точек локального минимума функции многих переменных
![]()
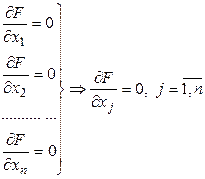 (8)
(8)
Легко доказать, что для точки локального максимума необходимые условия будут точно такими же, как и для точки локального минимуму, т.е. условиями (8).
Понятно, что итогом доказательства будет неравенство вида: ![]() - условие неположительного приращения функции в окрестности локального максимума.
- условие неположительного приращения функции в окрестности локального максимума.
Полученные необходимые условия не дают ответ на вопрос: является ли стационарная точка ![]() точкой минимума или точкой максимума.
точкой минимума или точкой максимума.
Ответ на этот вопрос можно получить, изучив достаточные условия. Эти условия предполагают исследование матрицы вторых производных целевой функции ![]() .
.
2. Достаточные условия для точки локального минимума (максимума)
Представим разложение функции ![]() в окрестности точки
в окрестности точки ![]() в ряд Тейлора с точностью до квадратичных по
в ряд Тейлора с точностью до квадратичных по ![]() слагаемых.
слагаемых.
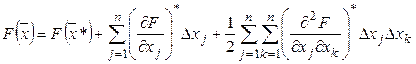 (1)
(1)
Разложение (1) можно представить более кратко, используя понятие: "скалярное произведение векторов" и "векторно-матричное произведение".
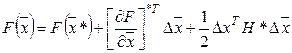 (1')
(1')
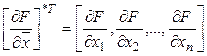
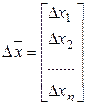
![]()
![]() - матрица двух производных от целевой функции по соответствующим переменным.
- матрица двух производных от целевой функции по соответствующим переменным.
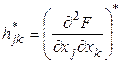 ,
, ![]()
Приращение функции ![]() на основании (1') можно записать в виде:
на основании (1') можно записать в виде:
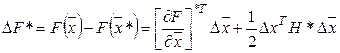 (3)
(3)
Учитывая необходимые условия:
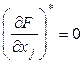 ,
, ![]() (4)
(4)
Подставим (3) в виде:
![]() (4')
(4')
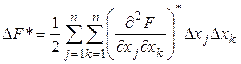 (5)
(5)
Квадратичная форма ![]() называется дифференциальной квадратичной формой (ДКФ).
называется дифференциальной квадратичной формой (ДКФ).
Если ДКФ положительно определена, то ![]() и стационарная точка
и стационарная точка ![]() является точкой локального минимума.
является точкой локального минимума.
Если же ДКФ и матрица ![]() , ее представляющая, отрицательно определены, то
, ее представляющая, отрицательно определены, то ![]() и стационарная точка
и стационарная точка ![]() является точкой локального максимума.
является точкой локального максимума.
Итак, необходимое и достаточное условие для точки локального минимума имеют вид
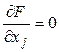
![]() (эти же необходимые условия можно записать так:
(эти же необходимые условия можно записать так:
![]() ,
, ![]() ,
, ![]() )
)
![]() - достаточное условие.
- достаточное условие.
Соответственно, необходимое и достаточное условие локального максимума имеет вид:
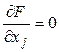 ,
, ![]() (
(![]() ),
), ![]() .
.
Вспомним критерий, позволяющий определить: является ли квадратичная форма и матрица, ее представляющая, положительно определенной, или отрицательно определенной.
3. Критерий Сильвестра
Позволяет ответить на вопрос: является ли квадратичная форма и матрица, ее представляющая, положительно определенной, или отрицательно определенной.
Далее изложение будет относительно ДКФ и матрицы ![]() ее определяющей, т.е. ДКФ вида
ее определяющей, т.е. ДКФ вида
![]() .
.
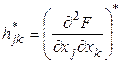 ,
, ![]() - называется матрицей Гессе.
- называется матрицей Гессе.
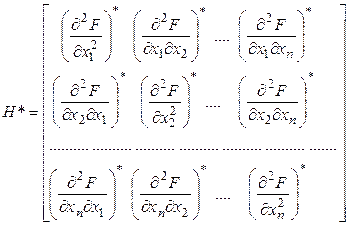
Главный определитель матрицы Гессе ![]()
![]()
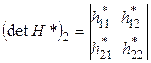
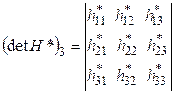
![]()
![]() и ДКФ, которую оно представляет, будут положительно определенными, если все главные определители матрицы Гессе (
и ДКФ, которую оно представляет, будут положительно определенными, если все главные определители матрицы Гессе (![]() ) положительны (т.е. имеет место следующая схема знаков:
) положительны (т.е. имеет место следующая схема знаков:
![]() )
)
Если же имеет место другая схема знаков для главных определителей матрицы Гессе ![]() , например,
, например, ![]() , то матрица
, то матрица ![]() и ДКФ отрицательно определены.
и ДКФ отрицательно определены.
4. Метод Эйлера – классический метод решения задач безусловной оптимизации
Этот метод основан на необходимых и достаточных условиях, изученных в 1.1 – 1.3; применим нахождению локальных экстремумов только непрерывных дифференцируемых функций.
Алгоритм этого метода достаточно прост:
1) используя необходимые условия формируем систему ![]() в общем случае нелинейных уравнений. Отметим, что решить аналитически эту систему в общем случае невозможно; следует применить численные методы решения систем нелинейных уравнений (НУ) (см. "ЧМ"). По этой причине метод Эйлера будет аналитически-численным методом. Решая указанную систему уравнений находим координаты стационарной точки
в общем случае нелинейных уравнений. Отметим, что решить аналитически эту систему в общем случае невозможно; следует применить численные методы решения систем нелинейных уравнений (НУ) (см. "ЧМ"). По этой причине метод Эйлера будет аналитически-численным методом. Решая указанную систему уравнений находим координаты стационарной точки ![]() .;
.;
2) исследуем ДКФ и матрицу Гессе ![]() , которая ее представляет. С помощью критерия Сильвестра определяем, является ли стационарная точка
, которая ее представляет. С помощью критерия Сильвестра определяем, является ли стационарная точка ![]() точкой минимума или точкой максимума;
точкой минимума или точкой максимума;
3) вычисляем значение целевой функции ![]() в экстремальной точке
в экстремальной точке
![]()
Методом Эйлера решить следующую задачу безусловной оптимизации: найти 4 стационарные точки функции вида:
![]()
Выяснить характер этих точек, являются ли они точками минимума, или Седловыми (см. [3]). Построить графическое отображение этой функции в пространстве и на плоскости (с помощью линий уровня).
Далее эту функцию будем именовать типовой функцией, исследуя ее экстремальные свойства всеми изученными методами.
5. Классическая задача условной оптимизации и методы ее решения: Метод исключения и Метод множителей Лагранжа (ММЛ)
Как известно, классическая задача условной оптимизации имеет вид:
![]() (1)
(1)
![]() (2)
(2)
График, поясняющий постановку задачи (1), (2) в пространстве ![]() .
.
![]() (1')
(1')
![]() (2')
(2')
![]() ,
, ![]()
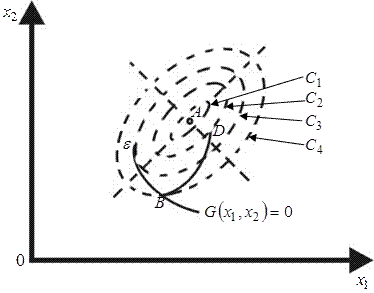
![]() - уравнения линий уровня
- уравнения линий уровня
Итак, ОДР ![]() в рассматриваемой задаче представляет собой некоторую кривую, представленную уравнением (2').
в рассматриваемой задаче представляет собой некоторую кривую, представленную уравнением (2').
Как видно из рисунка, точка ![]() является точкой безусловного глобального максимума; точка
является точкой безусловного глобального максимума; точка ![]() - точкой условного (относительного) локального минимума; точка
- точкой условного (относительного) локального минимума; точка ![]() - точка условного (относительного) локального максимума.
- точка условного (относительного) локального максимума.
Задачу (1'), (2') можно решить методом исключения (подстановки), решив уравнение (2') относительно переменной ![]() , и подставляя найденное решение (1').
, и подставляя найденное решение (1').
![]()
Исходная задача (1'), (2') таким образом преобразована в задачу безусловной оптимизации функции ![]() , которую легко решить методом Эйлера.
, которую легко решить методом Эйлера.
Метод исключения (подстановки).
Пусть целевая функция зависит от ![]() переменных:
переменных:
![]()
![]()
называются зависимыми переменными (или переменными состояния); соответственно можно ввести вектор
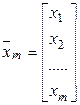
Оставшиеся ![]() переменных
переменных ![]() называются независимыми переменными решения.
называются независимыми переменными решения.
Соответственно можно говорить о вектор-столбце:
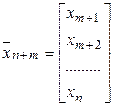 и вектора
и вектора 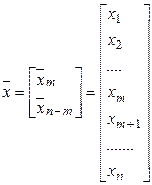 .
.
В классической задаче условной оптимизации:
![]() (1)
(1)
![]() (2)
(2)
Система (2) в соответствии с методом исключения (подстановки) должна быть разрешена относительно зависимых переменных (переменных состояния), т.е. должны быть получены следующие выражения для зависимых переменных:
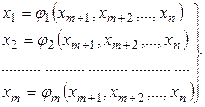 (3)
(3)
Всегда ли система уравнений (2) разрешима относительно зависимых переменных ![]() - не всегда, это возможно лишь в случае, когда определитель
- не всегда, это возможно лишь в случае, когда определитель ![]() , называемый якобианом, элементы которого имеют вид:
, называемый якобианом, элементы которого имеют вид:
![]() ,
, ![]()
не равен нулю (см. соответствующую теорему в курсе МА)
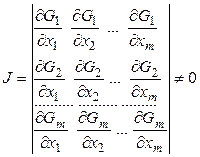
Как видно, функции ![]() ,
, ![]() должны быть непрерывными дифференцируемыми функциями, во-вторых, элементы определителя
должны быть непрерывными дифференцируемыми функциями, во-вторых, элементы определителя ![]() должны быть вычислены в стационарной точке целевой функции.
должны быть вычислены в стационарной точке целевой функции.
Подставляем ![]() из (3) в целевую функцию (1), имеем:
из (3) в целевую функцию (1), имеем:
![]()
![]() (5)
(5)
Исследуемая функция ![]() на экстремум можно произвести методом Эйлера – методом безусловной оптимизации непрерывно дифференцируемой функции.
на экстремум можно произвести методом Эйлера – методом безусловной оптимизации непрерывно дифференцируемой функции.
Итак, метод исключения (подстановки) позволяет использовать задачу классической условной оптимизации преобразовать в задачу безусловной оптимизации функции ![]() - функции
- функции![]() переменных при условии (4), позволяющим получить систему выражений (3).
переменных при условии (4), позволяющим получить систему выражений (3).
Недостаток метода исключения: трудности, а иногда и невозможность получения системы выражений (3). Свободный от этого недостатка, но требующий выполнения условия (4) ![]() является ММЛ.
является ММЛ.
5.2. Метод множителей Лагранжа. Необходимые условия в классической задаче условной оптимизации. Функция Лагранжа ![]()
ММЛ позволяет исходную задачу классической условной оптимизации:
![]() (1)
(1)
![]() (2)
(2)
Преобразовать в задачу безусловной оптимизации специально сконструированной функции – функции Лагранжа:
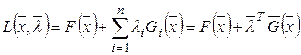 , (3)
, (3)
где ![]() ,
, ![]() - множители Лагранжа;
- множители Лагранжа;
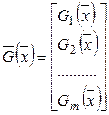 .
.
Как видно, ![]() представляет собой сумму, состоящую из исходной целевой функции
представляет собой сумму, состоящую из исходной целевой функции ![]() и "взвешенной" суммы функций
и "взвешенной" суммы функций ![]() ,
, ![]() - функции, представляющие их ограничения (2) исходной задачи.
- функции, представляющие их ограничения (2) исходной задачи.
Пусть точка ![]() - точка безусловного экстремума функции
- точка безусловного экстремума функции ![]() , тогда, как известно,
, тогда, как известно, 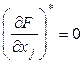 ,
, ![]() , или
, или ![]() (полный дифференциал функции
(полный дифференциал функции ![]() в точке
в точке ![]() ).
).
Используя концепция зависимых и независимых переменных ![]() - зависимые переменные;
- зависимые переменные; ![]() - независимые переменные, тогда представим (5) в развернутом виде:
- независимые переменные, тогда представим (5) в развернутом виде:
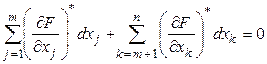 (5')
(5')
Из (2) с очевидностью следует система уравнений вида:
![]() ,
, ![]() (6)
(6)
Результат вычисления полного дифференциала для каждой из функций
![]()
Представим (6) в "развернутом" виде, используя концепцию зависимых и независимых переменных:
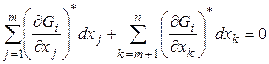 ,
, ![]() (6')
(6')
Заметим, что (6') в отличии от (5') представляет собой систему, состоящую из ![]() уравнений.
уравнений.
Умножим каждое ![]() -ое уравнение системы (6') на соответствующий
-ое уравнение системы (6') на соответствующий ![]() -ый множитель Лагранжа. Сложим их между собой и с уравнением (5') и получим выражение:
-ый множитель Лагранжа. Сложим их между собой и с уравнением (5') и получим выражение:
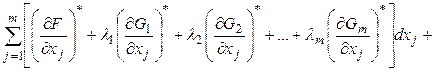
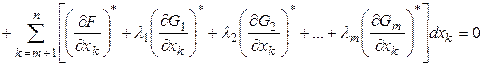 (7)
(7)
Распорядимся множителями Лагранжа ![]() таким образом, чтобы выражение в квадратных скобках под знаком первой суммы (иными словами, коэффициенты при дифференциалах независимых переменных
таким образом, чтобы выражение в квадратных скобках под знаком первой суммы (иными словами, коэффициенты при дифференциалах независимых переменных ![]() ,
, ![]() ) равнялось нулю.
) равнялось нулю.
Термин "распорядимся" множителями Лагранжа вышеуказанным образом означает, что необходимо решить некоторую систему из ![]() уравнений относительно
уравнений относительно ![]() .
.
Структуру такой системы уравнений легко получить приравняв выражение в квадратной скобке под знаком первой суммы нулю:
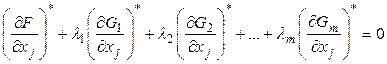 ,
, ![]() (8)
(8)
Перепишем (8) в виде
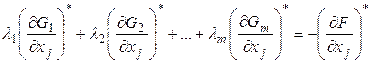 ,
, ![]() (8')
(8')
Система (8') представляет собой систему из ![]() линейных уравнений относительно
линейных уравнений относительно ![]() известных:
известных: ![]() . Система разрешима, если
. Система разрешима, если ![]() (вот почему, как и в методе исключения в рассматриваемом случае должно выполняться условие
(вот почему, как и в методе исключения в рассматриваемом случае должно выполняться условие ![]() ). (9)
). (9)
Поскольку в ключевом выражении (7) первая сумма равна нулю, то легко понять, что и вторая сумма будет равняться нулю, т.е. имеет место следующая система уравнений:
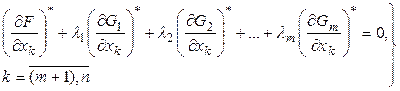 (10)
(10)
Система уравнений (8) состоит из ![]() уравнений, а система уравнений (10) состоит из
уравнений, а система уравнений (10) состоит из ![]() уравнений; всего
уравнений; всего ![]() уравнений в двух системах, а неизвестных
уравнений в двух системах, а неизвестных
![]() :
: ![]() ,
, ![]()
Недостающие ![]() уравнений дает система уравнений ограничений (2):
уравнений дает система уравнений ограничений (2):
![]() ,
, ![]()
Итак, имеется система из ![]() уравнений для нахождения
уравнений для нахождения ![]() неизвестных:
неизвестных:
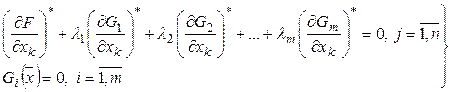 (11)
(11)
Полученный результат – система уравнений (11) составляет основное содержание ММЛ.
Легко понять, что систему уравнений (11) можно получить очень просто, вводя в рассмотрение специально сконструированную функцию Лагранжа (3).
Действительно
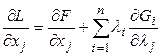 ,
, ![]() (12)
(12)
![]() ,
, ![]() (13)
(13)
Итак, система уравнений (11) представима в виде (используя (12), (13)):
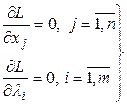 (14)
(14)
Система уравнений (14) представляет необходимое условие в классической задаче условной оптимизации.
Найденное в результате решение этой системы значение вектора ![]() называется условно-стационарной точкой.
называется условно-стационарной точкой.
Для того, чтобы выяснить характер условно-стационарной точки ![]() необходимо воспользоваться достаточными условиями.
необходимо воспользоваться достаточными условиями.
5.3 Достаточные условия в классической задаче условной оптимизации. Алгоритм ММЛ
Эти условия позволяют выяснить, является ли условно-стационарная точка ![]() точкой локального условного минимума, или точкой локального условного максимума.
точкой локального условного минимума, или точкой локального условного максимума.
Относительно просто, подобно тому, как были получены достаточные условия в задаче на безусловный экстремум. Можно получить достаточные условия и в задаче классической условной оптимизации.
Результат этого исследования:
![]()
где ![]() - точка локального условного минимума.
- точка локального условного минимума.
![]()
где ![]() - точка локального условного максимума,
- точка локального условного максимума, ![]() - матрица Гессе с элементами
- матрица Гессе с элементами
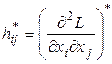 ,
, ![]()
Матрица Гессе ![]() имеет размерность
имеет размерность ![]() .
.
Размерность матрицы Гессе ![]() можно уменьшить, используя условие неравенства нулю якобиана:
можно уменьшить, используя условие неравенства нулю якобиана: ![]() . При этом условии можно зависимые переменные
. При этом условии можно зависимые переменные ![]() выразить через независимые переменные
выразить через независимые переменные ![]() , тогда матрица Гессе будет иметь размерность
, тогда матрица Гессе будет иметь размерность ![]() , т.е. необходимо говорить о матрице
, т.е. необходимо говорить о матрице ![]() с элементами
с элементами
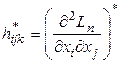 ,
, ![]()
тогда достаточные условия будут иметь вид:
![]() ,
, ![]() - точка локального условного минимума.
- точка локального условного минимума.
![]() ,
, ![]() - точка локального условного максимума.
- точка локального условного максимума.
Доказательство: Алгоритм ММЛ:
1) составляем функцию Лагранжа: ![]() ;
;
2) используя необходимые условия, формируем систему уравнений:
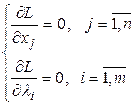
3) из решения этой системы находим точку ![]() ;
;
4) используя достаточные условия, определяем, является ли точка ![]() точкой локального условного минимума или максимума, затем находим
точкой локального условного минимума или максимума, затем находим
![]()
1.5.4. Графо-аналитический метод решения классической задачи условной оптимизации в пространстве ![]() и его модификации при решении простейших задач ИП и АП
и его модификации при решении простейших задач ИП и АП
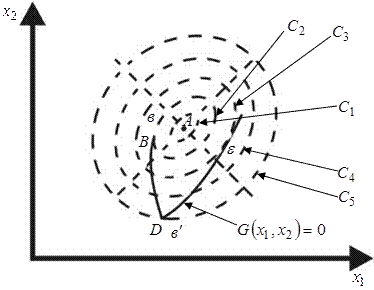
Этот метод использует геометрическую интерпретацию классической задачи условной оптимизации и основан на ряде важных фактов, присущих этой задаче.
![]() ;
; ![]() ;
; ![]() ;
;
![]()
![]()
В ![]() - общая касательная для функции
- общая касательная для функции ![]() и функции
и функции ![]() , представляющей ОДР
, представляющей ОДР ![]() .
.
Как видно из рисунка точка ![]() - точка безусловного минимума, точка
- точка безусловного минимума, точка ![]() точка условного локального минимума, точка
точка условного локального минимума, точка ![]() - точка условного локального максимума.
- точка условного локального максимума.
Докажем, что в точках условных локальных экстремумов кривая ![]() и соответствующие линии уровня
и соответствующие линии уровня
![]() ;
; ![]() .
.
Из курса МА известно, что в точке касания выполняется условие
![]()
где ![]() - угловой коэффициент касательной, проведенной соответствующей линией уровня;
- угловой коэффициент касательной, проведенной соответствующей линией уровня; ![]() - угловой коэффициент касательной, проведенной к функции
- угловой коэффициент касательной, проведенной к функции
![]()
Известно выражение (МА) для этих коэффициентов:
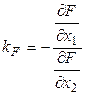 ;
; 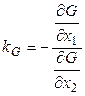
Докажем, что эти коэффициенты равны.
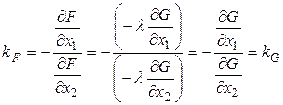
![]() ;
; ![]()
потому что об этом "говорят" необходимые условия
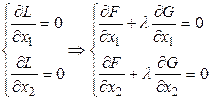
![]() .
.
Вышесказанное позволяет сформулировать алгоритм ГФА метода решения классической задачи условной оптимизации:
1) строим семейство линий уровня целевой функции:
![]() ;
; ![]() ;
;
2) строим ОДР, используя уравнение ограничения
![]()
3) с целью внесения исправления возрастания функции ![]() , находим
, находим ![]() и выясняем характер экстремальных точек;
и выясняем характер экстремальных точек;
4) исследуем взаимодействие линий уровня и функции ![]() , находя при этом из системы уравнений
, находя при этом из системы уравнений 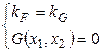 координаты условно стационарных точек – локальных условных минимумов и локальных условных максимумов.
координаты условно стационарных точек – локальных условных минимумов и локальных условных максимумов.
5) вычисляем
![]()
Следует особо отметить, что основные этапы ГФА метода решения классической задачи условной оптимизации совпадают с основными этапами ГФА метода решения задач НП и ЛП, отличие лишь в ОДР ![]() , а также в нахождении местоположения экстремальных точек в ОДР (например, в задачах ЛП эти точки обязательно находятся в вершинах выпуклого многоугольника, представляющего ОДР
, а также в нахождении местоположения экстремальных точек в ОДР (например, в задачах ЛП эти точки обязательно находятся в вершинах выпуклого многоугольника, представляющего ОДР ![]() ).
).
5.5. О практическом смысле ММЛ
Представим классическую задачу условной оптимизации в виде:
![]() (1)
(1)
![]() (2)
(2)
где ![]() - переменные величины, представляющие в прикладных технических и экономических задачах переменные ресурсы.
- переменные величины, представляющие в прикладных технических и экономических задачах переменные ресурсы.
В пространстве ![]() задача (1), (2) принимает вид:
задача (1), (2) принимает вид:
![]() (1')
(1')
![]()
где ![]() - переменная величина. (2')
- переменная величина. (2')
Пусть ![]() - точка условного экстремума:
- точка условного экстремума:
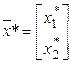
При изменении ![]() изменяется
изменяется
![]() , т.е.
, т.е. ![]()
Соответственно изменится и значение целевой функции:
![]()
Вычислим производную:
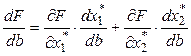 . (3)
. (3)
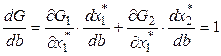 (4)
(4)
![]() (5)
(5)
Из (3), (4), (5)![]()
![]() . (6)
. (6)
Из (5)![]()
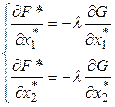 . (5')
. (5')
Подставим (5') в (3) и получаем:
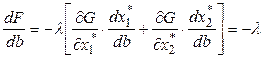 (6')
(6')
Из (6)![]() , что множитель Лагранжа
, что множитель Лагранжа ![]() характеризует "реакцию" значение
характеризует "реакцию" значение ![]() (ортогональна значению целевой функции) на изменения параметра
(ортогональна значению целевой функции) на изменения параметра ![]() .
.
В общем случае (6) принимает вид:
![]() ;
; ![]() (7)
(7)
Из (6), (7)![]() , что множитель
, что множитель ![]() ,
, ![]() характеризует изменение
характеризует изменение ![]() при изменении соответствующего
при изменении соответствующего ![]() -того ресурса на 1.
-того ресурса на 1.
Если ![]() - максимальная прибыль или минимальная стоимость, то
- максимальная прибыль или минимальная стоимость, то ![]() ,
, ![]() характеризует изменения этой величины при изменении
характеризует изменения этой величины при изменении ![]() ,
, ![]() на 1.
на 1.
5.6. Классическая задача условной оптимизации, как задача о нахождении седловой точки функции Лагранжа: ![]()
Пара ![]() называется седловой точкой, если выполняется неравенство.
называется седловой точкой, если выполняется неравенство.
![]() (1)
(1)
Очевидно, что из (1)![]()
![]() . (2)
. (2)
Из (2)![]() , что
, что 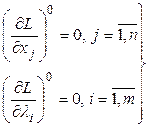 . (3)
. (3)
Как видно система (3) содержит ![]() уравнений, подобных тем
уравнений, подобных тем ![]() уравнениям, которые представляют необходимое условие в классической задаче условной оптимизации:
уравнениям, которые представляют необходимое условие в классической задаче условной оптимизации:
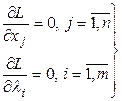 (4)
(4)
где ![]() - функция Лагранжа.
- функция Лагранжа.
В связи с аналогией систем уравнений (3) и (4), классическую задачу условной оптимизации можно рассматривать как задачу о нахождении седловой точки функции Лагранжа.
Похожие работы
-
Типовой расчет графов
Данная работа является типовым расчетом по курсу "Дискретная математика" по теме "Графы", предлагаемая студентам МГТУ им. Баумана.
-
Нелинейная теория функции Зильберта в частных производных
Министерство Образования и Науки Украины Харьковский национальный университет имени Н.Н. Зильберта А.А. Тензор, В.В. Невязкин Нелинейная теория функции Зильберта
-
Основные понятия и решения моделирования
Юридический техникум Рассмотрено и одобрено ПЦК г. Кропоткин программирования Председатель ПЦК Покалицына О.В. План чтения лекции по учебной дисциплине
-
Математическая модель распределения информации
Математическая модель распределения информации Математическая модель системы распределения информации включает следующие три основных элемента: входящий поток вызовов (требований на обслуживание), схему системы распределения информации, дисциплину обслуживания потока вызовов.
-
Сравнительный анализ методов оптимизации
Математическая задача оптимизации. Минимум функции одной и многих переменных. Унимодальные и выпуклые функции. Прямые методы безусловной оптимизации и минимизации, их практическое применение. Методы деления отрезка пополам (дихотомия) и золотого сечения.
-
Методы спуска
Решение задач безусловной минимизации методами спуска: метод градиентного и покоординатного спуска.
-
Экзаменационные билеты по методам оптимизации за весенний семестр 2001 года
примерный перечень экзаменационных вопросов методы оптимизации Сформулируйте понятие «оптимизации». Приведите примеры сфер деятельности, где можно использовать методы оптимизации.
-
Модели и методы принятия решений
Нахождение экстремумов функций методом множителей Лагранжа. Выражение расширенной целевой функции. Схема алгоритма численного решения задачи методом штрафных функций в сочетании с методом безусловной минимизации. Построение линий ограничений.
-
Поиск оптимальных решений
Основные понятия оптимизационных задач. Нахождение наибольших или наименьших значений многомерных функций в заданной области. Итерационные процессы с учетом градиента. Функционал для градиентного равенства и применение его в задачах условной оптимизации.
-
Сравнительный анализ методов оптимизации
Оптимизация как раздел математики, ее определение, сущность, цели, формулировка и особенности постановки задач. Общая характеристика различных методов математической оптимизации функции. Листинг программ основных методов решения задач оптимизации функции.