Название: Побудова скінченних множин
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 50.06 Kb
Скачать файл: referat.me-215172.docx
Краткое описание работы: Множина як визначена сукупність елементів чи об’єктів. Списковий спосіб подання множини. Множина, кількість елементів якої скінченна (скінченна множина). Виведення декартового добутку з кожної заданої комбінації. Алгоритм рішення та реалізація програми.
Побудова скінченних множин
Міністерство освіти і науки України
Полтавський національний технічний університет
імені Юрія Кондратюка
Факультет інформаційних та телекомунікаційних технологій і систем
Кафедра комп’ютерних та інформаційних технологій і систем
Розрахунково-графічна робота
з дисциплін "Основи дискретної математики"
та "Основи програмування та алгоритмічні мови"
Виконав:
Студент групи 101-ТН
Селін Ігор
Керівник:
д.т.н. Ляхов Олександр Логвинович
![]() Полтава 2010
Полтава 2010
Постановка задачі
УМОВА ЗАДАЧІ:
Дано скінчені множини А, В, С. Побудувати множини ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Множина - це деяка визначена сукупність елементів чи об’єктів.
Списковий спосіб подання множини - перелік усіх елементів у фігурних дужках.
Прямим (або декартовим) добутком множини А і Б називають множину всіх упорядкованих пар елементів (а, б), з яких перший належить множині А, а другий - множині Б.
Скінченна множина - множина, кількість елементів якої скінченна, тобто існує натуральне числоk , що є числом елементів цієї множини.
Розв’ язання задачі.
Маємо три множини - A,B,C. Кожна з них містить по 5 елементів. Для наглядного представлення покажемо приклад декартового добутку, в якому взято три двохелементні множини з випадковими елементами:
A={0,1}
B={1,1}
C={0,0}
AxBxC={a1,b1,c1},{a2,b1,c1},{a1,b1,c2},{a1,b2,c1},{a1,b2,c2},{a2,b2,c2}=
={0,1,0},{1,1,0},{0,1,0},{0,1,0},{0,1,0}{1,1,0}
Алгоритм задачі.
Для винання цієї задачі, ми взяли вхідні дані, що являють собою три множини по 5 елементів.
Так як декартовий добуток являє собою пари елементів із кожної множини, на потрібно перерахувати ці пари. В нашому випадку трійки значень. Для цьго використаємо 3 цикли, кожен яких буде перелічувати множину. Комбінації множин я змінив до вказаних в умові. За один прохід кожного цикла виводиться 1 добуток з кожної заданої комбінації.
Реалізація програми
#include <iostream>
using namespace std;
int a [10] ={1,1,1,0,0};
int b [10] ={0,0,1,0,1};
int c [10] ={1,0,1,1,0};
int abc [10] [6] ;
int main ()
{
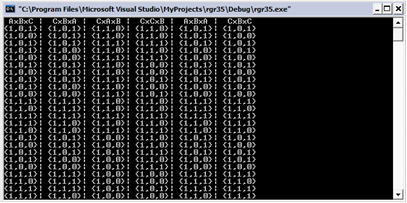
cout<<" AxBxC "<<"| CxBxA "<<"| CxAxB "<<"| CxCxB "<<"| AxBxA "<<"| CxBxC "<< endl;
for (int x=0; x<5; x++)
for (int y=0; y<5; y++)
for (int z=0; z<5; z++)
{
cout<<"{"<<a [x] <<","<<b [y] <<","<<c [z] <<"}";
cout<<"| {"<<c [x] <<","<<b [y] <<","<<a [z] <<"}";
cout<<"| {"<<c [x] <<","<<a [y] <<","<<b [z] <<"}";
cout<<"| {"<<c [x] <<","<<c [y] <<","<<b [z] <<"}";
cout<<"| {"<<a [x] <<","<<b [y] <<","<<a [z] <<"}";
cout<<"| {"<<c [x] <<","<<b [y] <<","<<c [z] <<"}"<<endl;
}
cout<<endl;
cin. get ();
cin. get ();
return 0;
}
Початкові дані:
A={1,1,1,0,0}
B={0,0,1,0,1}
C={1,0,1,1,0}
Демонстрац ія програми:
Похожие работы
-
Алгебра 10 класс Мерзляк профиль
А. Г. Мерзляк Д. А. Номіровський В. Б. Полонський М. С. Якір АЛГЕБРА Підручник для класу загальноосвітніх навчальних закладів Профільний рівень Рекомендовано
-
Алгебра 10 класс Мерзляк академ
А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір АлгебрА і почАтки АнАлізу Підручник для загальноосвітніх навчальних закладів Академічний рівень
-
Теорія споживання
Контрольна робота з теми: ТЕОРІЯ СПОЖИВАННЯ Вступ Математичні моделі й методи, що досліджуються в даній роботі, є необхідними для вивчення споживчого поводження на ринку готової продукції, переваг індивідуального споживача, корисності й класифікації товарів, еластичності й інших властивостей попиту.
-
Вивчення поняття відносин залежності
Курсова робота Вивчення поняття відносин залежності Зміст Введення 1. Визначення й приклади 2. Простір залежності 3. Транзитивність 4. Зв'язок транзитивних відносин залежності з операторами замикання
-
Дослідження топологічного визначення верхніх напівґрат
Визначення та властивості упорядкованих множин, приклади діаграм. Дистрибутивні ґрати як один з основних алгебраїчних об'єктів. Поняття нижньої і точної грані, їх властивості та приклади, доказ лем. Застосування та суть топологічних стоунових просторів.
-
Дослідження лінійно впорядкованого простору ординальних чисел
Джерела теорії впорядкованих і частково впорядкованих алгебраїчних систем. Лінійно впорядкований простір ординальних чисел. Цілком упорядковані множини і їхні властивості. Кінцеві ланцюги і їхні порядкові типи. Загальні властивості ординальних чисел.
-
Наведення усіх перестановок елементів множини
Перестановка як перевпорядкованість наборів елементів, об’єктів або функція, що задає таку перевпорядкованість. Всі можливі варіанти перестановок елементів множини за умови наявності трьох елементів за умови, що жоден елемент не залишається на місці.
-
Числення висловлень
Реферат на тему: Числення висловлень Числення висловлень ) згідно з поданою у розділі 1 схемою означається таким чином. Алфавіт числення висловлень складається з елементарних і змінних висловлень (пропозиційних змінних): a,b,c,d,...,x,y,z (можливо з індексами), знаків логічних операцій ,,, і круглих дужок ( та ).
-
Знаходження кусково-постійних конфігурацій множин
Основні засади комбінаторики та теорії множин на основі аксіоматики Цермело-Френкеля і використання правила суми й добутку. Знаходження кусково-постійних конфігурацій множин засобами мови програмування IDE C++ Builder з допомогою вбудованого GUI.
-
Прикладне вживання методів дискретної математики
МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота Прикладне вживання методів дискретної математики м. Бердичів 2007 р.