Название: Прикладне вживання методів дискретної математики

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 59.46 Kb

Скачать файл: referat.me-215102.docx

Краткое описание работы: МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ Бердичівський політехнічний коледж Контрольна робота Прикладне вживання методів дискретної математики м. Бердичів 2007 р.

Прикладне вживання методів дискретної математики

МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ

Бердичівський політехнічний коледж

Контрольна робота

Прикладне вживання методів дискретної математики

м.Бердичів 2007 р.

Зміст

Задача 1

Задача 2

Задача 3

Задача 4

Список використаної літератури

1. Задача 1

1. Задана універсальна множина U={a,b,c,d,e,f,g,h,i} і дві множини S={b,c,e,i}, T={c,e,f,i}. Знайти:

a) об’єднання, перетин, різницю і симетричну різницю множин SiT;

b) доповнення множини Sі доповнення множини T;

c) прямий добуток множин SiT;

d) задати функцію із Sв T: ін’єктивну, сюр’єктивну і бієктивну.

2. Дані відображення h¹ і h² , що представляють множину сумісних кортежів. Знайти:

a) h³ =(h¹ Èh² );

b) h⁴ =(h¹ Çh² );

c) h⁵ =(h¹ h² );

h1	у	x1	x2	x 3	h2	у	x1	x2	x 3
2	b	e	6	3	с	e	6
3	с	e	5	5	с	b	2
5	с	b	2	4	а	c	5
4	а	e	5	2	b	e	6

d) h⁶ =(h¹ Dh² ).

3. Хай дані відношення r¹ і r² . Знайти:

a) r³ =(r¹ Èr² );

b) r⁴ =(r¹ Çr² );

c) r⁵ =(r¹ r² ).

d) r⁶ =(r¹ Dr² ).

r1	x1	x2	x3	x4	r2	x1	x2	x3	x4
x1	1	1	0	1	x1	1	1	0	1
x2	0	1	0	1	x2	1	1	0	0
x3	1	0	1	0	x3	0	1	0	0
x4	0	1	1	1	x4	0	0	1	1

Відповідь:

1.

а)А=SÈT = {b, c, e, f, i};

А= SÇT = {c, e, i};

A = ST = {b}; B = TS = {f}:

A = SDT = {b, f}.

b) A = ùS = {a, d, f, g, h};

B = ùT = {a, b, d, g, h}.

c) SÄT= {{b, c}, {b, e}, {b, f}, {b, i}, {c, c}, {c, e}, {c, f}, {c, i}, {e, c}, {e, e}, {e, f}, {e, i}, {i, c}, {i, e}, {i, f}, {i, i}}.

2.

a) h³ =

у	x1	x2	x 3
2	b	e	6
3	с	e	5
5	с	b	2
4	а	e	5
3	с	e	6
4	а	c	5

b) h⁴ =

c) h⁵ =

у	x1	x2	x 3
3	с	e	5
4	а	e	5

d) h⁶ =

у x1 x2 x 3 2 b e 6 5 с b 2

3.

a)

r 3	x1	x2	x3	x4
x1	1	1	0	1
x2	1	1	0	1
x3	1	1	1	0
x4	0	1	1	1

b)

r 4	x1	x2	x3	x4
x1	1	1	0	1
x2	0	1	0	0
x3	0	0	0	0
x4	0	0	1	1

c)

r 3	x1	x2	x3	x4
x1	0	0	0	0
x2	0	0	0	1
x3	1	0	1	0
x4	0	1	0	0

d)

r 3	x1	x2	x3	x4
x1	0	0	0	0
x2	1	0	0	1
x3	1	1	1	0
x4	0	1	0	0

2. Задача 2

У колоді 52 карти. У скількох випадках при виборі з колоди 10 карт серед них виявляться: а) рівно один туз; б) хоча б один туз; в) не менше двох тузів; г) рівно два тузи?

Відповідь:

а) Всього у колоді 4 тузи. Отже за правилом добутку перемножимо ймовірність вибору з чотирьох тузів одного туза та ймовірність вибору інших карт, тобто 9 з 48:

.

б) Хоча б один туз – це означає може бути і 4, і 3, і 2, і 1. Отже для розв'язку необхідно від ймовірності вибору 10 карт з 52 відняти ймовірність вибору 10 карт з 48:

.

в) Не менше двох тузів – означає, що з 10 карт буде 4, 3 або 2 тузи. Рішенням буде попередня відповідь від якої відняти ймовірність вибору 1 туза (першої відповіді):

.

г) Аналогічно розв'язку першого завдання отримаєм:

3. Задача 3

Граф заданий матрицею вагів. Побудувати для нього остов мінімальної ваги використовуючи алгоритми Пріма та Краскала, за алгоритмом Флойда обчислити найкоротші шляхи графа.

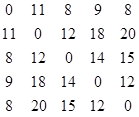
Відповідь:

Будова графа:

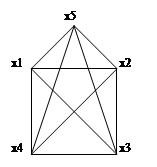
Побудова остову мінімальної ваги по алгоритму Краскала:

Встановлюємо частковий порядок по вазі ребер графа:

L13	L15	L14	L12	L23	L45	L34	L35	L24	L25
8	8	9	11	12	12	14	15	18	20

Будуємо остов мінімальної ваги:

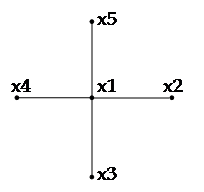
Крок	Ребра остову				Вершини остову
	L13	L15	L14	L12	x1	x2	x3	x4	x5
1	1	0	0	0	1	1	0	0	0
2	1	1	0	0	1	1	1	0	0
3	1	1	1	0	1	1	1	1	0
4	1	1	1	1	1	1	1	1	1
Lij	8	8	9	11	L=8+8+9+11=36

Обчислення найкоротших шляхів за алгоритмом Флойда:

Будуємо матрицю вагів та матрицю переходів:

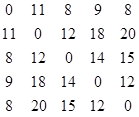А₀ = Р₀ =

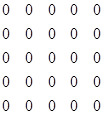
Елементи матриці вагів будемо знаходити за формулою:

A_k [i; j] = min (A_k-1 [i; j], A_k-1 [i; k] + A_k-1 [k; j])

Перша ітерація:k=1

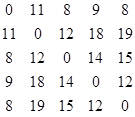А₁ = Р₁ =

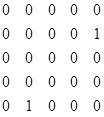
Друга ітерація:k=2

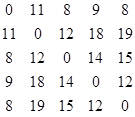А₂ = Р₂ =

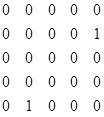
Третя ітерація:k=3

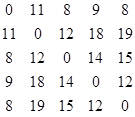А₃ = Р₃ =

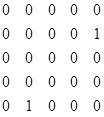
Четверта ітерація:k=4

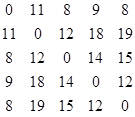А₄ = Р₄ =

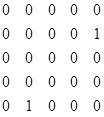
П’ята ітерація:k=5

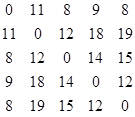А₅ = Р₅ =

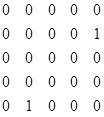
4. Задача 4

Знайти мінімальну ДНФ логічної функції F= F(х_г , х₂ , х₃ , х₄ ), яка дорівнює одиниці на наборах 2, 3, 4, 11, 14, 15 і нулю на решті наборів.

Відповідь:

Спочатку необхідно подати функцію у ДДНФ.

ДДНФ =x₁ x₂ x₃ x₄ Úx₁ x₂ x₃ x₄ Úx₁ x₂ x₃ x₄ Úx₁ x₂ x₃ x₄ Úx₁ x₂ x₃ x₄ Úx₁ x₂ x₃ x₄

Виконуємо склеювання:

1-2 x₁ x₂ x₃

1-4 x₂ x₃ x₄

2-4 x₂ x₃ x₄

4-6 x₁ x₃ x₄

5-6 x₁ x₂ x₃

ДДНФ = x₁ x₂ x₃ Úx₂ x₃ x₄ Úx₂ x₃ x₄ Úx₁ x₃ x₄ Úx₁ x₂ x₃ Úx₁ x₂ x₃ x₄

1-2 x₂ x₃

1-3 x₂ x₃

2-3 x₂ x₃

3-4 x₃ x₄

4-5 x₁ x₃

ДДНФ = x₂ x₃ Úx₃ x₄ Úx₁ x₃ Úx₁ x₂ x₃ x₄

ДДНФ	x1 x2 x3 x4	x1 x2 x3 x4	x1 x2 x3 x4	x1 x2 x3 x4	x1 x2 x3 x4	x1 x2 x3 x4
x2 x3	+	+	-	+	-	-
x3 x4	-	+	-	+	-	+
x1 x3	-	-	-	+	+	+
x1 x2 x3 x4	-	-	+	-	-	-

Отже,

minДНФ = x₁ x₃ Úx₂ x₃ Úx₁ x₂ x₃ x₄

Список використаної літератури

1. «Дискретна математика» С.Лук’яненко. К-2000

2. «Комбінаторика» Д.Сафонов. М-1992

3. «Комбінаторика для програмістів» В.Липський. М-1988

4. Конспект лекцій

5. Комп’ютерна мережа Інтернет