Название: Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.17
Вид работы: реферат
Рубрика: Математика
Размер файла: 63.15 Kb
Скачать файл: referat.me-215481.docx
Краткое описание работы: Задача 17 . Найти производную -го порядка. 17.1. y'= eαx+αxeαx y''= 2αeαx+α2xeαx y'''= 3α2eαx+α3xeαx
Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.17
Задача 17
. Найти производную ![]() -го порядка.
-го порядка.
17.1. ![]()
y'= eαx +αxeαx
y''= 2αeαx +α2 xeαx
y'''= 3α2 eαx +α3 xeαx
y( n ) = nαn -1 eαx +αn xeαx
17.2. ![]()
y'= 2cos2x-sin(x+1)
y''= -4sin2x-cos(x+1)
y'''= -8cos2x+sin(x+1)
y(n) = 2n sin(π/2+2x)+cos(π/2+x+1)
17.3. ![]()
y'= 7/5*5 √e7 x -1
y''= 49/25*5 √e7 x -1
y'''= 343/125*5 √e7 x -1
y( n ) = (7/5)n *5 √e7 x -1
17.4. 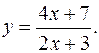
y'= -2/(2x+3)2
y''= 8/(2x+3)3
y'''= -48/(2x+3)4
y(n) = (-1)n 2n n!/(2x+3)n+1
17.5. ![]()
y'= 5lge
5x+2
y''= -25lge
(5x+2)2
y'''= 250lge
(5x+2)3
y(n) = (-1)n+1 5n (n-1)!lge , n≠1
(5x+2)n
17.6. ![]()
y'= 3lna*a3x
y''= 32 ln2 a*a3x
y'''= 33 ln3 a*a3x
y(n) = 3n lnn a*a3x
17.7. 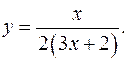
y'= 1/(3x+2)2
y''= -2/(3x+2)3
y'''= 54/(3x+2)4
y(n) = (-1)n+1 3n-1 n!
(3x+2)n+1
17.8. ![]()
y'= lge
x+4
y''= -lge_
(x+4)2
y'''= 2lge
(x+4)3
y(n) = (-1)n+1 (n-1)!lge , n≠1
(x+4)n
17.9. ![]()
y'= 1/(2√x)
y''= -1/(4√x)
y'''= 1/(8√x)
y(n) = 1/(2n √x)
17.10. 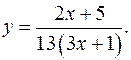
y'= 1/(3x+1)2
y''= -6/(3x+1)3
y'''= 54/(3x+1)4
y(n) = (-1)n+1 3n-1 n!/(3x+1)n+1
17.11. ![]()
y'= 3ln2*33x+5
y''= 32 ln2 2*33x+5
y'''= 33 ln3 2*33x+5
y(n) = 3n lnn 2*33x+5
17.12. ![]()
y'= cos(x+1)-2sin2x
y''= -sin(x+1)-4cos2x
y'''= -cos(x+1)+8sin2x
y(n) = sin(π/2+x+1)+2n cos(π/2+2x)
17.13. ![]()
y'= 2/3*3 √e2 x+ 1
y''= 4/9*3 √e2 x+ 1
y'''= 16/81*3 √e2 x+ 1
y(n) = (2/3)n *3 √e2 x +1
17.14. 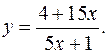
y'= -5/(5x+1)2
y''= 50/(5x+1)3
y'''= -750/(5x+1)4
y(n) = (-1)n+1 5n n!/(5x+1)n+1
17.15. ![]()
y'= 3lge
3x+1
y''= -9lge
(3x+1)2
y'''= 54lge
(3x+1)3
y(n) = (-1)n+1 3n (n-1)!lge , n≠1
(3x+1)n
17.16. ![]()
y'= 5ln5*75x
y''= 52 ln2 5*75x
y'''= 53 ln3 5*75x
y(n) = 5n lnn 5*75x
17.17. 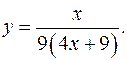
y'= 1/(4x+9)2
y''= -8/(4x+9)3
y'''= 96/(4x+9)4
y(n) = (-1)n+1 4n-1 n!/(4x+9)n+1
17.18. ![]()
y'= lge
x+1
y''= -lge_
(x+1)2
y'''= 2lge
(x+1)3
y(n) = (-1)n+1 (n-1)!lge , n≠1
(x+1)n
17.19. 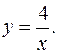
y'= -4/x2
y''= 8/x3
y'''= -24/x4
y(n) = (-1)n 4n!/xn-1
17.20. 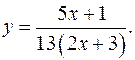
y'= 1/(2x+3)2
y''= -4/(2x+3)3
y'''= 24/(2x+3)4
y(n) = (-1)n+1 2n-1 n!/(2x+3)n+1
17.21. ![]()
y'= 2lna*a2x+3
y''= 22 ln2 a*a2x+3
y'''= 23 ln3 a*a2x+3
y(n) = 2n lnn a*a2x+3
17.22. ![]()
y'= 3cos(3x+1)-5sin5x
y''= -9sin(3x+1)-25cos5x
y'''= -27cos(3x+1)+125sin5x
y(n) = 3n sin(π/2+3x+1)+5n cos(π/2+5x)
17.23. ![]()
y'= 3/2*√e3x+1
y''= (3/2)2 *√e3x+1
y'''= (3/2)3 *√e3x+1
y(n) = (3/2)n *√e3x+1
17.24. 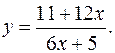
y'= -6/(6x+5)2
y''= 36/(6x+5)3
y'''= 216/(6x+5)4
y(n) = (-1)n 6n /(6x+5)n+1
17.25. ![]()
y'= 2lge
2x+7
y''= -4lge
(2x+7)2
y'''= 16lge
(2x+7)3
y(n) = (-1)n+1 2n (n-1)!lge , n≠1
(2x+7)n
17.26. ![]()
y'= kln2*2kx
y''= k2 ln2 2*2kx
y'''= k3 ln3 2*2kx
y(n) = kn lnn 2*2kx
17.27. 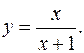
y'= 1/(x+1)2
y''= -2/(x+1)3
y'''= 6/(x+1)4
y(n) = (-1)n+1 n!/(x+1)n+1
17.28. ![]()
y'= 1/((x+5)ln3)
y''= -1/(x+5)2
y'''= 2/(x+5)3
y(n) = (-1)n+1 (n-1)!/(x+5)n
17.29. 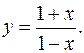
y'= 2/(1-x)2
y''= -4/(1-x)3
y'''= 12/(1-x)4
y(n) = (-1)n+1 2!/(1-x)n+1
17.30. 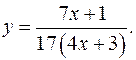
y'= 1/(4x+3)2
y''= -2/(4x+3)3
y'''= 6/(4x+3)4
y(n) = (-1)n+1 n!/(4x+3)n+1
17.31. ![]()
y'= 2ln3*32x+5
y''= 22 ln2 3*32x+5
y'''= 23 ln3 3*32x+5
y(n) = 2n lnn 3*32x+5
Похожие работы
-
Точечные и интервальные оценки
Уровень значимости α. Уровень значимости обычно обозначают греческой буквой (альфа). Статистическая значимость результата представляет собой меру уверенности в его истинности (в смысле репрезентативности выборки). Более точно, уровень значимости α - это показатель, обратно пропорциональный надежности результата.
-
Формулы тригонометрии
tg(α+β)=(tgα+tgβ)/(1–tgα·tgβ); tg(α-β)=(tgα–tgβ)/(1+tgα·tgβ) ctg(α+β)=(ctgα·ctgβ–1)/(ctgβ+ctgα); ctg(α+β)=(ctgα·ctgβ+1)/(ctgβ–ctgα)
-
Формулы и шпоры 10-11 кл. (информатика, геометрия, тригонометрия ...) (Шпаргалка)
Отрицание (инверсия) Конъюнкция (логическое произведение) АВ; А and В; А и В Дизъюнкция (логическое сложение, не исключающее или) А или В; А or В Дизъюнкзия (исключающий или, неравнозначность)
-
Способы решения систем линейных уравнений
– очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики, но недостаточно широко. А для того, чтобы перейти к исследованию данной темы, также нужно было познакомиться с темой матриц и определителей. Этот же материал вообще в школьной программе не изучается.
-
Геометрия чисел
Введение. Возникновением теории чисел мы, по большому счёту, обязаны Минковскому. Минковский (Minkowski), Герман - выдающийся математик (1864 - 1909), еврей, родом из России. Был профессором в Бонне, Кенигсберге, Цюрихе и Геттингене. Сблизил теорию чисел с геометрией, создав особое учение о "геометрии чисел" ("Geometrie der Zahlen", 1896 - 1910; "Diophantische Approzimationen", 1907, и др.).
-
Аксиоматика теории множеств
Содержание стр. Введение………………………………………………………………………….3 §1. Система аксиом…………………………………………………………….....4 Аксиома объемности…………………………………………………6
-
Метод золотого перерізу для пошуку екстремумів функцій
Розгляд нових методів екстримізації однієї змінної. Типи задач, які існують для розв’язування задач мінімізації на множині Х. Золотий поділ відрізка на дві неоднакові частини, дослідження його на стійкість. Алгоритм, текст програми, результат роботи.
-
Еволюційні рівняння з псевдо-Бесселевими операторами
Розвиток теорії задачi Кошi та двоточкової задачi для еволюцiйних рiвнянь з псевдо-Бесселевими операторами в класах початкових умов, що є узагальненими. Вивчення властивостей перетворення Бесселя функції та оператора узагальненого зсуву аргументу.
-
Решения к Сборнику заданий по высшей математике Кузнецова Л.А. - 2. Дифференцирование. Зад.19
Задача 19 . Найти производную второго порядка от функции, заданной параметрически. 19.1. x'= -2sin2t= -4sintcost y'= 4sint/cos3t y''xx= 4sint = -1 _ 16sin2tcos5t 4sintcos5t
-
Линейное и нелинейное программирование
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Севастопольский национальный технический университет Кафедра кибернетики и вычислительной техники Пояснительная записка