Название: Математика Древнего Египта

Вид работы: реферат

Рубрика: Математика

Размер файла: 27.61 Kb

Скачать файл: referat.me-215687.docx

Краткое описание работы: Достижения древнеегипетской математики. Источники, по которым можно судить об уровне знаний древних египтян. Задачи на арифметическую и геометрическую прогрессии, нахождение числа Пи, подчёркивают практический и теоретический характер древней математики.

Математика Древнего Египта

МАТЕМАТИКА ДРЕВНЕГО ЕГИПТА

Бурдун Вячеслав

г. Луганск

ССФМШ №1 6-а класс

11 лет

Математика Древнего Египта

Мы начнем наше исследование гораздо раньше указанных дат в описании проекта. Ведь успехи античных математиков (в том числе и Фалеса) не могли возникнуть на пустом месте. Народы Древнего востока на протяжении многих веков сделали немало открытий в арифметике, геометрии и астрономии.

Самые ранние математические тексты, известные в наши дни, оставили две великие цивилизации древности - Египет и Месопотамия. Именно там появились первые математические задачи, решения которых требовала повседневная жизнь.

Уровень древнеегипетской математики был довольно высок. Источников, по которым можно судить об уровне математических знаний древних египтян, совсем немного. Во-первых, это папирус Райнда, названный так по имени своего первого владельца. Он был найден в 1858 г., расшифрован и издан в 1870 г. Рукопись представляла собой узкую (33 см) и длинную (5,25 м) полосу папируса, содержащую 84 задачи. Теперь одна часть папируса хранится в Британском музее в Лондоне, а другая находится в Нью-Йорке. Во-вторых, так называемый Московский папирус - его в декабре 1888 г. приобрёл в Луксоре русский Египтолог Владимир Семёнович Голенищев. Сейчас папирус принадлежит Государственному музею изобразительных искусств имени А. С. Пушкина. Этот свиток длиной 5,44 м и шириной 8 см включает 25 задач. И наконец, "Кожаный свиток египетской математики", с большим трудом расправлённый в 1927 г. и во многом проливший свет на арифметические знания египтян. Ныне он хранится в Британском музее. Подобные папирусы, по-видимому, служили своего рода учебниками. В папирусах есть задачи на вычисление - образцы выполнения арифметических операций, задачи на раздел имущества, на нахождение объёма амбара или корзины, площади поля и т. д.

Все правила счёта древних египтян основывались на умении складывать и вычитать, удваивать числа и дополнять дроби до единицы. Умножение и деление сводили к сложению при помощи особой операции - многократного удвоения или раздвоения чисел. Выглядели такие расчёты довольно громоздко. Для дробей были специальные обозначения. Египтяне использовали дроби вида 1/n, где n - натуральное число. Такие дроби называются аликвотными. Иногда вместо деления m:n производили умножение m*(1/n). Надо сказать, что действия с дробями составляли особенность египетской арифметики, в которой самые простые вычисления порой превращались в сложные задачи.

Сравнительно небольшой круг задач в египетских папирусах сводится к решению простейших уравнений с одним неизвестным. При решении подобных задач для неизвестного использовали специальный иероглиф со значением "куча". В задачах про "кучу", решаемых единым методом, можно усмотреть зачатки алгебры как науки об уравнениях.

В египетских папирусах встречаются также задачи на арифметическую и геометрическую прогрессии, что ещё раз подчёркивает не только практический, но и теоретический характер древней математики. Поразительно, но при довольно примитивной и громоздкой арифметике египтяне смогли добиться значительных успехов в геометрии. Они умели точно находить площадь поля прямоугольной, треугольной и трапециевидной формы. Известно, что в середине І тысячелетия до н. э. для построения прямого угла египтяне использовали верёвку, разделённую узлами на 12 равных частей. Концы верёвки связывали и затем натягивали её на 3 колышка. Если стороны относились как 3:4:5, то получался прямоугольный треугольник. И это - единственный прямоугольный треугольник, который знали в Древнем Египте.

Важным достижением геометрической науки египтян было очень хорошее приближение числа π, которое получается из формулы для площади круга диаметра d. Этому правилу из 50-ой задачи папируса Райанда соответствует значение π» 3,1605. Однако каким образом египтяне получили саму формулу, из контекста неясно. Заметим, что на всём Древнем Востоке при вычислениях использовалось значение π=3. Так что в этом отношении египтяне намного опередили другие народы.

Среди пространственных тел самым "египетским" можно считать пирамиду, ведь именно такую форму имеют знаменитые усыпальницы фараонов. Так вот, оказывается, кроме объёма куба, параллелепипеда, призмы и цилиндра египтяне умели вычислять объём усечённой пирамиды, в основаниях которой лежат квадраты со сторонами a и b, а высота h. Для этого они применяли специальную формулу. Эта формула считается высшим достижением древнеегипетской математики.

Математика в Древнем Египте представляла собой совокупность знаний, между которыми ещё не существовало чётких границ. Это были правила для решения конкретных задач, имевших практическое значение. И лишь постепенно, очень и очень медленно, задачи начали обобщаться и приобретать более абстрактные черты.

Как могло появиться первое приближение числа π

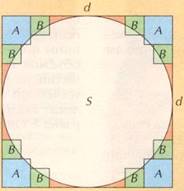
По поводу формулы площади круга нам кажется весьма правдоподобной гипотеза автора многочисленных книг по истории математика А.Е. Раик: площадь круга диаметра d сравнивается с площадью описанного вокруг него квадрата, из которого по очереди удаляются малые квадраты со сторонами (1/6)d и (1/9)d.

В наших обозначениях вычисления будут выглядеть так. В первом приближении площади круга S равна разности между площадью квадрата со стороной d и суммарной площадью 4-ёх малых квадратов А со стороной (1/6)d:

S » d² -4(1/6*d)² =d² (1-1/9)=(8/9)d²

Далее из полученной площади нужно вычесть площадь 8-ми квадратов В со стороной (1/9)d, и тогда площадь круга будет приближённо равна следующему выражению:

S » (1-1/9)d² -8(1/9*d)² =(1-1/9)d² -1/9*(8/9)d² =(1-1/9)d² -1/9(1-1/9)d² =(1-1/9)² d²