Название: Функции и их производные

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 68.77 Kb

Скачать файл: referat.me-215738.docx

Краткое описание работы: Правило нахождения производной произведения функций. Формулы нахождения производных для функций, заданных параметрически. Геометрический смысл производной. Приращение и дифференциал функции. Наибольшее и наименьшее значения на замкнутом множестве.

Функции и их производные

КОНТРОЛЬНАЯ РАБОТА № 4

ВАРИАНТ 4.3

№ 1.

а) Найти производные от данных функций:

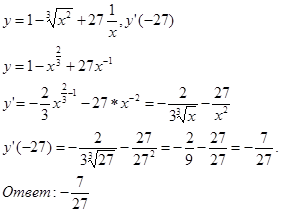
б)

Применяем правило нахождения производной произведения функций

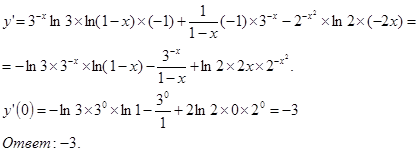
в)

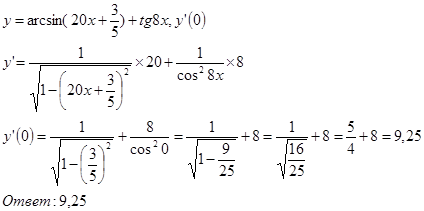
№ 2

Дана функция

Найти:

а) координаты вектора gradu в точке А (-1,3,2)

По определению:

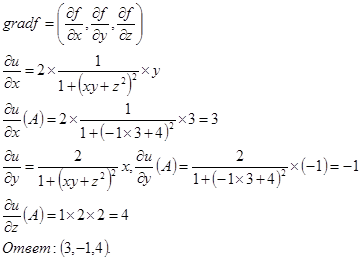
б) в точке А в направлении вектора а{2,-6,-3}

По определению:

Величины найдены в п.а)

Найдем cosб, cosв, cosг.

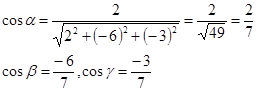
По формуле получаем:

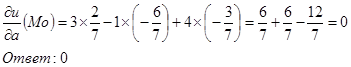
№ 3.

Дана функция .

Найти y”. Вычислить y”(-1).

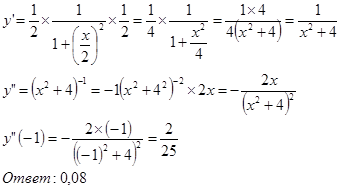
№ 4.

Доказать, что функция удовлетворяет уравнению

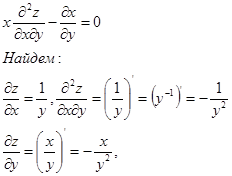
подставляем найденные выражения в уравнение, получаем: , что и требовалось доказать.

№5

Найти если

Вычислить если .

Воспользуемся формулами нахождения производных для функций, заданных параметрически

№ 6.

Функции задана неявно уравнением

Вычислить:

а)

Вычисления проводим по формуле

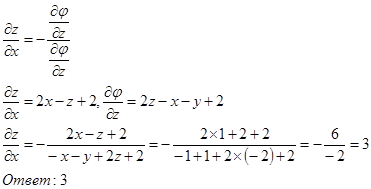
б)

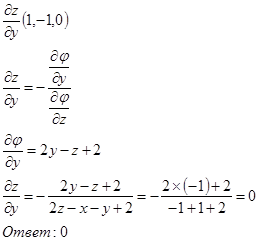
№ 7.

На графике функции y=ln2x взята точка А. Касательная к графику в точке А наклонена к оси ОХ под углом, тангенс которого равен ј. Найти абсциссу точки А.

Из геометрического смысла производной имеем

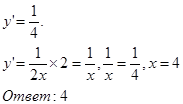
№ 8.

Найти dy, если у=х⁶ . Вычислить значение dy, если

Для имеем

№ 9.

Дана функция и точки и

Вычислить Дz и dz при переходе из точки М₀ в точку М₁ . Приращение функции Дz равно

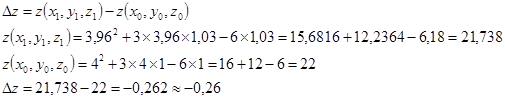
Дифференциал функции dz равен

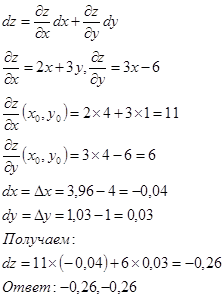
№ 10.

Дана функция . Найти ее наибольшее и наименьшее значения на отрезке [0;6]. Найдем

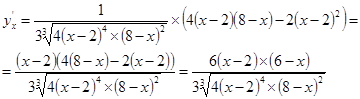
Приравниваем числитель к нулю при условии

Решение отбрасываем.

совпадает с граничным значением.

Найдем значение функции в точках x=0 и x=6.

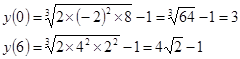
Наибольшее значение функции на отрезке [0;6] равно , наименьшее равно 3.

№ 11

Дана функция .

Найти ее наибольшее и наименьшее значения на замкнутом множестве, ограниченном прямыми .

Найдем стационарные точки из системы уравнений

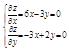
Решаем систему уравнений

Сделаем чертеж

На участке границы х=-1 функция z(х,у) превращается в функцию одной переменной

Найдем наибольшее и наименьшее значение этой функции на обрезке [-1;2]. Имеем , отсюда . Это значение не принадлежит отрезку [-1;2]. Z(-1)=5. Z(2)=4+6+7=17.

На участке у=-1 получаем

Найдем наибольшее и наименьшее значение этой функции на отрезке [-1;2]. Имеем , отсюда .

Находим

На участке границы у=1-х получаем функцию

Найдем наибольшее и наименьшее значение этой функции на участке [-1;2].

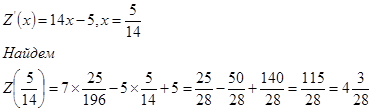
На границах отрезка

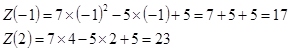
Сравниваем все найденные значения функции

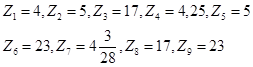
видим, что наибольшее значение достигается в точке (2;-1) и равно 23, а наименьшее равно 4 и достигается в точке (0;0).

Ответ: 23;4.

№ 12.

Провести полное исследование функции и начертить ее график.

1. Найдем область определения функции .

Функция непериодична.

2. Установим наличие симметрии относительно оси OY или начала координат по четности или нечетности функции , симметрии нет.

3. Определим «поведение функции в бесконечности»

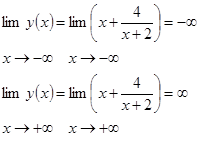
4. Точка разрыва х=-2

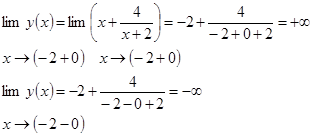
5. найдем пересечение кривой с осями координат

т.А (0;2)

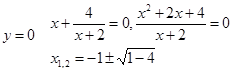
Корней нет, нет пересечения с осью OY.

6. Найдем точки максимума и минимума

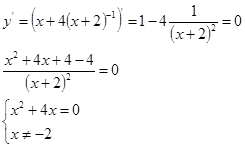
в точке производная меняет знак с <-> на <+>, следовательно имеем минимум, в точке производная меняет знак с <+> на <->, имеем максимум.

При первая производная отрицательна, следовательно, функция убывает, при производная положительна, функция в этих промежутках возрастает.

7. Найдем точки перегиба

, точек перегиба нет. При вогнутость вверх, при , вогнутость вниз.

8. Найдем горизонтальные и наклонные асимптоты в виде , где

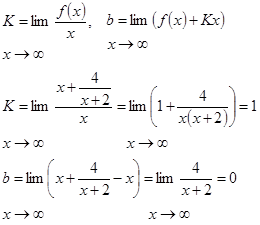
Получили асимптоту у=х.

Найдем пересечение кривой с асимптотой

Точек пересечения нет.

Строим график