Название: Графическое представление графа

Вид работы: лабораторная работа

Рубрика: Математика

Размер файла: 29.23 Kb

Скачать файл: referat.me-215975.docx

Краткое описание работы: Алгоритм перехода к графическому представлению для неориентированного графа. Количество вершин неориентированного графа. Чтение из матрицы смежностей. Связи между вершинами в матрице. Задание координат вершин в зависимости от количества секторов.

Графическое представление графа

Московский Авиационный Институт

(Государственный Технический Университет)

филиал «Восход»

Кафедра МиПОИС

Лабораторная работа

по дискретной математике

«Графическое представление графа»

(отчет)

Преподаватель ____________ /Крохина Н.В./

Студент группы ДМ 2-26 ___________ /Толоконников А.В./

г. Байконур

2002 г.

1. Задача

Составить алгоритм перехода к графическому представлению для неориентированного графа и реализовать его программным путем, если граф задан матрицей смежностей.

2. Алгоритм решения, поставленной задачи

1) Вводится количество вершин неориентированного графа.

2) Если количество вершин больше 7, то переходим к пункту 3; иначе переходим к пункту 4.

3) Генератором случайных чисел произвольно задаются связи между вершинами в матрице смежностей, переходим к пункту 5.

4) Вводятся связи между вершинами, исходя из следующего условия: не существует пути длиной в одно ребро из одной вершины в другую – ставим «0», существует путь между двумя вершинами длиной в одно ребро – ставим «1», существует путь из вершины в саму себя – ставим «2». Все введенные данные заносятся в матрице смежностей.

5) В зависимости от количества введенных вершин производится разбиение экрана на N секторов относительно центра экрана.

6) На граничных линиях секторов на одинаковом удалении от центра экрана выводим вершины.

7) Производим чтение из матрицы смежностей. Если связь между вершинами есть, то выводим на экран отрезок, соединяющий одну вершину с другой, если связи нет - рассматриваем следующую связь. Если связь циклическая изменяем цвет вершины с зеленого на коричневый.

3. Распечатка программы решения задачи

ProgramGraphs;

UsesCrt, Graph;

Const

M=25; {Предельное число вершин графа}

R=200; {Радиус окружности, на которой лежат вершины (центры окружностей)}

Type

Koor = Record

X,Y: Integer

End;

MasKoor = Array[1..M] Of Koor;

Smezno = Array[1..M,1..M] of Integer;

Var

Driver, Mode,

N,I,J: Integer; {Количество вершин графа}

A: MasKoor;

B: Smezno;

Procedure Koordinata; {Процедура задания координат вершин в зависимости от количества секторов}

Var

Q,W: Real;

Begin

Writeln('Введите количество вершин графа: ');

Readln(N);

If N>M Then Halt;

Q:=6.28/N;

{Задание координат вершин графа}

For I:=1 To N Do

Begin

W:=I*Q;

A[I].X:=300+Trunc(R*cos(W));

A[I].Y:=235+Trunc(R*sin(W));

End

End;

Procedure Vivod; {Выводвершинграфанаэкранмонитора}

Begin

For I:=1 To N Do

Begin

SetBkColor(0);

SetColor(2);

For J:=1 To 10 Do

Circle(A[I].X,A[I].Y,J)

End

End;

Procedure Smegnost; {Процедуразаданияматрицысмежностей}

Begin

For I:=1 To N Do

For J:=1 To N Do

B[I,J]:=9;

If N>7 Then

For I:=1 To N Do

For J:=1 To N Do

B[I,J]:=Random(3)

else

Begin

For I:=1 To N Do

For J:=1 To N Do

If B[I,J]=9 Then

Begin

Write('Введитесвязь [',I,',',J,']:= ');

Readln(B[I,J]);

B[J,I]:=B[I,J]

End

Else Writeln('Cвязь [',I,',',J,']:= ',B[I,J]);

End

End;

Procedure Linia;

Var K: Integer;

Begin

For I:=1 To N Do

For J:=1 To N Do

If (I=J) And (B[I,J]=2) Then {Циклическаясвязь}

Begin

SetColor(Brown);

For K:=1 To 10 Do

Circle(A[I].X,A[I].Y,K)

End else

If B[I,J]=1 Then {Обычнаясвязь}

Begin

SetColor(Red);

Line(A[I].X,A[I].Y,A[J].X,A[J].Y)

End

End;

{------------------------------------------------------------------}

Begin

ClrScr;

WriteLn('Вывод изображения графа на экран монитора');

Koordinata;

Smegnost;

Readln; {Задержкаэкрана}

Driver:=Detect;

InitGraph(Driver,Mode,'Egavga.bgi'); {Подключениеграфическогорежима}

Vivod;

Linia;

Readln;

Closegraph; {Отключение графического режима}

End.

неориентированный граф вершина матрица

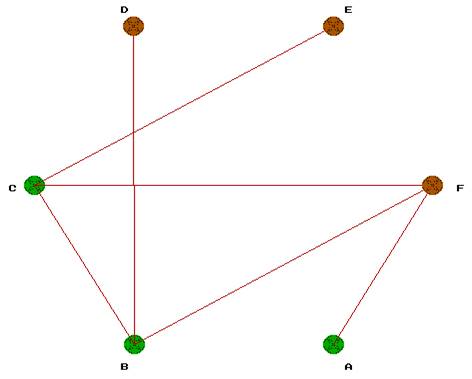
4. Результаты работы программы для числа вершин равного 6

Матрица смежностей вершин
A	B	C	D	E	F
A	0	0	1	0	0	1
B	0	0	1	1	0	1
C	0	1	0	0	1	1
D	1	0	1	2	1	0
E	0	0	1	0	2	0
F	1	0	1	0	1	2