Название: Графы Основные понятия
Вид работы: лабораторная работа
Рубрика: Математика
Размер файла: 83.01 Kb
Скачать файл: referat.me-214742.docx
Краткое описание работы: Министерство образования и науки Российской Федерации Курский государственный технический университет Кафедра ПО ВТ и АС Лабораторная работа № 1 Графы. Основные понятия
Графы Основные понятия
Министерство образования и науки Российской Федерации
Курский государственный технический университет
Кафедра ПО ВТ и АС
Лабораторная работа № 1
Графы. Основные понятия
Выполнил: студент гр. ПО 62 Шиляков И.А.
Проверил: доцентТомакова Р.А.
Курск 2007
Задание:
1. По заданным матрицам смежности вершин восстановить графы.
2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
4. Найти композицию графов 
.
5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
7. Определить хроматические и цикломатические числа данных графов.
8. Найти все базы графа.
9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Выполнение:
1. По заданным матрицам смежности вершин восстановить графы.
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
| x1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| x2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
| x3 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
| x4 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
| x5 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
| x6 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
| x7 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
A1
|
G1 (X1 ,A1 )
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
| x1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
| x2 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
| x3 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| x4 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
| x5 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| x6 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
| x7 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
A2
|
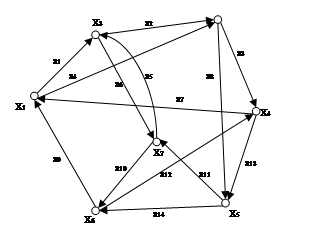
G2 (X2 ,A2 )
2. Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
| а1 |
а2 |
а3 |
а4 |
а5 |
а6 |
а7 |
а8 |
а9 |
а10 |
а11 |
а12 |
а13 |
а14 |
|
| а1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| а2 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
| а3 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| а4 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
| а5 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| а6 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
| а7 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
| а8 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
| а9 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
| а10 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
| а11 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
| а12 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
| а13 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
| а14 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
B1
| а1 |
а2 |
а3 |
а4 |
а5 |
а6 |
а7 |
а8 |
а9 |
а10 |
а11 |
а12 |
а13 |
а14 |
|
| а1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| а2 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| а3 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
| а4 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
| а5 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
| а6 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
| а7 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
| а8 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
| а9 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
| а10 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
| а11 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
| а12 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
| а13 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
| а14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
B2
| а1 |
а2 |
а3 |
а4 |
а5 |
а6 |
а7 |
а8 |
а9 |
а10 |
а11 |
а12 |
а13 |
а14 |
|
| x1 |
1 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
| x2 |
-1 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| x3 |
0 |
0 |
-1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
| x4 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
| x5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
-1 |
0 |
| x6 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
-1 |
| x7 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
1 |
S1
| а1 |
а2 |
а3 |
а4 |
а5 |
а6 |
а7 |
а8 |
а9 |
а10 |
а11 |
а12 |
а13 |
а14 |
|
| x1 |
1 |
0 |
0 |
1 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
| x2 |
0 |
-1 |
1 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| x3 |
-1 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| x4 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
| x5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
-1 |
1 |
| x6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
0 |
-1 |
| x7 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
S2
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
| x1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
| x1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
R1 R2
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
| x1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
| x1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| x7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Q1 Q2
3. Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
Объединение графов
G3 (X3 ,A3 )=G1 (X1 ,A1 ) YG2 (X2 ,A2 ); X3 = X1 YX2, A3 = A1 YA2
Пересечение графов
G3 (X3 ,A3 )=G1 (X1 ,A1 ) ∩G2 (X2 ,A2 ); X3 = X1 ∩X2, A3 = A1 ∩A2
Кольцевая сумма графов
G3
(X3
,A3
)=G1
(X1
,A1
)
G2
(X2
,A2
)
4. Найти и построить композицию графов 
.
| G1 (Х) |
G2 (Х) |
G1 (G2 (Х)) |
G2 (G1 (Х)) |
|
| x1 |
(x1 ,x2 ), (x1 ,x7 ) |
(x1 ,x2 ), (x1 ,x3 ) |
(x1 ,x3 ), (x1 ,x6 ), (x1 ,x2 ), (x1 ,x4 ), |
(x1 ,x4 ), (x1 ,x5 ), (x1 ,x3 ), (x1 ,x6 ), |
| x2 |
(x2 ,x3 ), (x2 ,x6 ) |
(x2 ,x4 ), (x2 ,x5 ) |
(x2 ,x1 ), (x2 ,x5 ), (x2 ,x7 ), |
(x2 ,x2 ), (x2 ,x7 ), (x2 ,x1 ), (x2 ,x4 ), |
| x3 |
(x3 ,x2 ), (x3 ,x4 ) |
(x3 ,x2 ), (x3 ,x7 ) |
(x3 ,x3 ), (x3 ,x6 ), (x3 ,x5 ), |
(x3 ,x4 ), (x3 ,x5 ), (x3 ,x1 ), |
| x4 |
(x4 ,x1 ), (x4 ,x5 ) |
(x4 ,x1 ), (x4 ,x5 ) |
(x4 ,x2 ), (x4 ,x7 ), (x4 ,x1 ), |
(x4 ,x2 ), (x4 ,x3 ), (x4 ,x6 ), (x4 ,x7 ), |
| x5 |
(x5 ,x1 ), (x5 ,x7 ) |
(x5 ,x6 ), (x5 ,x7 ) |
(x5 ,x3 ), (x5 ,x4 ), (x5 ,x5 ), (x5 ,x6 ), |
(x5 ,x2 ), (x5 ,x3 ), (x5 ,x6 ), |
| x6 |
(x6 ,x3 ), (x6 ,x4 ) |
(x6 ,x1 ), (x6 ,x4 ) |
(x6 ,x2 ), (x6 ,x7 ), (x6 ,x1 ), (x6 ,x5 ), |
(x6 ,x2 ), (x6 ,x7 ), (x6 ,x1 ), (x6 ,x5 ), |
| x7 |
(x7 ,x5 ), (x7 ,x6 ) |
(x7 ,x3 ), (x7 ,x6 ) |
(x7 ,x2 ), (x7 ,x4 ), (x7 ,x3 ), |
(x7 ,x6 ), (x7 ,x7 ), (x7 ,x1 ), (x7 ,x4 ), |
G1
(G2
(Х))
G2 (G1 (Х))
5. Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
Остовные подграфы
G’1 (X1 ,A1 )
G’2 (X2 ,A2 )
Произвольные подграфы
G1 ’’ (X1 ’’,A1 ’’)
|
G2
’’ (X2
’’,A2
’’) Порожденные подграфы
|
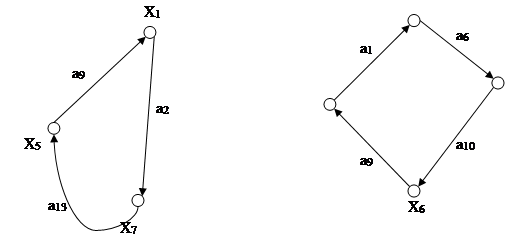
G1P (X1P ,A1P ) G2P (X2P ,A2P )
6. Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
Локальные степени графа G1
1
(х1
)=2 ; 2
(х1
)=2 ; (х1
)=4 ;
1
(х2
)=2 ; 2
(х2
)=2 ; (х2
)=4 ;
1
(х3
)=2 ; 2
(х3
)=2 ; (х3
)=4 ;
1
(х4
)=2 ; 2
(х4
)=2 ; (х4
)=4 ;
1
(х5
)=2 ; 2
(х5
)=2 ; (х5
)=4 ;
1
(х6
)=2 ; 2
(х6
)=2 ; (х6
)=4 ;
1
(х7
)=2 ; 2
(х7
)=2 ; (х7
)=4 ;
Локальные степени графа G2
1
(х1
)=2 ; 2
(х1
)=2 ; (х1
)=4 ;
1
(х2
)=2 ; 2
(х2
)=2 ; (х2
)=4 ;
1
(х3
)=3 ; 2
(х3
)=2 ; (х3
)=4 ;
1
(х4
)=2 ; 2
(х4
)=2 ; (х4
)=4 ;
1
(х5
)=2 ; 2
(х5
)=2 ; (х5
)=4 ;
1
(х6
)=2 ; 2
(х6
)=2 ; (х6
)=4 ;
1
(х7
)=2 ; 2
(х7
)=2 ; (х7
)=4 ;
Эйлерова цепь существует в двух графах, т.к. все локальные степени графов четны.
Эйлеров цикл существует в двух графах, т.к. все локальные степени графов четны.
7. Определить хроматические и цикломатические числа данных графов.
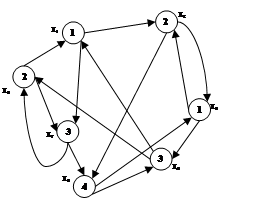
Хроматическое число γ для графа G1 = 4
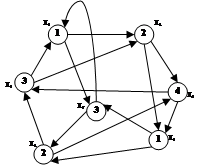
Хроматическое число γ для графа G2 = 4
Цикломатические числа графов
V(G1 )=m-n+r, где m - число рёбер (дуг);
n – число вершин;
r – число компонент связности.
V(G1 )=14-7+1=8;
V(G2 )=14-7+1=8;
8. Найти все базы графа.
Базы графа G1
B1 ={x1 }
B2 ={x2 }
B3 ={x3 }
B4 ={x4 }
B5 ={x5 }
B6 ={x6 }
B7 ={x7 }
Базы графа G2
B1 ={x1 }
B2 ={x2 }
B3 ={x3 }
B4 ={x4 }
B5 ={x5 }
B6 ={x6 }
B7 ={x7 }
9. Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Сильные компоненты связности G1
СК={x1 , x2 , x3 , x4 , x5 , x6 , x7 }
Сильные компоненты связности G2
СК={x1 , x2 , x3 , x4 , x5 , x6 , x7 }
Конденсация графа G1 Конденсация графа G2
Похожие работы
-
Колебательно движение материальной точки
Министерство образования и науки Российской Федерации Санкт-Петербургский государственный горный институт имени В.Г. Плеханова (технический университет)
-
Проверка больших чисел на простоту
Министерство образования Республики Беларусь Учреждение образования «Брестский государственный технический университет» Кафедра ИИТ Лабораторная работа №4
-
Математическая логика и теория алгоритмов 3
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
-
Математика
Министерство науки, высшей школы и технической политики Российской Федерации. Новосибирский Государственный Технический Университет. Контрольная работа по специальным главам математики.
-
Вычисление корней нелинейного уравнения
Министерство образования Российской федерации Южно-Уральский Государственный Университет Аэрокосмический факультет Кафедра летательных аппаратов
-
Вычисление координат центра тяжести плоской фигуры
Министерство общего и профессионального образования Российской федерации. Уральский Государственный Технический Университет - УПИ. Реферат ВЫЧИСЛЕНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ.
-
Дифференциальные уравнения для электрической цепи
Министерство Образования Российской Федерации ИрГТУ Кафедра АПП Курсовая работа по математике Выполнил: студент группы АТП-05-1 Поверил: профессор
-
Преимущества и недостатки систем с отрицательной обратной связью
Федеральное агентство по образованию Российской Федерации Министерство образования и науки Российской Федерации Кафедра "Экономика и управление проектами"
-
Интерполяция функций 2
Министерство образования Российской Федерации. Хабаровский государственный Технический Университет. Кафедра «Прикладная математика и информатика»
-
Однополостный гиперболоид
Министерство высшего образования Российской Федерации Московский государственный строительный университет РЕФЕРАТ На тему: “Однополостный гиперболоид”