Название: Площадь треугольника
Вид работы: реферат
Рубрика: Математика
Размер файла: 56.24 Kb
Скачать файл: referat.me-216155.docx
Краткое описание работы: Задача Дано: треугольник с вершинами в точках А [4; 0] B [3; 20] [5; 0]. Найти: a) Уравнение прямой b) Уравнение высоты , проведенной к стороне c) Уравнение прямой
Площадь треугольника
Задача
Дано: треугольник с вершинами в точках А [4; 0] B [3; 20] и C [5; 0].
Найти:
a) Уравнение прямой АВ ;
b) Уравнение высоты С D , проведенной к стороне АВ ;
c) Уравнение прямой СЕ , параллельной стороне АВ;
d) Площадь треугольника АВС
Решение:
А) Уравнение прямой АВ найдем по формуле:
![]() , где
, где
X 1 , Y 1 – координаты первой точки,
X 2 , Y 2 – координаты второй точки.
![]()
![]()
![]()
В) Уравнение высоты С D найдем, используя следующий алгоритм:
1. Найдем угловой коэффициент[1] , используя условие перпендикулярности прямых[2] :
![]() , где
, где
K 1 – угловой коэффициент прямой АВ
K2 – угловой коэффициент прямой С D
![]()
2. Найдем уравнение прямой с угловым коэффициентом k 2 , проходящая через точку С [5; 0]:
![]() , где
, где
X 1 , Y 1 – координаты точки,
![]()
![]()
C) Уравнение прямой СЕ найдем, используя следующий алгоритм:
1. Найдем угловой коэффициент, используя условие параллельности прямых:
![]() , где
, где
K 1 – угловой коэффициент прямой АВ
K 2 – угловой коэффициент прямой СЕ
![]()
2. Найдем уравнение прямой с угловым коэффициентом k2 , проходящая через точку С [5; 0]:
![]() , где
, где
X 1 , Y 1 – координаты точки,
![]()
![]()
D) Найдем площадь треугольника по формуле:
![]()
1. Найдем длину стороны АВ по формуле:
![]() , где
, где
X 1 , Y 1 – координаты точки А ,
X 2 , Y 2 – координаты точки В ,
![]()
2. Найдем длину стороны СD по формуле:
![]() , где
, где
X 0 , Y 0 – координаты точки С ,
А, B , C – коэффициенты прямой АВ (Ах+Ву+С – уравнение прямой).
Уравнение прямой АВ ![]() или
или ![]()
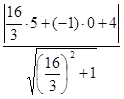
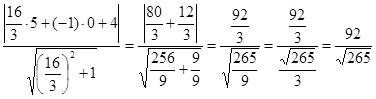
3. Найдем площадь S:
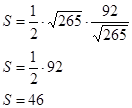
[1] Угловой коэффициент прямой — коэффициент k в уравнении y = kx + b прямой на координатной плоскости
[2] Высота треугольника (С D )— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону (AB )
Похожие работы
-
Вписанные и описанные окружности в треугольниках и четырехугольниках
Реферат по геометрии на тему «Вписанные и описанные окружности в треугольниках и четырехугольниках 2009 год Цели: Углубить знания по теме «Вписанная и описанная окружности в треугольниках и четырехугольниках»
-
Некоторые вопросы геометрии вырожденных треугольников
Применение методов векторной алгебры позволяет выявлять те особые свойства фигур, которые могут ускользнуть от нас при их наглядно-геометрическом рассмотрении, и при этом не потерять геометрическую наглядность изучаемого факта.
-
Элементы планиметрии
Цель предлагаемого задания – повторить материал по планиметрии для дальнейшего его использования при решении задач по стереометрии, а также применения при решении олимпиадных задач.
-
Математические уравнения и функции
Варивант №2 адание 1 Дан треугольник ABC, где А(-3,2), В(3,-1), С(0,3). Найти: 1. Длину стороны АВ; 2. Внутренний угол А с точностью до градуса; 3. Уравнение и длину высоты, опущенной из вершины С;
-
Решение задач по высшей математике
Задача 10 Даны матрицы Найти матрицу С = 5В – АE + BA -2Е Решение: 2 -1 1 1 1 2 BA= 3 4 -2 · -2 0 2 1 0 -1 0 -1 0 2•1+(-1)•(-2)+1•0 2•1+(-1)•0+1•(-1) 2•2+(-1)•2+1•0 3•1+4•(-2)+(-2)•0 3•1+4•0+(-2)•(-1) 3•2+4•2+(-2)•0
-
Решение линейной системы уравнений с тремя неизвестными
Решение системы линейных уравнений двумя способами: по формулам Крамера и методом Гаусса. Решение задачи на нахождение производных, пользуясь правилами и формулами дифференцирования. Исследование заданных функций методами дифференциального исчисления.
-
Прямая Эйлера
Теорема о пересечении медиан треугольника в одной точке. Теорема о высотах произвольного треугольника. Медианы и высоты тетраэдра, прямая Эйлера тетраэдра.
-
Окружности в треугольниках и четырехугольниках
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 8 Реферат по геометрии на тему: Окружности в треугольниках и четырехугольниках
-
Линейные функции
Общее уравнение прямой, переходящей через определенную точку. Условия перпендикулярности прямых. Условие перпендикулярности плоскостей. Свойства медианы треугольника. Нахождение направляющих векторов прямых. Условие параллельности прямой и плоскости.
-
Решение математических уравнений и функций
Вариант 1 Задание 1 Дан треугольник АВС: А(5;4), В(2;0), С(8;3). Найти: длину стороны АВ; внутренний угол А с точностью до градуса; уравнение и длину высоты, опущенной из вершины С;