Название: Закон Грэма

Вид работы: доклад

Рубрика: Математика

Размер файла: 16.16 Kb

Скачать файл: referat.me-216471.docx

Краткое описание работы: Чем меньше плотность идеального газа, тем больше скорость его истечения через микроскопические отверстия в стенках сосуда.

Закон Грэма

Томас ГРЭМ (Thomas Graham, 1805–69)

Шотландский химик. Родился в Глазго в семье преуспевающего фабриканта. Вопреки воле отца, желавшего видеть сына священником, он решил изучать химию. По окончании учебы в университете Глазго работал в разных научных учреждениях (даже был, как и когда-то Исаак Ньютон, директором Монетного двора). Томас Грэм известен в научном мире как основатель коллоидной химии (коллоиды — что-то вроде растворов, в которых частицы намного больше молекул).

Чем меньше плотность идеального газа, тем больше скорость его истечения через микроскопические отверстия в стенках сосуда

Эффузия — это процесс медленного истечения газов через маленькие (часто микроскопические) отверстия. Вы встречались с явлением эффузии, когда наутро после празднования дня рождения обнаруживали вдруг, что наполненные накануне гелием воздушные шарики сдулись. Пока вы спали, через микроскопические поры гелий вытек из шариков.

1829 году Томас Грэм провел серию экспериментов по эффузии и обнаружил, что при постоянных температуре и давлении скорость истечения газа r обратно пропорциональна квадратному корню из плотности газа d. На языке уравнений это выглядит следующим образом:

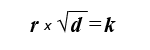
где k — константа. Другими словами, чем выше плотность газа при постоянных температуре и давлении, тем ниже скорость эффузии. Пожалуй, самое удивительное в законе Грэма — это то, что постоянная k (в правой части приведенного выше уравнения) при равных условиях примерно одинакова для всех газов.

Как мы знаем из законов идеального газа, при постоянных температуре и давлении плотность газа пропорциональна его относительной молекулярной массе M. Исходя из этого, можно переписать уравнение закона Грэма следующим образом:

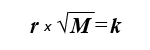
Теперь закон об относительной скорости истечения разных газов из одинаковых сосудов мы можем сформулировать так: чем меньше относительная молекулярная масса газа, тем выше скорость эффузии. Вот почему резиновый воздушный шарик, наполненный гелием (с относительной молекулярной массой 4), сдуется за одну ночь, но если тот же шарик наполнить воздухом, то есть смесью главным образом азота (относительная молекулярная масса 28) и кислорода (относительная молекулярная масса 32), он останется надутым в течение нескольких дней. (Воздушные шарики из металлизированной пленки, у которой поры значительно меньше, чем у резины, могут удерживать гелий в течение нескольких недель.)

Это может показаться неожиданным, но закон Грэма нашел применение и при конструировании космических кораблей, предназначенных для длительного нахождения человека в космосе. Корабль, конечно, отличается от воздушного шарика, но с течением времени воздух будет просачиваться через материал, из которого сделан корпус, так же, как он просачивается через оболочку шарика. Может быть, это и не главная забота тех, кто думает о будущем человечества в космосе, но в конце концов с этим придется считаться, например придумав способ получения газов прямо на борту корабля, чтобы компенсировать потери в безвоздушное пространство.