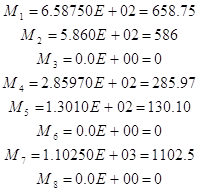Referat.me
/ / Системы уравнений межотраслевого баланса

Название: Системы уравнений межотраслевого баланса

Вид работы: реферат

Рубрика: Математика

Размер файла: 230.25 Kb

Скачать файл: referat.me-216487.docx

Краткое описание работы: Выработать у студентов навыки построения математических моделей межотраслевого баланса в статистических случаях и оптимизации моделей в рамках межотраслевого баланса. Научиться делать выводы в рамках построения моделей.

Системы уравнений межотраслевого баланса

Лабораторную работу выполнил Сиропов Вадим Александрович

Южно-Российский государственный университет экономики и сервиса

Цели:

Выработать у студентов навыки построения математических моделей межотраслевого баланса в статистических случаях и оптимизации моделей в рамках межотраслевого баланса. Научиться делать выводы в рамках построения моделей.

Задание:

Найти объемы выпуска продукции по каждой из отраслей, предварительно обосновав сущность нестандартного решения.

Рассчитать новый план выпуска продукции, при условии, что конечный спрос на продукцию U-ой и -ой отраслей возрос соответственно на 85 и 97 единиц. Вычислить абсолютные и относительные приросты объема, выполненные по каждой из отраслей.

Скорректировать новый план, с учетом того, что отрасль не может увеличить объемы выпуска своей продукции более чем на 2 единицы.

Рассчитать матрицу полных затрат.

Исходные данные:

A =

0.02

0.01

0.01

0.05

0.06

0.03

0.05

0.02

0.01

0.01

0.09

0.06

0.04

0.08

0.05

0.06

0.06

0.05

0.04

0.05

0.06

0.04

0.08

0.03

0.05

 C =

235

194

167

209

208

, , .

0) Проверим матрицу А на продуктивность:

Матрица А является продуктивной матрицей.

(J-A) =

J – единичная матрица;

A – заданная матрица прямых затрат;

- вектор (план) выпуска продукции, подлежащей определению;

- вектор конечного спроса.

Произведем расчеты на PС, используя метод Гаусса.

; ;

;

;

;

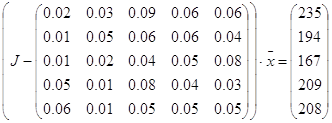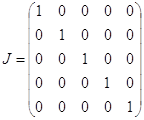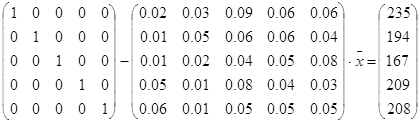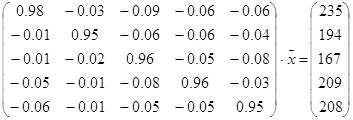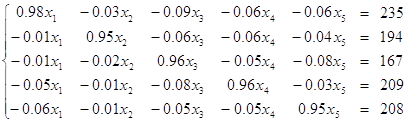Используя Симплекс-метод, получим:

2)

;

;

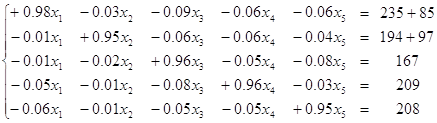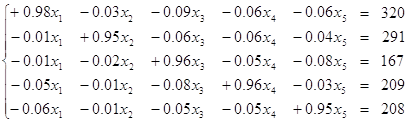Решение:

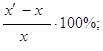
3) Скорректировать новый план, с учетом того, что отрасль не может увеличить объем выпуска своей продукции, более чем на 2 единицы.

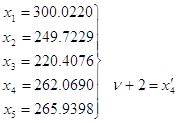
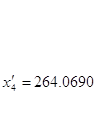
Подставляя значение в исходную систему уравнений, получим:

;

;

;

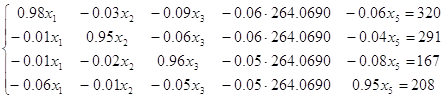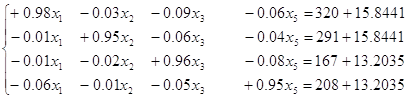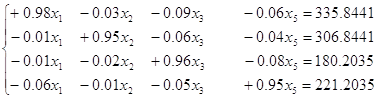Решаем систему уравнений методом Гаусса:

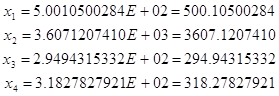
4) Рассчитаем матрицу полных затрат.

Произведем обращение матрицы:

.

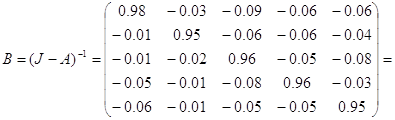
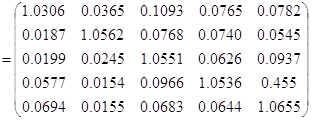Матрица, вычисленная вручную:

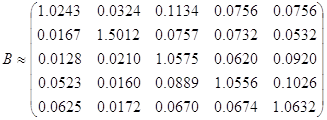
Вывод: Видно, что несмотря на сходство этих матриц, полученные приближенные значения довольно грубы.

Рассчитаем деревья матрицы:




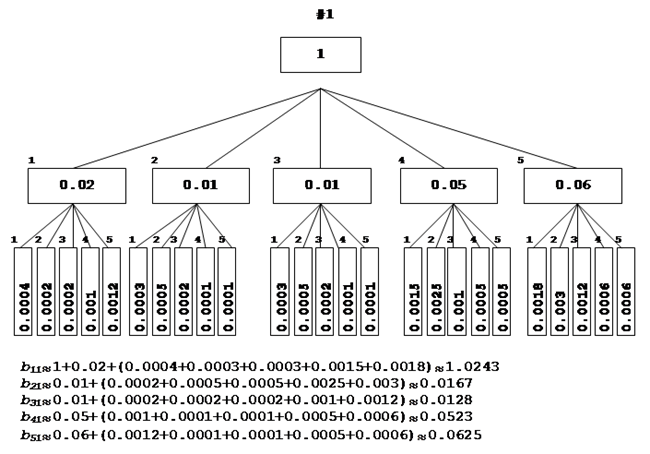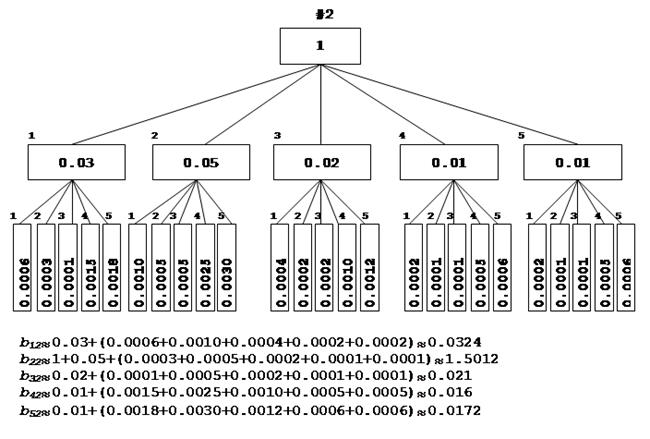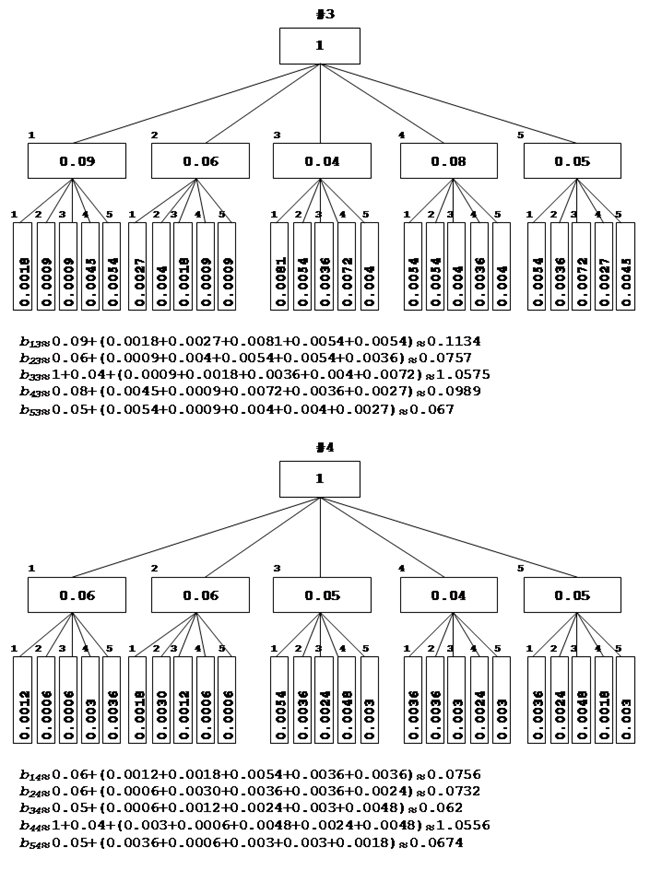
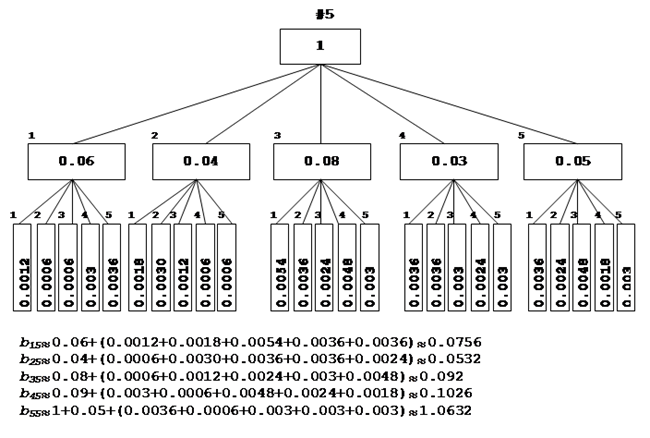
Оптимизационная модель межотраслевого баланса.

Зная запасы дополнительных ресурсов (r), нормы их затрат (D) на производство продукции каждой отрасли и цены реализации конечной продукции (p), рассчитать объемы производства продукции, обеспечивающие максимальный фонд конечного спроса. Вычислить конечный спрос и провести анализ полученного решения:

относительно оптимальности;

статуса и ценности ресурсов;

чувствительности.

Рассчитать объем производства.

Исходные данные:

D =

0.3

0.6

0.5

0.6

0.6

0.9

0.5

0.8

0.1

0.9

0.4

0.8

1.1

0.2

0.7

= 564

298

467

= (121 164 951 254 168)

Требуется максимизировать цену конечного спроса;

=

:

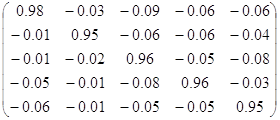, при ограничениях:

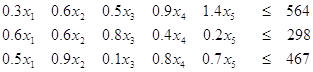
Решая задачу на ЭВМ, симплекс-методом, получим:

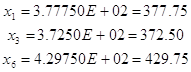
Решим соответствующую двойственную задачу:

;

;

;

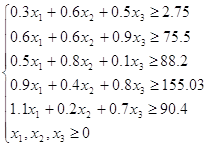
Решая задачу на ЭВМ, симплекс-методом, получим:

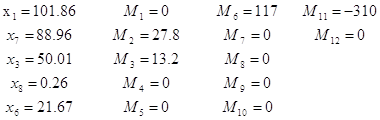
Проведем анализ результатов:

1) Оптимальность:

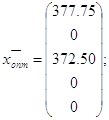
т.е., следует выпускать лишь продукцию 1-ой и 3-ей отрасли, объем которой соответственно составит – 377,75 и 372,50 ед. Не следует выпускать продукцию 2-ой, 4-ой и 5-ой отрасли.

Оптовая цена конечного спроса:

=

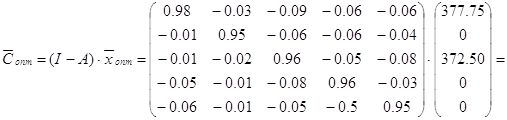
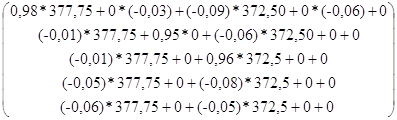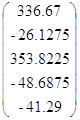
т.е. С1=336.67, С2=-26.1275, С3=353.8225, С4=-48.6875, С5=-41.29,

отрицательные значения говорят о том, что продукция отраслей необходимая для функционирования.

2) Статус и ценность ресурсов:

Ресурс Остаточная переменная Статус ресурса Теневая цена
1 x6 = 21,67 недефицитный 0
2 X7 = 88,96 недефицитный 0
3 X8 = 0,26 недефицитный 0

Похожие работы

  • Динамические линейные модели экономики модель динамического межотраслевого баланса и модель Ней

    Содержание Введение Динамические модели экономики — модели, описывающие экономику в развитии (в отличие от статических, характеризующих ее состояние в определенный момент). Модель является динамической, если, как минимум, одна ее переменная относится к периоду времени, отличному от времени, к которому отнесены другие переменные.

  • Балансовые модели

    СОДЕРЖАНИЕ Балансовые модели. 2 1. Балансовый метод. Принципиальная схема межпродуктового баланса. 2 2. Экономико-математическая модель межотраслевого баланса. 8

  • Моделирование макроэкономических процессов и систем

    Оглавление Введение Задание 1 Задание 2 Задание 3 Задание 4 Задание 5. Динамическая экономико-математическая модель Кейнса Экономика в форме динамической модели Кейнса как инерционное звено

  • Модель межотраслевого баланса продукции

    Федеральное агентство по образованию Пермский государственный технический университет КУРСОВАЯ РАБОТА по дисциплине «Экономико-математические методы и модели»

  • Применение балансового метода для решения экономических задач

    ВВЕДЕНИЕ Балансовый метод позволяет выбрать оптимальное соотношение между различными отраслями социально-экономического комплекса региона. Балансы используются для разработки рациональных внутрирегиональных и межрегиональных связей. Составление балансов (отраслевых, региональных, межрегиональных) способствует установлению уровня комплексного развития региона, определению диспропорций в его развитии.

  • по Экономико-математическим моделям

    ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ КАФЕДРА ЭММ Контрольная работа по дисциплине «Экономико-математическим моделям» Вариант № 1

  • по линейной алгебре

    Министерство образования РФ Московский государственный университет сервиса Региональный институт сервиса Контрольная работа по математике Выполнил студент 1 курса

  • Общее представление о математическом моделировании экономических задач

    1. Общее представление о математическом моделировании экономических задач 1.1. Определение экономико-математической модели Математические модели экономических задач – это совокупность средств: уравнений, комплексов математических зависимостей, знаковые логические выражения, отображающие выделенные для изучения характеристики объекта, реальные взаимосвязи и зависимости экономических показателей.

  • Математические модели в экономике

    Факультет дистанционного обучения Томский государственный университет систем управления и радиоэлектроники (ТУСУР) Кафедра экономики Контрольная работа № 1

  • Аналитическая геометрия в решении экономических задач

    Расчет эффективности ведения многоотраслевого хозяйства, отображение связей между отраслями в таблицах балансового анализа. Построение линейной математической модели экономического процесса, приводящей к понятию собственного вектора и значения матрицы.