Referat.me
/ / Эконометрика

Название: Эконометрика

Вид работы: реферат

Рубрика: Математика

Размер файла: 181.01 Kb

Скачать файл: referat.me-216497.docx

Краткое описание работы: Обработка результатов наблюдений за дневной выручкой восьми продавцов на рынке.

Эконометрика

Контрольная работа

Выполнила студентка Бродниковская Надежда Григорьевна

Московский институт международных экономических отношений (факультет заочного обучения)

2001г.

1. Наблюдения за дневной выручкой восьми продавцов на рынке дали следующие результаты:

Выручка,

Тыс.у.е.

 12 13 15 16 18
Число продавцов 1 1 3 2 1

а) Определить вероятность того, что средняя выручка по всему рынку будет отличаться от среднего восьми продавцов не более чем на 2,5 тыс.у.е.

Найти среднюю выручку

средняя выручка

среднее отклонение

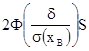
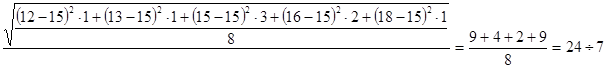
d=2,5 U=2,89= 0,993 0,998

б) С вероятностью найти доверительный интервал для генерального среднего выручки M(X).

значение t=0,95t=1,65

d=2,31 доверительный интервал.

2. Используя метод средней, построить зависимость типа y=ax+b, если результаты наблюдений представлены таблицами:

а)

1 2 3 4 5
3,2 4,2 2,7 0,7 1,5

у=ax+b a

m=2 n=5

3a+2b=7,4

12a+3b=4,9


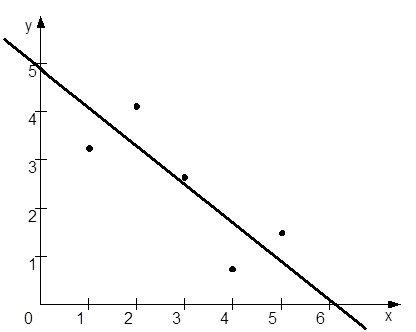
б)

xi 1 2 3 4 5 6
yi 1,3 2,5 0,8 3,8 1,8 3,6

m=3 n=6 6a+3b=4,6

m=3 n=15 15a+3b=9,2

6=


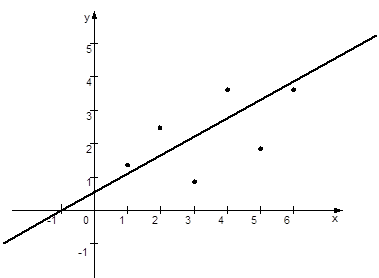3. Путем расчета коэффициента корреляции доказать, что между X и Y существует линейная корреляция. Методом наименьших квадратов найти уравнение прямой линии регрессии, построить графики корреляционных зависимостей и оценить адекватность регрессионных моделей.

а)

xi 1,0 4,1 3,8 3,9 1,2 3,9 4,1 0,8 0,7 1,3
yi 23,6 31,9 35,2 36,4 23,6 34,0 38,2 17,3 28,8 19,7

a= 11,64-0,4b 3,38(11,64-0,4b)+b=32,55 39,34-1,35b+b=32,55

-0,35b=-6,79 b=19,4 a=3,88

y=3,88x+19,4

XB =

N. XI YI XI -XB YI -YB
1 23,6 1 23,6 -1,48 -5,27 7,7996 2,1904 27,7729
4,1 31,9 16,81 130,79 1,62 3,03 4,9086 2,6244 9,1809
3,8 35,2 14,44 133,76 1,32 6,33 8,3656 1,7424 40,0689
3,9 36,4 15,21 141,96 1,42 7,53 10,6926 2,0164 56,7009
1,2 23,6 1,44 28,32 -1,28 -5,27 6,7456 1,6384 27,7729
3,9 34 15,21 132,6 1,42 5,13 7,2846 2,0164 26,3169
4,1 38,2 16,81 156,62 1,62 9,33 15,1146 2,6244 87,0489
0,8 17,3 0,64 13,84 -1,68 -11,57 19,4376 2,8224 133,8649
0,7 28,8 0,49 20,16 -1,78 -0,07 0,1246 3,1684 0,0049
1,3 19,7 1,69 25,61 -1,18 -9,17 10,8206 1,3924 84,0889
24,8 288,7 83,74 807,26 91,284 22,236 492,821

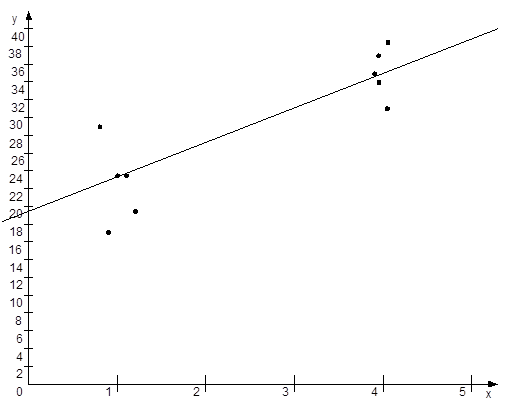Значение коэффициента детерминации равное 0,75 свидетельствует о средней связи между Х и У, и о среднем общем качестве построенного уравнения регрессии

б)

XI 3,0 1,1 2,9 3,0 0,8 1,5 2,1 3,2 1,2 3,0
YI 37,6 18,5 29,1 38,5 18,8 20,6 29,6 36,8 15,8 33,4

y=8,69x+8,9

N XI YI XI YI XI -XB YI -YB
1 3 37,6 9 112,8 0,82 9,73 7,9786 0,6724 94,6729
2 1,1 18,5 1,21 20,35 -1,08 -9,37 10,1196 1,1664 87,7969
3 2,9 29,1 8,41 84,39 0,72 1,23 0,8856 0,5184 1,5129
4 3 38,5 9 115,5 0,82 10,63 8,7166 0,6724 112,9969
5 0,8 18,8 0,64 15,04 -1,38 -9,07 12,5166 1,9044 82,2649
6 1,5 20,6 2,25 30,9 -0,68 -7,27 4,9436 0,4624 52,8529
7 2,1 29,6 4,41 62,16 -0,08 1,73 -0,1384 0,0064 2,9929
8 3,2 36,8 10,24 117,76 1,02 8,93 9,1086 1,0404 79,7449
9 1,2 15,8 1,44 18,96 -0,98 -12,07 11,8286 0,9604 145,6849
10 3 33,4 9 100,2 0,82 5,53 4,5346 0,6724 30,5809
11
12 21,8 278,7 55,6 678,06 70,494 8,076 691,101


Значение коэффициента детерминации равное 0,88 свидетельствует о средней связи между Х и У, и о среднем общем качестве построенного уравнения регрессии

4. Используя аксиомы метода наименьших квадратов вывести систему нормальных уравнений для теоретической линии регрессии вида: yx =ax2 +bx+c

yx-ax3 -bx2 -cx=0

yx=ax3 +bx2 +cx

y-ax2 -bx-c=0

Похожие работы

  • Аккредитация органов по сертификации и испытательных лабораторий

    Аккредитация — официальное признание органом по аккредитации компетентности физического или юридического лица выполнять работы в определенной области оценки соответствия (Закон РФ № 184-ФЗ «О техническом регулировании»).

  • Модель парной регрессии

    Содержание ТЕМА 1. Выборка и генеральная совокупность Задача 1 ТЕМА 2. Модель парной регрессии Задача 12 ТЕМА 3. Модель множественной регрессии Задача 13

  • Статистическая обработка результатов прямых многоразовых измерений с независимыми равноточными

    Розрахунково-графічне завдання з теми: «Статистична обробка результатів прямих багаторазових вимірювань з незалежними рівноточними спостереженнями»

  • Обработка статистических данных и установление закона распределения случайных величин

    ГОУ ВПО ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ кафедра «Управление эксплуатационной работой» Расчетно-графическая работа

  • Стабилизация денежного потока, теории фирмы

    Лабораторная работа №1 Стабилизация денежного потока Исходные данные Имеется N предприятий. Известно для каждого предприятия на начальный этап времени финансовое состояние предприятий: m

  • Раздел по Метрологии . Обработка результатов косвенных измерений

    Содержание Введение………………………………………………………………………2 1. Раздел по «Метрологии». Обработка результатов косвенных измерений…………………………………………………..4

  • Средние величины 3

    Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ 5.1. Понятие о средней величине Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистике используются различного рода средние величины.

  • Общее представление о математическом моделировании экономических задач

    1. Общее представление о математическом моделировании экономических задач 1.1. Определение экономико-математической модели Математические модели экономических задач – это совокупность средств: уравнений, комплексов математических зависимостей, знаковые логические выражения, отображающие выделенные для изучения характеристики объекта, реальные взаимосвязи и зависимости экономических показателей.

  • Построение математических моделей

    Составление математической модели для предприятия, характеризующей выручку предприятия "АВС" в зависимости от капиталовложений (млн. руб.) за последние 10 лет. Расчет поля корреляции, параметров линейной регрессии. Сводная таблица расчетов и вычислений.

  • Асимметричная информация на рынке

    Введение При рассмотрении конкурентного рынка, мы создаем идеальную, абстрактную модель – модель совершенной конкуренции. В ней создаются лабораторные условия, которые обеспечивают «чистоту эксперимента». Модель совершенной конкуренции предполагает следующие условия: множество покупателей и продавцов на рынке, свободное перемещение ресурсов, отсутствие барьеров для вступления в отрасль, однородная и стандартная продукция и симметричность информации.