Название: Все формулы по математике в школе

Вид работы: шпаргалка

Рубрика: Математика

Размер файла: 27.03 Kb

Скачать файл: referat.me-216677.docx

Краткое описание работы: Шпаргалка по школьной математике.

Все формулы по математике в школе

Формулы сокр. умножения и разложения на множители :

(a±b)?=a?±2ab+b?

(a±b)?=a?±3a?b+3ab?±b?

a?-b?=(a+b)(a-b)

a?±b?=(a±b)(a?∓ab+b?),

(a+b)?=a?+b?+3ab(a+b)

(a-b)?=a?-b?-3ab(a-b)

xⁿ -aⁿ =(x-a)(x^n-1 +ax^n-2 +a?x^n-3 +...+a^n-1 )

ax?+bx+c=a(x-x₁ )(x-x₂ )

где x₁ и x₂ — корни уравнения

ax?+bx+c=0

Степени и корни :

a^p ·a^g = a^p+g

a^p :a^g =a ^p-g

(a^p )^g =a ^pg

a^p /b^p = (a/b)^p

a^p ×b^p = ab^p

a⁰ =1; a¹ =a

a^-p = 1/a

^p Öa =b => b^p =a

^p Öa^p Öb = ^p Öab

Öa ; a ? 0

____

/ __ _

^p Ö^g Öa = ^pg Öa

___ __

^pk Öa^gk = ^p Öa^g

_p ____

/ a ^p Öa

/ ¾¾ = ¾¾¾¾

Ö b ^p Öb

a ^1/p = ^p Öa

^p Öa^g = a^{g/ p}

Квадратное уравнение

ax?+bx+c=0; (a¹0)

x_1,2 = (-b±ÖD)/2a; D=b? -4ac

D>0® x₁ ¹x₂ ;D=0® x₁ =x₂

D<0, корней нет.

Теорема Виета:

x₁ +x₂ = -b/a

x₁ × x₂ = c/a

Приведенное кв. Уравнение:

x? + px+q =0

x₁ +x₂ = -p

x₁ ×x₂ = q

Если p=2k (p-четн.)

и x?+2kx+q=0, то x_1,2 = -k±Ö(k?-q)

Нахождение длинны отр-ка

по его координатам

Ö((x₂ -x₁ )?-(y₂ -y₁ )?)

Логарифмы:

log_a x = b => a^b = x; a>0,a¹0

a ^{loga x} = x, log_a a =1; log_a 1 = 0

log_a x = b; x = a^b

log_a b = 1/(log _b a)

log_a xy = log_a x + log_a y

log_a x/y = log_a x - log_a y

log_a x^k =k log_a x (x >0)

log_a ^k x =1/k log_a x

log_a x = (log_c x)/( log_c a); c>0,c¹1

log_b x = (log_a x)/(log_a b)

Прогрессии

Арифметическая

a_n = a₁ +d(n-1)

S_n = ((2a₁ +d(n-1))/2)n

Геометрическая

b_n = b_n-1 × q

b² _n = b_n-1 × b_n+1

b_n = b₁ ×q^n-1

S_n = b₁ (1- qⁿ )/(1-q)

S= b₁ /(1-q)

Тригонометрия .

sin x = a/c

cos x = b/c

tg x = a/b=sinx/cos x

ctg x = b/a = cos x/sin x

sin (p-a) = sin a

sin (p/2 -a) = cos a

cos (p/2 -a) = sin a

cos (a + 2pk) = cos a

sin (a + 2pk) = sin a

tg (a + pk) = tg a

ctg (a + pk) = ctg a

sin?a + cos?a =1

ctg a = cosa / sina , a¹pn, nÎZ

tga× ctga = 1, a¹ (pn)/2, nÎZ

1+tg?a = 1/cos?a , a¹p(2n+1)/2

1+ ctg?a =1/sin?a , a¹pn

Формулы сложения:

sin(x+y) = sin x cos y + cos x sin y

sin (x-y) = sin x cos y - cos x sin y

cos (x+y) = cos x cos y - sin x sin y

cos (x-y) = cos x cos y + sin x sin y

tg(x+y) = (tg x + tg y)/ (1-tg x tg y )

x, y, x + y ¹p/2 + pn

tg(x-y) = (tg x - tg y)/ (1+tg x tg y)

x, y, x - y ¹p/2 + pn

Формулы двойного аргумента.

sin 2a = 2sin a cos a

cos 2a = cos?a - sin?a = 2 cos?a - 1 =

= 1-2 sin?a

tg 2a = (2 tga)/ (1-tg?a)

1+ cos a = 2 cos?a/2

1-cosa = 2 sin?a/2

tga = (2 tg (a/2))/(1-tg?(a/2))

Ф-лы половинного аргумента.

sin?a/2 = (1 - cos a)/2

cos?a/2 = (1 + cosa)/2

tg a/2 = sina/(1 + cosa ) = (1-cos a)/sin a

a¹p + 2pn, n ÎZ

Ф-лы преобразования суммы в произв.

sin x + sin y = 2 sin ((x+y)/2) cos ((x-y)/2)

sin x - sin y = 2 cos ((x+y)/2) sin ((x-y)/2)

cos x + cos y = 2cos (x+y)/2 cos (x-y)/2

cos x - cos y = -2sin (x+y)/2 sin (x-y)/2

sin (x+y)

tg x + tg y = —————

cos x cos y

sin (x - y)

tg x - tgy = —————

cos x cos y

Формулы преобр. произв. в сумму

sin x sin y = ?(cos (x-y) - cos (x+y))

cos x cos y = ?(cos (x-y)+ cos (x+y))

sin x cos y = ?(sin (x-y)+ sin (x+y))

Соотнош. между ф-ями

sin x = (2 tg x/2)/(1+tg² x/2)

cos x = (1-tg² 2/x)/ (1+ tg? x/2)

sin2x = (2tgx)/(1+tg² x)

sin?a = 1/(1+ctg?a) = tg?a/(1+tg?a)

cos?a = 1/(1+tg?a) = ctg?a / (1+ctg?a)

ctg2a = (ctg?a-1)/ 2ctga

sin3a = 3sina -4sin?a = 3cos?asina-sin?a

cos3a = 4cos?a-3 cosa=

= cos?a-3cosasin?a

tg3a = (3tga-tg?a)/(1-3tg?a)

ctg3a = (ctg?a-3ctga)/(3ctg?a-1)

sin a/2 = ±Ö((1-cosa)/2)

cos a/2 = ±Ö((1+cosa)/2)

tga/2 = ±Ö((1-cosa)/(1+cosa))=

sina/(1+cosa)=(1-cosa)/sina

ctga/2 = ±Ö((1+cosa)/(1-cosa))=

sina/(1-cosa)= (1+cosa)/sina

sin(arcsin a) = a

cos( arccos a) = a

tg ( arctg a) = a

ctg ( arcctg a) = a

arcsin (sina) = a ; aÎ [-p/2 ; p/2]

arccos(cos a) = a ; aÎ [0 ; p]

arctg (tg a) = a ; aÎ[-p/2 ; p/2]

arcctg (ctg a) = a ; aÎ [ 0 ; p]

arcsin(sin a )=

1)a - 2pk; aÎ[-p/2 +2pk;p/2+2pk]

2) (2k+1)p - a; aÎ[p/2+2pk;3p/2+2pk]

arccos (cos a ) =

1) a-2pk ; aÎ[2pk;(2k+1)p]

2) 2pk-a ; aÎ[(2k-1)p; 2pk]

arctg(tg a )= a - p k

aÎ(-p/2 +pk;p/2+pk)

arcctg(ctg a ) = a - p k

aÎ(pk; (k+1)p)

arcsina = -arcsin (-a)= p/2-arccosa =

= arctg a/Ö(1-a?)

arccosa = p-arccos(-a)=p/2-arcsin a=

= arc ctga/Ö(1-a?)

arctga =-arctg(-a) = p/2 -arcctga =

= arcsin a/Ö(1+a?)

arc ctg a = p-arc cctg(-a) =

= arc cos a/Ö(1-a?)

arctg a = arc ctg1/a =

= arcsin a/Ö(1+a?)= arccos1/Ö(1+a?)

arcsin a + arccos = p/2

arcctg a + arctga = p/2

Тригонометрические уравнения

sin x = m ; |m| ? 1

x = (-1)ⁿ arcsin m + p k , kÎ Z

sin x =1 sin x = 0

x = p/2 + 2pk x = pk

sin x = -1

x = -p/2 + 2 pk

cos x = m ; |m| ? 1

x = ± arccos m + 2 p k

cos x = 1 cos x = 0

x = 2pk x = p/2+pk

cos x = -1

x = p+ 2pk

tg x = m

x = arctg m + pk

ctg x = m

x = arcctg m +pk

sin x/2 = 2t/(1+t² ); t - tg

cos x/2 = (1-t?)/(1+t?)

Показательные уравнения.

Неравенства: Если a^f(x) >(<) a^а(ч)

1) a>1, то знак не меняеться.

2) a<1, то знак меняется.

Логарифмы : неравенства:

log_a f(x) >(<) log _a j(x)

1. a>1, то : f(x) >0

j(x)>0

f(x)>j(x)

2. 0<a<1, то: f(x) >0

j(x)>0

f(x)<j(x)

3. log _f(x) j(x) = a

ОДЗ: j(x) > 0

f(x) >0

f(x ) ¹ 1

Тригонометрия:

1. Разложение на множители:

sin 2x - Ö3 cos x = 0

2sin x cos x -Ö3 cos x = 0

cos x(2 sin x - Ö3) = 0

....

2. Решения заменой ....

3.

sin? x - sin 2x + 3 cos? x =2

sin? x - 2 sin x cos x + 3 cos ? x = 2 sin? x + cos? x

Дальше пишеться если sin x = 0, то и cos x = 0,

а такое невозможно, => можно поделить на cos x

Тригонометрические нер-ва :

sin a ³ m

2 p k+ a ₁ ? a ? a ₂ + 2 p k

2 p k+ a ₂ ? a ? ( a ₁ +2 p )+ 2 p k

Пример:

I cos (p/8+x) < Ö3/2

pk+ 5p/6< p/8 +x< 7p/6 + 2pk

2pk+ 17p/24 < x< p/24+2pk;;;;

II sin a? 1/2

2pk +5p/6 ?a? 13p/6 + 2pk

cos a ³ ( ? ) m

2 p k + a ₁ < a < a ₂ +2 p k

2 p k+ a ₂ < a < ( a ₁ +2 p ) + 2 p k

cos a³ - Ö2/2

2pk+5p/4 ?a? 11p/4 +2pk

tg a ³ ( ? ) m

p k+ arctg m ? a ? arctg m + p k

ctg ³ ( ? ) m

p k+arcctg m < a < p + p k

Производная:

(xⁿ )^’ = n× x^n-1

(a^x )’ = a^x × ln a

(lg a^x )’= 1/(x×ln a)

(sin x)’ = cos x

(cos x)’ = -sin x

(tg x)’ = 1/cos? x

(ctg x)’ = - 1/sin?x

(arcsin x)’ = 1/ Ö(1-x?)

(arccos x)’ = - 1/ Ö(1-x?)

(arctg x)’ = 1/ Ö(1+x?)

(arcctg x)’ = - 1/ Ö(1+x?)

Св-ва:

(u × v)’ = u’×v + u×v’

(u/v)’ = (u’v - uv’)/ v?

Уравнение касательной к граф.

y = f(x₀ )+ f ’(x₀ )(x-x₀ )

уравнение к касательной к графику в точке x

1. Найти производную

2. Угловой коофициент k =

= производная в данной точке x

3. Подставим X₀ , f(x₀ ), f ‘ (x₀ ), выразим х

Интегралы :

ò xⁿ dx = xⁿ⁺¹ /(n+1) + c

ò a^x dx = ax/ln a + c

ò e^x dx = e^x + c

ò cos x dx = sin x + cos

ò sin x dx = - cos x + c

ò 1/x dx = ln|x| + c

ò 1/cos? x = tg x + c

ò 1/sin? x = - ctg x + c

ò 1/Ö(1-x?) dx = arcsin x +c

ò 1/Ö(1-x?) dx = - arccos x +c

ò 1/1+ x? dx = arctg x + c

ò 1/1+ x? dx = - arcctg x + c

Площадь криволенейной трапеции.

Геометрия

Треугольники

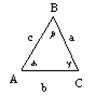
a + b + g =180

Теорема синусов

a? = b?+c? - 2bc cos a

b? = a?+c? - 2ac cos b

c? = a? + b? - 2ab cos g

Медиана дели треуг. на два равновеликих. Медиана делит

противопол. сторону напополам.

Биссектриса - угол.

Высота падает на пр. сторону

под прямым углом.

Формула Герона :

p=?(a+b+c)

_____________

S = Öp(p-a)(p-b)(p-c)

S = ?ab sin a

S_{равн .} =(a?Ö3)/4

S = bh/2

S=abc/4R

S=pr

Трапеция.

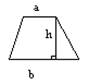
S = (a+b)/2× h

Круг

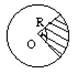
S= pR?

S_{сектора} =(pR?a)/360

Стереометрия

Параллепипед

V=S_осн ×Р

Прямоугольный

V=abc

Пирамида

V =1/3S_осн. ×H

S_полн. = S_бок. + S_осн.

Усеченная :

H . _____

V = 3 (S₁ +S₂ +ÖS₁ S₂ )

S₁ и S₂ — площадиосн.

S_{полн .} =S_{бок .} +S₁ +S₂

Конус

V=1/3 pR?H

S_{бок .} =pRl

S_{бок .} = pR(R+1)

Усеченный

S_бок. = pl(R₁ +R₂ )

V=1/3pH(R₁ ² +R₁ R₂ +R₂ ² )

Призма

V=S_осн. ×H

прямая: S_бок. =P_осн. ×H

S_полн. =S_бок +2S_осн.

наклонная :

S_бок. =P_пс ×a

V = S_пс ×a, а -бок. ребро.

P_пс — периметр

S_пс — пл. перпенд. сечения

Цилиндр.

V=pR?H ; S_бок. = 2pRH

S_полн. =2pR(H+R)

S_бок. = 2pRH

Сфера и шар .

V = 4/3 pR? - шар

S = 4pR? - сфера

Шаровой сектор

V = 2/3 pR?H

H - высота сегм.

Шаровой сегмент

V=pH?(R-H/3)

S=2pRH

град

0°

30°

45°

60°

90°

120°

135°

180°

a

-p/2

-p/3

-p/4

-p/6

0

p/6

p/4

p/3

p/2

2p/3

3p/4

3p/6

p

sina

-1

-Ö3/2

-Ö2/2

- ?

0

?

Ö2/2

Ö3/2

1

- ?

0

cosa

1

Ö3/2

Ö2/2

?

0

- ?

-Ö2/2

- Ö3/2

-1

tga

Ï

-Ö3

-1

-1/Ö3

0

1/Ö3

1

Ö3

Î

-Ö3

-1

0

ctga

---

Ö3

1

1/Ö3

0

-1/Ö3

-1

--

n	2	3	4	5	6	7	8	9
2	4	9	16	25	36	49	64	81
3	8	27	64	125	216	343	512	729
4	16	81	256	625	1296	2401	4096	6561
5	32	243	1024	3125	7776	16807	32768	59049
6	64	729	4096	15625	46656
7	128	2181
8	256	6561

-a	p-a	p+a	p/2-a	p/2+a	3p/2 - a	3p/2+a
sin	-sina	sina	-sina	cosa	cosa	-cosa	-cosa
cos	cosa	-cosa	-cosa	sina	-sina	-sina	sina
tg	-tga	-tga	tga	ctga	-ctga	ctga	-ctga
ctg	-ctga	-ctga	ctga	tga	-tga	tga	-tga