Referat.me
/ / Математический анализ. Регрессия

Название: Математический анализ. Регрессия

Вид работы: реферат

Рубрика: Математика

Размер файла: 181.7 Kb

Скачать файл: referat.me-216938.docx

Краткое описание работы: y=a уравнение регрессии. Таблица 1 1.35 1.09 6.46 3.15 5.80 7.20 8.07 8.12 8.97 10.66 Оценка значимости коэффициентов регрессии. Выдвигается и проверяется гипотеза о том что истинное значение коэффициента регрессии=0.

Математический анализ. Регрессия

y=a уравнение регрессии.

Таблица 1

x 1 2 3 4 5 6 7 8 9 10
y 1.35 1.09 6.46 3.15 5.80 7.20 8.07 8.12 8.97 10.66

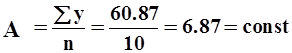
Оценка значимости коэффициентов регрессии.

Выдвигается и проверяется гипотеза о том что истинное значение коэффициента регрессии=0.

Для проверки гипотезы используется критерий Стьюдента.

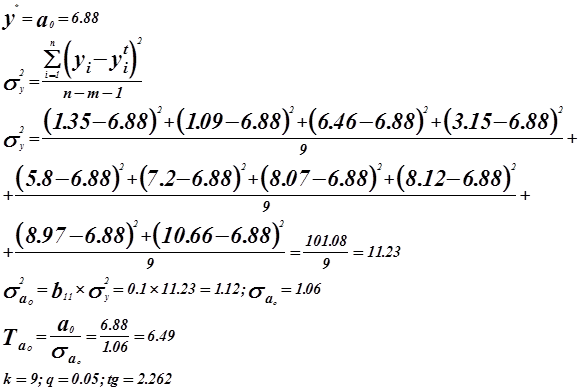
к-т является значимым и нулевую гипотезу отвергаем.

График 1

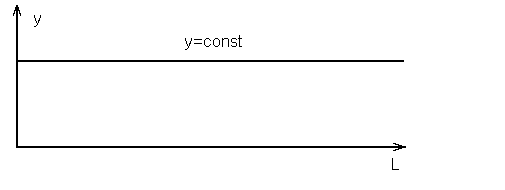
- уравнение регрессии

Таблица 2

x 1 2 3 4 5 6 7 8 9 10
y 1.35 1.09 6.46 3.15 5.80 7.20 8.07 8.12 8.97 10.66

Запишем матрицу X

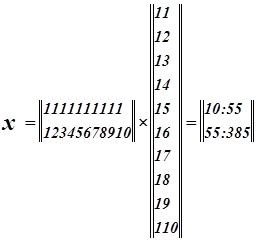
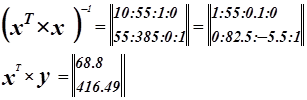
Система нормальных уравнений.

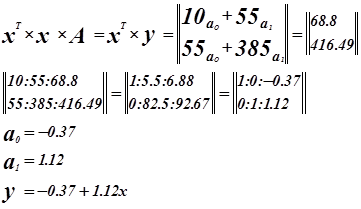
Оценка значимости коэффициентов регрессии.

Для проверки нулевой гипотезы используется критерий Стьюдента..

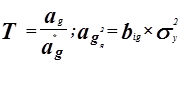
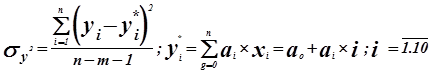
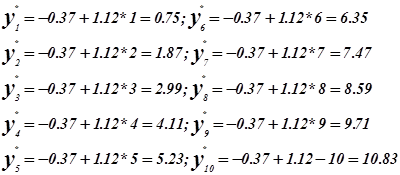
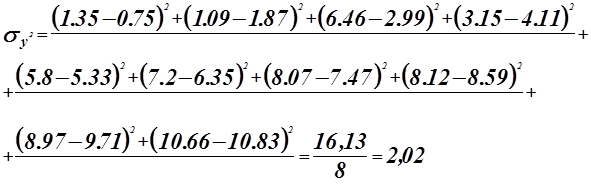
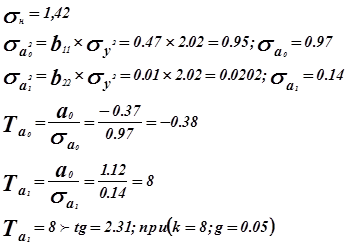
Коэффициент ai является значимости, т.к. не попал в интервал.

Проверка адекватности модели по критерию Фишера.

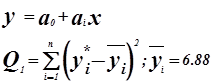
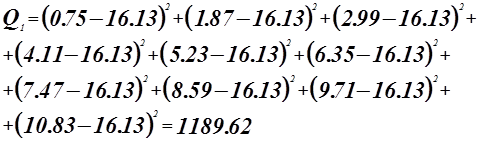
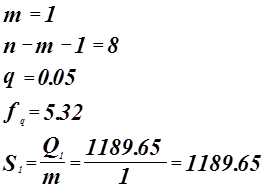
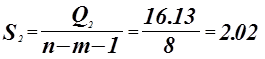
Критерий Фишера.

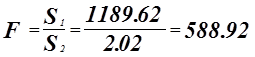
отсюда линия регрессии адекватна отраксает исходную информацию, гипотеза о равенстве мат. Ожиданий отвергается.

Проверка адекватности модели по коэффициенту детерминации или множественная корреляция.

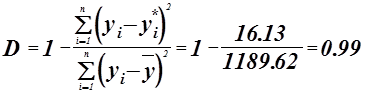
регрессионная модель адекватна

Коэффициент множественной корреляции:

Таблица 3

x 1 2 3 4 5 6 7 8 9 10
y 1.35 1.09 6.46 3.15 5.80 7.2 8.07 8.12 8.97 10.66

Приведем квадратное уравнение к линейной форме:

;

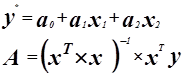
Запишем матрицу X.

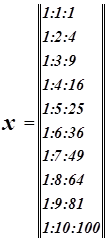
Составим матрицу Фишера.

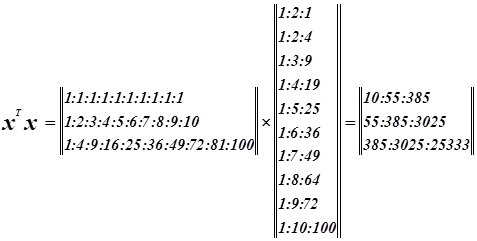
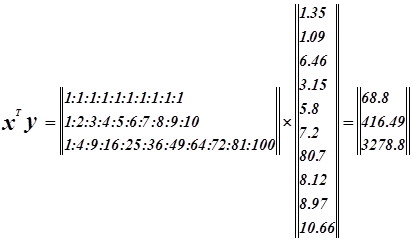
Система нормальных уравнений.

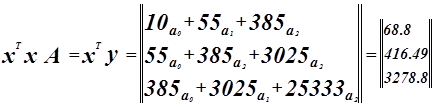
Решим ее методом Гаусса.

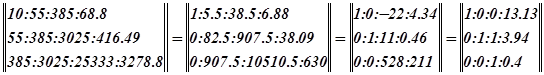
Уравнение регрессии имеет вид:

Оценка значимости коэффициентов регрессии.

Для проверки нулевой гипотезы используем критерий Стьюдента.

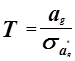
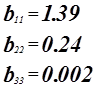
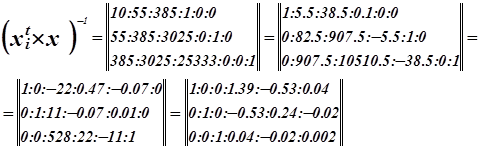
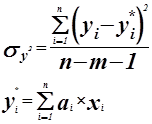
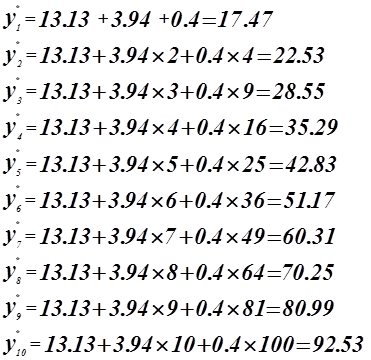
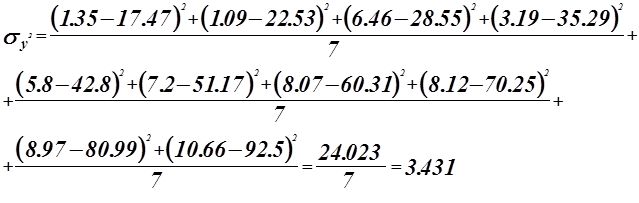
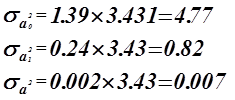
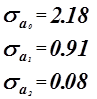
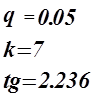
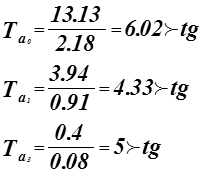
Коэффициенты значимые коэффициенты.

Проверка адекватности модели по критерию Фишера.

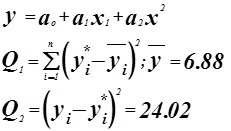
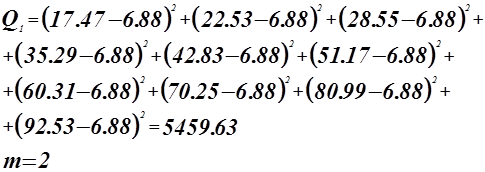
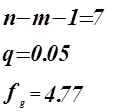
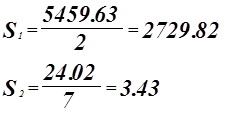
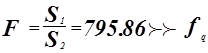гипотеза о равенстве математического ожидания отвергается.

Проверка адекватности модели по коэффициенту детерминации или множественной корреляции.

Коэффициент детерминации :

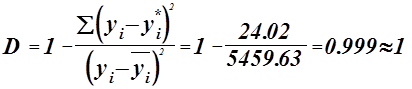
- регрессионная модель адекватна.

Коэффициент множественной корреляции

Таблица 4

x 1 2 3 4 5 6 7 8 9 10
y 0,75 1,87 2,99 4,11 5,23 6,35 7,47 8,59 9,71 10,83

График 2

Таблица 5

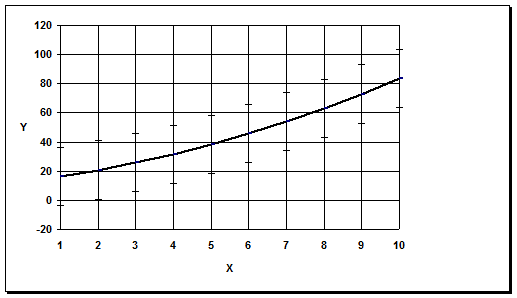
x 1 2 3 4 5 6 7 8 9 10
y 16.57 20.81 25.85 31.69 38.3 45.8 54 63.05 72.9 83.53

График 3

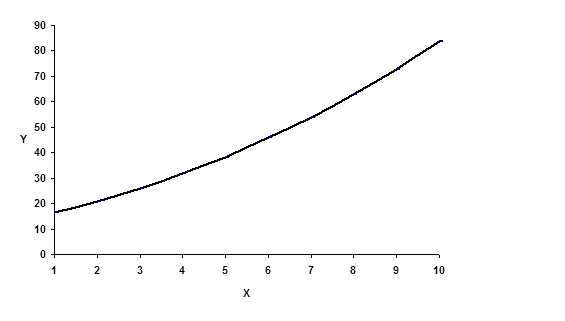
Использование регрессионной модели

для прогнозирования изменения показателя

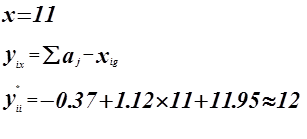
Оценка точности прогноза.

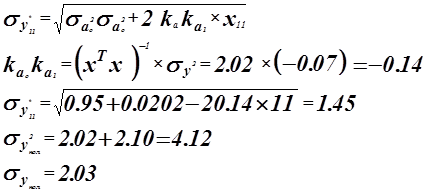
Построим доверительный интервал для заданного уровня надежности.

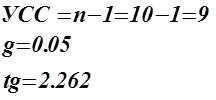
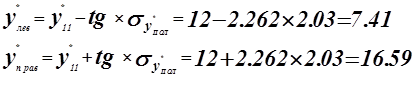
С вероятностью 0,05 этот интервал покрывает истинное значение прогноза

График 4

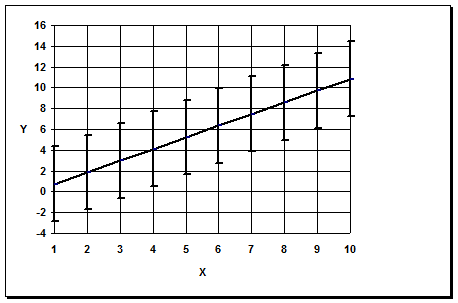
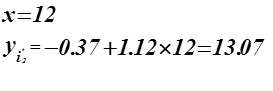
Оценка точности периода.

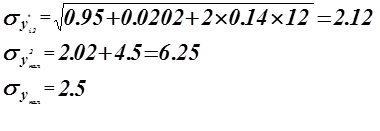
Построим доверительный интервал.

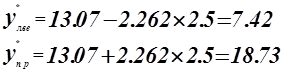
График 5

Похожие работы

  • Парная регрессия 3

    ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

  • Лабароторная работа по Эконометрике

    Министерство образования и науки Российской Федерации Федеральное агентство по образованию Филиал государственного образовательного учреждения высшего профессионального образования

  • Парная линейная регрессия

    Контрольная работа по эконометрике «Парная линейная регрессия» Вариант №6 В таблице приведены значения выручки от экспорта 1 тонны синтетического каучука за 10 кварталов и цены его на внутреннем рынке.

  • Контрольная работа по Эконометрике

    Построим поле корреляции (на отдельном листе) и сформулируем гипотезу о форме связи, предполагая, что генеральное уравнение регрессии – линейное: Найдем оценки b0 и b1 параметров модели парной линейной регрессии

  • Вычисление наибольшей прибыли предприятия

    Содержание Задача 1 Пусть х (млн. шт.) – объем производства, С(х)=2х3-7х и D(x)=2х2+9х+15 – соответственно функция издержек и доход некоторой фирмы. При каком значении х фирма получит наибольшую прибыль π(х)? какова эта прибыль?

  • Анализ накладных расходов

    Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования

  • по Экономико-математическому моделированию

    На основе данных выданных преподавателем необходимо: 1. Определить параметры следующих уравнений регрессии: а) линейного; б) гиперболического; в) степенного;

  • Зависимость цены от качества

    ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ КАФЕДРА МАТЕМАТИКИ И ИНФОРМАТИКИ ЛАБОРАТОРНАЯ РАБОТА по эконометрике Вариант № 1 Омск, 2010 г.

  • Определение зависимости цены товара

    ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ

  • Уравнения регрессии. Коэффициент эластичности, корреляции, детерминации и F-критерий Фишера

    Автономная некоммерческая организация Высшего профессионального образования «ПЕРМСКИЙ ИНСТИТУТ ЭКОНОМИКИ И ФИНАНСОВ» Факультет Экономический