Название: Нахождение оптимальных параметров для полета тела через прямоугольную преграду
Вид работы: реферат
Рубрика: Математика
Размер файла: 58.33 Kb
Скачать файл: referat.me-217393.docx
Краткое описание работы: Произвести необходимые расчеты для нахождения минимальной скорости тела, брошенного через прямоугольное препятствие.
Нахождение оптимальных параметров для полета тела через прямоугольную преграду
Выполнил: ученик 11 Б класса Назаркин Павел Дмитриевич
Муниципальное общеобразовательное учреждение «Лицей №43»
Саранск, 2004
Постановка задачи.
Произвести необходимые расчеты для нахождения минимальной скорости тела, брошенного через прямоугольное препятствие.
Методы выполнения работы.
Для выполнения данной работы проделаем ряд математических вычислений и преобразований с использованием физических формул.
Зная, что траекторией движения тела, является парабола, а также математическую формулу записи данной линии, будем использовать уравнение параболы общего вида в качестве начальных данных поставленной задачи. В выбранной нами прямоугольной системе координат запишем данное уравнение для двух точек, принадлежащих линии движения – начальной точке А и точке В, в которой тело окажется через некоторый промежуток времени t. Решая систему полученных при этом уравнений, путем математических замен и преобразований выведем формулу зависимости движения тела от одной переменной L, т.е. коэффициенты k и b, участвующие в общем виде уравнения параболы, выразим через L. Затем, используя физический закон движения тела, брошенного под углом к горизонту, выразим переменную L через ![]() и V . В результате получим уравнение движения, в качестве коэффициентов в котором будут выступать переменные
и V . В результате получим уравнение движения, в качестве коэффициентов в котором будут выступать переменные ![]() и V. Затем составим систему двух уравнений, полученных подстановкой координат точек А и В в последнее уравнение движения. Решая данную систему, мы найдем неизвестные нам величины
и V. Затем составим систему двух уравнений, полученных подстановкой координат точек А и В в последнее уравнение движения. Решая данную систему, мы найдем неизвестные нам величины ![]() и V, выразив их через имеющиеся известные нам параметры – ширину и высоту прямоугольного препятствия. Для нахождения Vmin воспользуемся производной функции.
и V, выразив их через имеющиеся известные нам параметры – ширину и высоту прямоугольного препятствия. Для нахождения Vmin воспользуемся производной функции.
Решение.
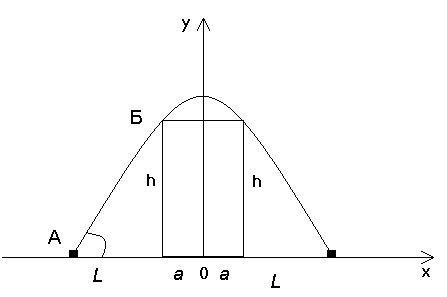
Уравнением линии движения тела, брошенного через прямоугольное препятствие, в общем виде является уравнение параболы :
y=-kx2+b
Введем прямоугольную систему координат и свяжем ее с прямоугольным препятствием, как показано на рисунке.
В данной системе координат уравнение движения тела в точках А и Б примет вид:
![]() 0=-k(a+L)2+b,
0=-k(a+L)2+b,
h=-ka2+b.
Выразим k и b через одну неизвестную L:
Вычитаем 1)-ое из 2)-ого:
h=k(a2+2aL+L2-a2),
h=k(2aL+L2) ,![]() (*);
(*);
![]()
![]() h=b-ka2+b b=h+ka2
h=b-ka2+b b=h+ka2 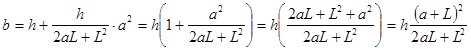 . (*)
. (*)
Получилось, что уравнение движения зависит только от L:
y=-kx2+b, где коэффициенты k и b имеют вид (*).
Найдем зависимость L от![]() и V.
и V.
Из курса физики известно: что движение тела, брошенного под углом горизонта описывается уравнениями
![]()
![]()
![]() x=Vxt L=Vxt L=Vcos
x=Vxt L=Vxt L=Vcos![]() t
t
![]()
![]() y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
gt2-2Vyt+2h=0.
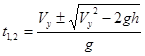 .
.
Мы рассматриваем время движения от точки А до Б, значит
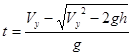 , где Vy=Vsin
, где Vy=Vsin![]() .
.
Итак, 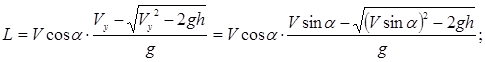
Умножив обе части уравнения на g, получим:
![]() (1)
(1)
Известно, что 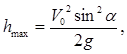 т.е.
т.е. ![]()
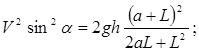 (2)
(2)
С другой стороны tg![]() =y’ в точке А, т.е. tg
=y’ в точке А, т.е. tg![]() =y’(-a-L);
=y’(-a-L);
![]()
Подставив значение tg![]() в (2), получим:
в (2), получим:
V2sin2![]() =g(a+L) tg
=g(a+L) tg ![]()
![]()
![]() V2sin
V2sin![]() cos
cos![]() =g(a+L) Lg=V2sin
=g(a+L) Lg=V2sin![]() cos
cos![]() -ga (3)
-ga (3)
Сравнив (1) и (3) получаем, что:
![]()
![]() .
.
Получили уравнение с двумя неизвестными V и![]() : выразив V через
: выразив V через ![]() , мы получим ту самую функцию, которую мы должны были найти:
, мы получим ту самую функцию, которую мы должны были найти:
Пусть z=V2, тогда z cos2![]() (z sin2
(z sin2![]() -2gh)=g2a2;
-2gh)=g2a2;
z2 cos2![]() sin2
sin2![]() - z cos2
- z cos2![]() 2gh-g2a2=0;
2gh-g2a2=0;
Получили квадратное уравнение относительно z
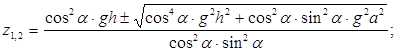
Очевидно, ![]() значит, т.к. z=V2>0, то
значит, т.к. z=V2>0, то 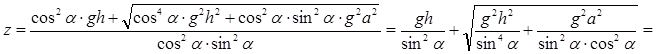
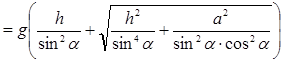 .
.
Вместо зависимости V от ![]() рассмотрим зависимость z от
рассмотрим зависимость z от ![]() , и обозначив
, и обозначив ![]() получим зависимость z от t.
получим зависимость z от t.
Получим ![]() , где z=V2,
, где z=V2, ![]() .
.
Выразим ![]() через t, если
через t, если ![]() ;
; ![]()
![]()
Значит, ![]()
Т.е. 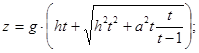
![]()
Таким образом, чтобы найти Vmin и ![]() , нам нужно во-первых, найти fmin и t.
, нам нужно во-первых, найти fmin и t.
![]()
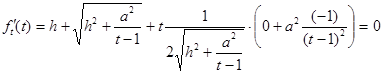 .
.
Умножив обе части уравнения на ![]() , получим
, получим
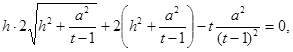
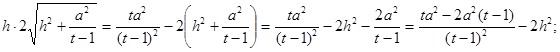
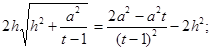
Прежде чем возвести обе части в квадрат, сделаем предварительный анализ получившегося уравнения: т.к. ![]()
то и ![]()
т.е. ![]() и
и ![]()
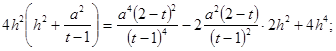
![]()
![]()
![]()
Умножив обе части уравнения на (t-1)2, получим
![]()
![]()
![]() Т.к t<2 и t>1 (т.к.
Т.к t<2 и t>1 (т.к. ![]() ), то можно извлечь корень.
), то можно извлечь корень.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ; (4)
; (4)
![]()
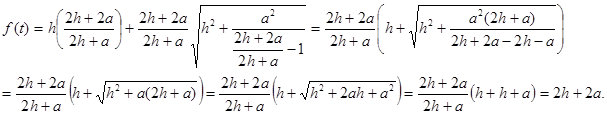
 Итак, f(t)=2h+2a, значит
Итак, f(t)=2h+2a, значит ![]() .
.
Т.к. z=V2, то ![]() т.е.
т.е. ![]() (5)
(5)
Осталось найти L:
Его найдем используя (3).
![]()
![]()

![]()
![]()

![]()
![]()
Результаты работы.
Проделанным расчетом мы нашли зависимость скорости, движения брошенного через прямоугольное препятствие тела, так чтобы она была минимальной, от длины и высоты прямоугольного препятствия. То есть, зная данные препятствия, - его длину и ширину – а так же формулы, полученные в данной работе, мы можем определить на каком расстоянии от препятствия, под каким углом и с какой минимальной скоростью необходимо бросить тело, чтобы оно перелетело через это препятствие.
Актуальность темы.
Данные расчеты и выведенные формулы используются в различных сферах деятельности человека. В частности, в военной практике, для правильного расчета движения траектории снарядов.
Приложение.
К работе прилагается программа, результатом которой является вывод на экран траектории движения тела, брошенного через прямоугольное препятствие. Входными параметрами программы являются данные прямоугольного препятствия – его длина и высота. Программа написана на языке программирования Delphi.
Похожие работы
-
Основы теории относительности
Важнейшими постулатами классической механики, основы которой были заложены Галилеем и Ньютоном, являются принцип изотропности и однородности пространства и времени, три закона Ньютона, а также закон сложения скоростей Галилея.
-
Метеоры
Метеорные тела — остатки комет, видимые лишь в момент испарения, называются метеорами. Ширина метеорных потоков неизмеримо больше, чем размер породивших их ядер.
-
Механика
Основные сведения о кинематике, динамика поступательного и вращательного движения.
-
Математическое моделирование
Математическое моделирование экономических параметров: определение вида и параметров функций спроса, затрат и производственной функции выпуска.
-
Экзаменационные билеты по теоретической механике
Билеты по разделу "Динамика".
-
Элементы специальной теории относительности
В своей работе «К электродинамике движущихся тел», опубликованной в 1905г., Эйнштейн сформулировал более точную теорию механики быстродвижущихся тел - специальную теорию относительности.
-
Бредли против Лоренца
Астрономы давно заметили, что при годовом движении Земли по орбите звёзды описывают эллипсы. Это явление назвали звёздной аберрацией.
-
Интегралы, объем тела вращения, метод наименьших квадратов
Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.
-
Галилей и законы движения
Из всего, что происходит в окружающем мире, наибольший интерес Галилея вызывали разнообразные движения. Он по крупицам собирает все, что написано о движении у древних.
-
Баллистика и баллистическое движение
Основы баллистики и баллистического движения. История возникновения баллистики. Основные термины. Скорость при баллистическом движении. Траектория движения тела в поле тяжести. Траектория баллистического движения.