Referat.me
/ / Интегралы, объем тела вращения, метод наименьших квадратов

Название: Интегралы, объем тела вращения, метод наименьших квадратов

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 34.3 Kb

Скачать файл: referat.me-215645.docx

Краткое описание работы: Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.

Интегралы, объем тела вращения, метод наименьших квадратов

Контрольная работа (вариант 8)

1. Найти неопределенные интегралы:

2. Интегрирование по частям

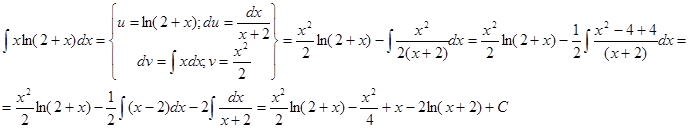
Вычислить определенные интегралы:

3.

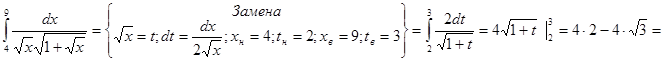
=8-6,92=1,08

Интегрирование по частям

4.

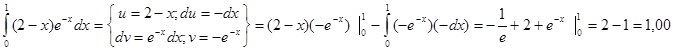
5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями

. Построить чертеж.

Решение.

В декартовой системе координат построим линии и найдем точки их пересечения.

Объем тела вращения по формуле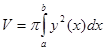

Точки пересечения линий

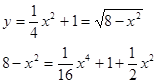
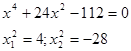
(второй вариант не подходит, т.к. отрицателен)

Отсюда

Границы фигуры:

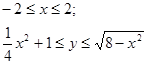
Фигура симметрична относительно оси ОУ, поэтому

Объем тела


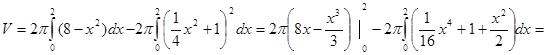
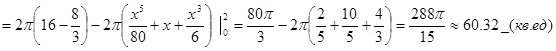
6. Методом наименьших квадратов найти эмпирическую формулу вида y=ax+b для функции, заданной следующей таблицей:

X

3.3

3.5

3.7

3.9

4.1

Y

13

13.5

11.4

11.2

9.7

Изобразить графически таблично заданную и соответствующую линейную функции. По эмпирической формуле вычислить значение переменной при х=4,0

Решение

Заполним таблицу

2

1

3,3

13

10,89

42,9

2

3,5

13,5

12,25

47,25

3

3,7

11,4

13,69

42,18

4

3,9

11,2

15,21

43,68

5

4,1

9,7

16,81

39,77

S

18,5

58,8

68,85

215,78

Составим для определения коэффициентов систему уравнений вида:

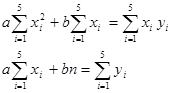
Получим

Решая систему методом исключения определяем:

Искомая эмпирическая формула y=28.23-4.45x

Значение переменной при x=4.0

y=28.23-4.45*4=10.43

7. Исследовать сходимость ряда.

Исследуем ряд сначала на абсолютную сходимость. Общий член ряда

В свою очередь ряд расходится как гармонический. Значит абсолютной сходимости у исходного ряда нет. Исследуем на условную сходимость по признаку Лейбница.

1) при


2)

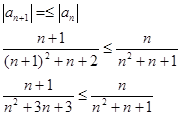
действительно для

По признаку Лейбница, исходный ряд сходится условно.

Похожие работы

  • Вычисление интегралов

    Методика и основные этапы нахождения параметров: площади криволинейной трапеции и сектора, длины дуги кривой, объема тел, площади поверхности тел вращения, работы переменной силы. Порядок и механизм вычисления интегралов с помощью пакета MathCAD.

  • Математический анализ

    Исследование заданной функции и построение ее графика. Расчет объема тела, полученного вращением вокруг оси абсцисс фигуры, ограниченной линиями и осями координат. Вычисление интеграла при заданной силе. Работа, которую нужно совершить для сжатия пружины.

  • Формулы по математическому анализу

    Формулы дифференцирования Таблица основных интегралов Правила интегрирования Основные правила дифференцирования Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

  • Определенный интеграл

    Определенный интеграл Содержание Лекция 1. Определенный интеграл 1. Понятие определенного интеграла 2. Геометрический смысл определенного интеграла

  • Система уравнений по формулам Крамера

    Задание № 1 Решить систему уравнений: 1) по формулам Крамера 2) с помощью обратной матрицы 3) методом Гаусса Решение найдем определитель матрицы 1) методом Крамера

  • Решение дифференциальных уравнений

    Задачи на нахождение неопределенного интеграла с применением метода интегрирования по частям. Вычисление площади, ограниченной заданными параболами. Решение дифференциального уравнения первого порядка. Исследование на сходимость ряда; признаки сходимости.

  • Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых)

    Лабораторная работа № 4. Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых). Гребенникова Марина 12-А класс Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

  • Билеты по математическому анализу

    Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № Сформулируйте понятие полного дифференциала функции двух переменных и объясните его геометрический смысл.

  • Интегралы. Функции переменных

    Метод интегрирования по частям. Задача на нахождение частных производных 1-го порядка. Исследование на экстремум заданную функцию. Нахождение частных производных. Неоднородное линейное дифференциальное уравнение 2-го порядка. Условия признака Лейбница.

  • Геометрические и физические приложения двойных, тройных, криволинейных и поверхностных интеграло

    СОДЕРЖАНИЕ 1.Геометрические приложения интегралов 1.1 Геометрические приложения двойных интегралов………….. 3 1.2 Геометрические приложения тройных интегралов………….. 5