Название: Разностные аппроксимации
Вид работы: реферат
Рубрика: Математика
Размер файла: 217.1 Kb
Скачать файл: referat.me-217519.docx
Краткое описание работы: Примеры разностных аппроксимаций. Исследование аппроксимации и сходимости. Разностные схемы для уравнения теплопроводности.
Разностные аппроксимации
1. Примеры разностных аппроксимаций.
Различные способы приближенной замены одномерных дифференциальных уравнений разностными изучались ранее. Напомним примеры разностных аппроксимаций и введем необходимые обозначения. Будем рассматривать равномерную сетку с шагом h , т.е. множество точек
w h ={xi =ih, i=0, ± 1, ± 2,…}.
![]() Пусть u(x)
– достаточно гладкая функция, заданная на отрезке [xi-1
, xi+1
]. Обозначим
Пусть u(x)
– достаточно гладкая функция, заданная на отрезке [xi-1
, xi+1
]. Обозначим
Разностные отношения
называются соответственно правой, левой и центральной разностными производными функции u(x) в точке xi , т.е. при фиксированном xi и при h®0 (тем самым при i®¥) пределом этих отношений является u’(xi ) . Проводя разложение по формуле Тейлора, получим
ux,i – u’(xi ) = 0,5hu’’(xi ) + O(h2 ),
ux,i – u’(xi ) = -0,5hu’’(xi ) + O(h2 ),
ux,i – u’(xi ) = O(h2 ),
Отсюда видно, что левая и правая разностные производные аппроксимируют u’(x) с первым порядком по h , а центральная разностная производная – со вторым порядком. Нетрудно показать, что вторая разностная производная
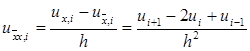 |
аппроксимирует u’’(xi ) со вторым порядком по h , причем справедливо разложение
Рассмотрим дифференциальное выражение
(1)
с переменным коэффициентом k(x) . Заменим выражение (1) разностным отношением
(2)
где a=a(x) – функция, определенная на сетке wh . Найдем условия, которым должна удовлетворять функция a(x) для того, чтобы отношение (aux )x,i аппроксимировало (ku’)’ в точке xi со вторым порядком по h . Подставляя в (2) разложения
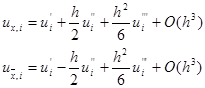 |
где ui ’ = u’(xi ) , получим
С другой стороны, Lu = (ku’)’ = ku’’ + k’u’,
т.е.
Отсюда видно, что Lh u–Lu = O(h2 ) , если выполнены условия
(3)
Условия (3) называются достаточными условиями второго порядка аппроксимации . При их выводе предполагалось, что функция u(x) имеет непрерывную четвертую производную и k(x) – дифференцируемая функция. Нетрудно показать, что условиям (3) удовлетворяют, например, следующие функции:
Заметим, что если положить ai = k(xi ), то получим только первый порядок аппроксимации.
В качестве следующего примера рассмотрим разностную аппроксимацию оператора Лапласа
(4)
Введем на плоскости (x1 , x2 ) прямоугольную сетку с шагом h1 по направлению x1 и с шагом h2 по направлению x2 , т.е. множество точек
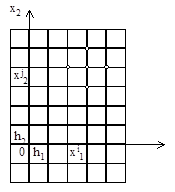 w
h
= {(xi
1
, xj
2
) | xi
1
= ih1
, xj
2
= jh2
; i, j = 0,
±
1,
±
2,…},
w
h
= {(xi
1
, xj
2
) | xi
1
= ih1
, xj
2
= jh2
; i, j = 0,
±
1,
±
2,…},
и обозначим
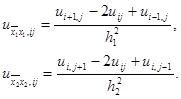 |
Из предыдущих рассуждений следует, что разностное выражение
(5)
аппроксимирует дифференциальное выражение (4) со вторым порядком, т.е. Lh uij – Lu(xi 1 , xj 2 ) = O(h2 1 ) + O(h2 2 ). Более того, для функций u(x1 , x2 ), обладающих непрерывными шестыми производными, справедливо разложение
Разностное выражение (5) называется пятиточечным разностным оператором Лапласа , так как оно содержит значения функции u(x1 , x2 ) в пяти точках сетки, а именно в точках (x1 i , x2 j ), (x1 i ± 1 , x2 j ), (x1 i , x2 j ± 1 ). Указанное множество точек называется шаблоном разностного оператора. Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих большее число точек.
2. Исследование аппроксимации и сходимости
2.1. Аппроксимация дифференциального уравнения. Ранее рассматривалась краевая задача
(k(x) u’(x))’ – q(x) u(x) + f(x) = 0, 0 < x < l, (1)
– k(0) u’(0) + b u(0) = m 1 , u(l) = m 2 , (2)
k(x) ³ c1 > 0, b ³ 0,
для которой интегро-интерполяционным методом была построена разностная схема
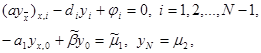 |
(3)
(4)
где
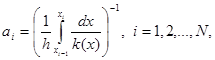 |
(5)
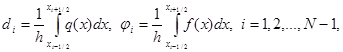 |
(6)
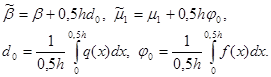 |
Обозначим через Lu(x) левую часть уравнения (1) и через Lh yi – левую часть уравнения (3), т.е.
Пусть u (x) – достаточно гладкая функция и u (xi ) – ее значение в точке xi сетки
w h = {xi = ih, i = 0, 1, …,N, hN = l} (7)
Говорят, что разностный оператор Lh аппроксимирует дифференциальный оператор L в точке x=xi , если разность Lh u i – Lh u (xi ) стремится к нулю при h®0. В этом случае говорят также, что разностное уравнение (3) аппроксимирует дифференциальное уравнение (1).
Чтобы установить наличие аппроксимации, достаточно разложить по формуле Тейлора в точке x=xi значения u i ± 1 = u (xi ± h) , входящие в разностное выражение Lh u i . Большая часть этой работы проделана в предыдущей главе, где показано, что при условиях
![]() (8)
(8)
выполняется соотношение
Если кроме того, докажем, что
di = q(xi ) + O(h2 ), j i = f(xi ) + O(h2 ) (9)
то тем самым будет установлено, что оператор Lh аппроксимирует L со вторым порядком по h , т.е.
Lh u i – L u (xi ) = O(h2 ), i = 1, 2,…, N–1 (10)
Итак, доказательство второго порядка аппроксимации сводится к проверке сводится к проверке условий (8), (9) для коэффициентов (5), (6). Проверим сначала выполнение условий (8). Обозначая p(x) = k-1 (x) , получим
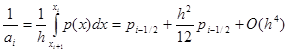 |
следовательно,
Аналогично
Отсюда получим
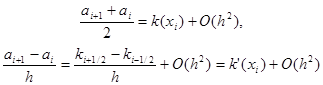 |
т.е. условия (8) выполнены. Условия (9) выполнены в силу того, что замена интегралов (6) значениями qi , fi соответствует приближенному вычислению этих интегралов по формуле прямоугольников с узлом в середине отрезка интегрирования.
2.2. Аппроксимация граничного условия. Исследуем погрешность аппроксимации разностного граничного условия (4). Обозначим lh u (0) = –a1 u x, 0 + b u 0 . Если u (x) – произвольная достаточно гладкая функция, то очевидно
lh u (0) = –k(0) u ’(0) + b u (0) + O(h) ,
т.е. имеет место аппроксимация первого порядка по h . Однако если u =u(x) – решение задачи (1), (2), то разностное граничное условие (4) имеет второй порядок аппроксимации, т.е.
Докажем последнее утверждение. Используя разложение
ux, 0 = (u1 – u0 )/h = u’(x1/2 ) + O(h2 ), x1/2 = 0,5h,
a1 = k1/2 + O(h2 )
получим
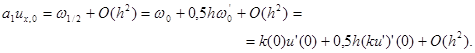 |
Отсюда имеем
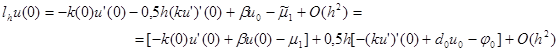 |
Учитывая граничное условие (2), получаем
lh u(0) = 0,5h [– (ku’)’(0) + d0 u0 – j 0 ] + O(h2 ) .
Выражение, стоящее в квадратных скобках, преобразуем, учитывая уравнение (1), к виду
– (ku’)’(0) + d0 u0 – j 0 = – (ku’)’(0) + q(0)u(0) – f(0) +
+ (d0 – q(0))u0 – (f(0) – j 0 ) = (d0 – q(0))u0 – (f(0) – j 0 ) .
Из соотношений
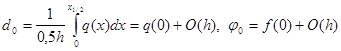 |
получаем
что и требовалось доказать.
Таким образом, при достаточной гладкости коэффициентов k(x), q(x), f(x) и решения u(x) разностная схема (10) аппроксимирует исходную задачу (2) со вторым порядком по h .
При практическом использовании разностной схемы для нахождения ее коэффициентов не обязательно вычислять интегралы (4), (6) точно. Можно воспользоваться коэффициентами, полученными путем замены этих интегралов квадратурными формулами, имеющими точность O(h2 ) и выше. Например, в результате применения формулы прямоугольников получим следующие коэффициенты: ai = k(xi – 0,5h), di = q(xi ), j i = f(xi ).
Применяя формулу трапеций, получим
Представление коэффициентов разностной схемы в виде интегралов (4), (6) оказывается полезным при исследовании сходимости в случае разрывных функций k(x), q(x), f(x) .
2.3. Уравнение для погрешности. Решение yi = y(xi ) разностной задачи (3), (4) зависит от шага h сетки, y(xi ) = yh (xi ) . По существу, мы имеем семейство решений {yh (xi )} , зависящее от параметра h . Говорят, что решение yh (x) разностной задачи сходится к решению u(x) исходной дифференциальной задачи, если при h®0 погрешность yh (xi ) – u(xi ), i = 0, 1,…, N , стремится к нулю в некоторой норме. В настоящем параграфе в качестве такой нормы будем брать норму в сеточном пространстве C( w h ) , т.е. положим
Говорят, что разностная схема имеет m-й порядок точности (или сходится с порядком m ), если
где m>0, M>0 – константы, не зависящие от h .
Выше было установлено, что схема (3), (4) имеет второй порядок аппроксимации. Докажем теперь, что эта схема имеет и второй порядок точности. Для этого прежде всего выпишем уравнение, которому удовлетворяет погрешность zi = yi – u(xi ) . Поставим yi = zi + u(xi ) в уравнения (3), (4). Тогда получим уравнения
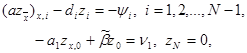 (11)
(11)
(12)
где обозначено
Функция y i , входящая в правую часть уравнения (11), называется погрешностью аппроксимации дифференциального уравнения (1) разностным уравнением (3) на решении задачи (1), (2). В п.1 было доказано, что y i = O(h2 ) при h®0, i=1, 2,…, N–1 . Аналогично, величина n1 является по определению погрешностью аппроксимации краевого условия (2) разностным краевым условием (4) на решении задачи (1), (2), причем n 1 =O(h2 ) . Таким образом, структура уравнений для погрешности (11), (12) та же, что и у разностной схемы (3), (4), отличаются только правые части.
Чтобы доказать сходимость разностной схемы, оценим решение задачи (11), (12) через правые части y i , n 1 , т.е. получим неравенство вида
![]() (13)
(13)
![]() с константой M1
, не зависящей от h
. Из этого неравенства и будет следовать, что
с константой M1
, не зависящей от h
. Из этого неравенства и будет следовать, что
Отметим, что неравенства вида (13), называемые априорными оценками, нашли широкое применение в теории разностных схем. Поскольку структура для погрешности (11), (12) та же, что и у разностной схемы (3), (4), а отличаются только правые части, то оценка (13) выполняется одновременно с аналогичной оценкой
для разностной схемы (3), (4) при m 2 = 0 . Последняя оценка выражает устойчивость решения разностной задачи по правым частям j и m 1 .
2.4. Разностные тождества и неравенства. Для того, чтобы доказать неравенство (13), нам потребуются некоторые разностные тождества и неравенства. Будем рассматривать сеточные функции, заданные на сетке (7). Обозначим
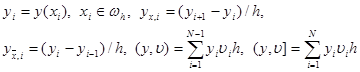 |
Справедливо следующее разностное утверждение:
(y, u x ) = –( u , yx ) + yN u N – y0 u 1 . (14)
Действительно,
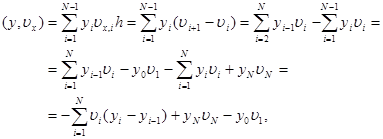 |
что и требовалось доказать. Тождество (14) называется формулой суммирования по частям .
Подставляя в (14) вместо u выражение azx и вместо y функцию z, получаем первую разностную формулу Грина
(15)
![]() Здесь В частности, если zN
= 0
(как в задаче (11), (12)), то получим
Здесь В частности, если zN
= 0
(как в задаче (11), (12)), то получим
(16)
Обозначим
и докажем, что для любой сеточной функции zi , удовлетворяющей условию zN = 0 , справедливо неравенство
(17)
Для доказательства воспользуемся тождеством
и применим неравенство Коши-Буняковского
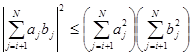 |
Тогда получим
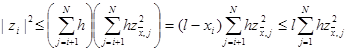 |
Откуда сразу следует неравенство (17).
2.5. Доказательство сходимости. Возвращаясь к доказательству сходимости схемы (3), (4), получим тождество, которому удовлетворяет погрешность zi = yi – u(xi ) . Для этого умножим уравнение (11) на hzi и просуммируем по i от 1 до N–1 . Тогда получим
Отсюда, применяя разностную формулу Грина (16), получим
Далее, согласно (12) имеем
следовательно, справедливо тождество
(18)
Из этого тождества и будет сейчас выведено требуемое неравенство вида (13).
Заметим прежде всего, что если
k(x) ³ c1 > 0, b ³ 0, q(x) ³ 0,
то коэффициенты разностной схемы (3), (4) удовлетворяют неравенствам
ai ³ c1 > 0, b ³ 0, di ³ 0. (19)
Это утверждение сразу следует из явного представления коэффициентов (5), (6).
Воспользовавшись (19), оценим слагаемые, входящие в левую часть тождества (18), следующим образом:
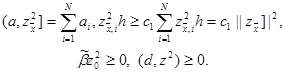 |
Тогда придем к неравенству
![]() (20)
(20)
Оценим сверху правую часть этого неравенства. Будем иметь
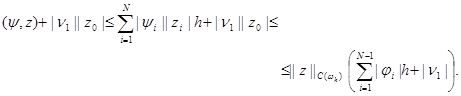 |
Подставляя эту оценку в (20) и учитывая неравенство (17), получим
т.е.
Окончательно
(21)
Поскольку из неравенства следует,
что погрешность zi = yi – u(xi ) также является величиной O(h2 ) при h®0. Итак, справедливо следующее утверждение.
Пусть k(x) – непрерывно дифференцируемая и q(x), f(x) – непрерывные функции при x Î [0, l], решение u(x) задачи (1), (2) обладает непрерывными четвертыми производными. Пусть коэффициенты разностной схемы (3), (4) удовлетворяют условиям (8), (9), (19). Тогда решение разностной задачи (3), (4) сходится при h ® 0 к решению исходной дифференциальной задачи (1), (2) со вторым порядком по h, так что выполняется оценка
где M – постоянная, не зависящая от h.
3. Разностные схемы для уравнения теплопроводности
3.1. Исходная задача. Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области {0 < x < 1, 0 < t £ T} требуется найти решение уравнения
(1)
удовлетворяющее начальному условию
u(x, 0) = u0 (x) (2)
и граничным условиям
u(0, t) = m 1 (t), u(1, t) = m 2 (t). (3)
Здесь u0(x), m 1 (t), m 2 (t) – заданные функции. Известно, что при определенных предположениях гладкости решение задачи (1)–(3) существует и единственно. В дальнейшем при исследовании аппроксимации разностных схем будем предполагать, что решение u(x, t) обладает необходимым по ходу изложения числом производных по x и по t. Решение задачи (1) – (3) удовлетворяет принципу максимума и тем самым непрерывно зависит от начальных и граничных данных.
3.2. Явная схема. Как всегда, для построения разностной схемы надо прежде всего ввести сетку в области изменения независимых переменных и задать шаблон, т.е. множество точек сетки, участвующих в аппроксимации дифференциального выражения. Введем сетку по переменному x такую же, как в предыдущей главе, т.е.
w h = {xi = ih, i = 0, 1,…, N, hN = 1}
и сетку по переменному t с шагом t, которую обозначим
w t = {tn = n t , n = 0, 1,…, K, K t = T}
Точки (xi , tn ), i = 0, 1,…, N, n = 0, 1,…, K , образуют узлы пространственно-временной сетки wh, t = wh x wt . Узлы (xi , tn ) , принадлежащие отрезкам I0 = {0 £ x £ 1, t = 0}, I1 = {x = 0, 0 £ t £ T}, I2 = {x = 1, 0 £ t £ T} , называются граничными узлами сетки wh, t , а остальные узлы – внутренними. На рисунке граничные узлы обозначены крестиками, а внутренние – кружочками.
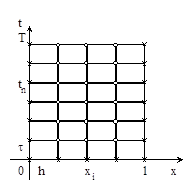 Слоем
называется множество всех узлов сетки wh,
t
, имеющих одну и ту же временную координату. Так, n-м слоем называется множество узлов
Слоем
называется множество всех узлов сетки wh,
t
, имеющих одну и ту же временную координату. Так, n-м слоем называется множество узлов
(x0 , tn ), (x1 , tn ),…, (xN , tn ) .
Для функции y(x, t) , определенной на сетке wh, t , введем обозначения yn i = y(xi , tn ) ,
(4)
Иногда для упрощения записи индексы i и n будем опускать, обозначая
![]()
( xi , tn+1 ) (xi-1 , tn+1 ) (xi , tn+1 ) (xi+1 , tn+1 )
 |
 |
(xi-1 , tn ) (xi , tn ) (xi+1 , tn ) (xi , tn )
(xi-1 , tn+1 ) (xi , tn+1 ) (xi+1 , tn+1 ) (xi , tn+1 )
 |
 |
(xi-1 , tn ) (xi , tn ) (xi+1 , tn ) (xi-1 , tn ) (xi , tn ) (xi+1 , tn )
(xi , tn-1 )
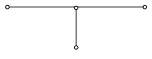
Чтобы аппроксимировать уравнение (1) в точке (xi , tn ), введем шаблон, изображенный на рисунке и состоящий из четырех узлов (xi ± 1 , tn ), (xi , tn ), (xi , tn+1 ). Производную ¶u/¶t заменим в точке (xi , tn ) разностным отношением yn t, i , а производную ¶2 u/¶2 x – второй разностной производной yn xx, i . Правую часть f(x, t) заменим приближенно сеточной функцией jn i , в качестве jn i можно взять одно из следующих выражений:
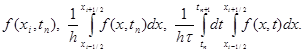 |
В результате получим разносное уравнение
(5)
которое аппроксимирует исходное дифференциальное уравнение в точке (xi , tn ) с первым порядком по t и вторым порядком по h при условии, что разность j n i – f(xi , tn ) имеет тот же порядок малости.
Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные (начальные и граничные) условия – в граничных узлах сетки. Разностную схему по аналогии с дифференциальной задачей будем называть также разностной задачей. В данном случае разностная схема имеет вид
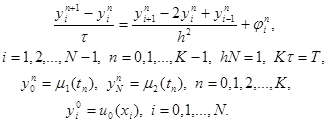 |
(6)
Эта схема представляет собой систему линейных алгебраических уравнений с числом уравнений, равным числу неизвестных. Находить решение такой системы следует по слоям. Решение на нулевом слое задано начальными условиями y0 i = u0 (xi ), i = 0, 1,…, N . Если решение yn i , i = 0, 1,…, N , на слое n уже найдено, то решение yi n+1 на слое n+1 находится по явной формуле
(7)
![]() а значения доопределяются изграничных
а значения доопределяются изграничных
условий. По этой причине схема (6) называется явной разностной схемой. Несколько позже мы познакомимся и с неявными схемами, в которых для нахождения yi n+1 при заданных yi n требуется решать систему уравнений.
Погрешность разностной схемы (6) определяется как разность zi n = yi n – u(xi , tn ) между решением задачи (6) и решением исходной задачи (1) – (3). Подставляя в (6) yi n = zi n + u(xi , tn ) , получим уравнение для погрешности
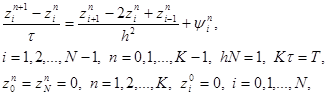 |
(8)
где – погрешность аппроксимации разностной
схемы (6) на решении задачи (1) – (3), y i n = O( t + h2 ) . Можно оценить решение zi n уравнения (8) через правую часть yi n и доказать тем самым сходимость разностной схемы (6) с первым порядком по t и вторым – по h. Однако это исследование мы отложим, а сейчас на примере схемы (6) продемонстрируем один распространенный прием исследования разностных схем с постоянными коэффициентами, называемый методом гармоник . Хотя данный метод не является достаточно обоснованным, в частности не учитывает влияния граничных условий и правых частей, он позволяет легко найти необходимые условия устойчивости и сходимости разностных схем. Покажем, например, что явную схему (6) можно применять лишь при условии t £ 0,5h2 , означающем, что шаг по времени надо брать достаточно малым.
Рассмотрим уравнение
(9)
т.е. однородное уравнение, соответствующее (5). Будем искать частные решения (9), имеющие вид
yj n ( j ) = qn eijh j , (10)
где i – мнимая единица, j – любое действительное число и q – число, подлежащее определению. Подставляя (10) в уравнение (9) и сокращая на eijh j , получим
откуда найдем
(11)
Начальные условия соответствующие решениям вида (10) (их называют гармониками), ограничены. Если для некоторого j множитель q станет по модулю больше единицы, то решение вида (10) будет неограниченно возрастать при n®¥. В этом случае разностное уравнение (9) называется неустойчивым, поскольку нарушается непрерывная зависимость его решения от начальных условий. Если же |q| £ 1 для всех действительных j, то все решения вида (10) ограничены при любом n и разностное уравнение (9) называется устойчивым. В случае неустойчивости найти решение разностной задачи (6) по формулам (7) практически невозможно, так как погрешности (например погрешности округления), внесенные в начальный момент времени, будут неограниченно возрастать при увеличении n. Такие разностные схемы называются неустойчивыми.
Для уравнения (9) неравенство |q| £ 1 выполняется согласно (11) при всех j тогда и только тогда, когда g£ 0,5. Таким образом, использование схемы (6) возможно лишь при выполнении условия t£ 0,5h2 . Разностные схемы, устойчивые лишь при некотором ограничении на отношение шагов по пространству и по времени, называются условно устойчивыми. Следовательно, схема (6) возможно устойчива, причем условие устойчивости имеет вид t/h2 £ 0,5. Условно устойчивые схемы для уравнений параболического типа используются редко, так как они накладывают слишком сильное ограничение на шаг по времени. Действительно, пусть, например, h = 10-2 . Тогда шаг t не должен превосходить 0,5 * 10-4 , и для того чтобы вычислить решение yj n при t = 1 , надо взять число шагов по времени n = t-1 ³ 2 * 104 , т.е. провести не менее 2 * 104 вычислений по формулам (7).
3.3. Неявные схемы. Чисто неявной разностной схемой для уравнения теплопроводности теплопроводности (схемой с опережением) называется разностная схема, использующая шаблон (xi , tn ), (xi ± 1 , tn+1 ), (xi , tn+1 ) и имеющая вид
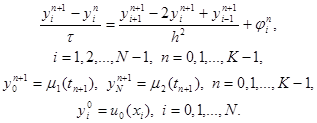 |
(12)
Здесь j n i = f(xi , tn+1 ) + O( t + h2 ) . Схема имеет первый порядок аппроксимации по t и второй – по h. Решение системы (12) находится, как и в случае явной схемы, по слоям, начиная с n = 1. Однако, теперь, в отличие от явной схемы, для нахождения yi n+1 по известным yi n требуется решить систему уравнений
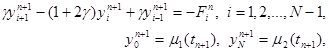 |
(13)
где g = t /h2 , Fi n = yi n + t j i n . Эту систему можно решать методом прогонки, так как условия устойчивости прогонки выполнены.
Для исследования устойчивости разностной схемы (12) будем искать частные решения уравнения
имеющие вид (10). Тогда получим
следовательно, |q| £ 1 при любых j , t , h . Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h . Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10-2 . Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.
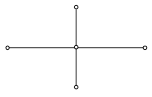
![]() Шеститочечной симметричной схемой
называется разностная схема
Шеститочечной симметричной схемой
называется разностная схема
(14)
для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.
Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему
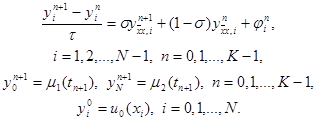 |
(15)
При s = 0 получим отсюда явную схему, при s = 1 – чисто неявную схему и при s = 0,5 – симметричную схему (14). Исследуем погрешность аппроксимации схемы (15) на решении исходной задачи (1) – (3). Представим решение задачи (15) в виде yi n = u(xi , tn ) + zi n , где u(xi , tn ) – точное решение дифференциальной задачи (1) – (3). Тогда для погрешности получим систему уравнений
(16)
i = 1, 2,…, N – 1, n = 0, 1,…, K – 1,
z0 n+1 = zN n+1 = 0, n = 0, 1,…, K – 1, zi 0 = 0, i = 0, 1,…, N.
Сеточная функция yi n , входящая в правую часть уравнения (16) и равная
![]() (17)
(17)
![]() называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции yi
n
по степеням h и t. Будем разлагать все функции, входящие в выражение для yi
n
, по формуле Тейлора в точке (xi
, tn
+ 0,5t). Учитывая разложения
называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции yi
n
по степеням h и t. Будем разлагать все функции, входящие в выражение для yi
n
, по формуле Тейлора в точке (xi
, tn
+ 0,5t). Учитывая разложения
где
получим
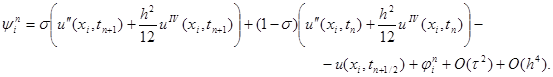 |
Отсюда, проводя разложение в точке (xi , tn+1/2 ) и обозначая u = u (xi , tn+1/2 ) , будем иметь
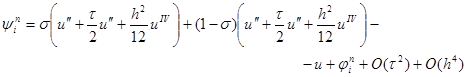 |
и, перегруппировывая слагаемые, получим, что
Учитывая уравнение (1) u’’ – u = – f и следствие из него uIV – u’’ = –f’’ , окончательно можно записать, что
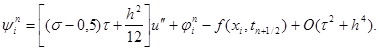 |
(18)
![]() Из формулы (18) можно сделать следующие выводы. Если
Из формулы (18) можно сделать следующие выводы. Если
то схема (15) имеет второй порядок аппроксимации по t и четвертый – по h . Такая схема называется схемой повышенного порядка аппроксимации. Если
то схема (15) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и при j i n º 0 в виде (10), то получим
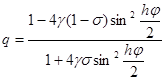 |
и |q| £ 1 при всех j, если
(19)
Отсюда видно, в частности, что все схемы с s³ 0,5 абсолютно устойчивы. Схема повышенного порядка аппроксимации (s = s* ) также абсолютно устойчива, что проверяется непосредственно.
При s¹ 0 разностная схема (15) является неявной схемой. Для нахождения решения yi n+1 по заданным yi n требуется решать систему уравнений
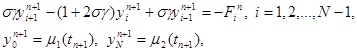 |
(20)
![]() где
где
Система (20) решается методом прогонки. Условия устойчивости прогонки при s¹ 0 сводятся к неравенству
|1 + 2 s g | ³ 2 | s | g
и выполнены при s³ – 1/(4g). Последнее неравенство следует из условия устойчивости (19) разностной схемы.
3.4. Уравнения с переменными коэффициентами и линейные уравнения. Рассмотрим первую краевую задачу для уравнения теплопроводности с переменными коэффициентами
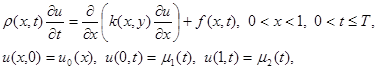 |
(21)
где r (x, t), k(x, t), f(x, t) – достаточно гладкие функции, удовлетворяющие условиям
0 < c1 £ k(x, t) £ c2 , r (x, t) ³ c3 > 0 . (22)
Дифференциальное выражение при каждом
фиксированном t аппроксимируем в точке (xi , t) так же, как и в стационарном случае, разностным отношением
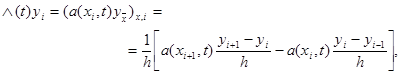 |
(23)
где разностный коэффициент теплопроводности a(xi , t) должен удовлетворять условиям второго порядка аппроксимации
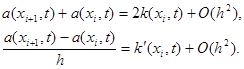 |
Наиболее употребительны следующие выражения для a(xi , t) :
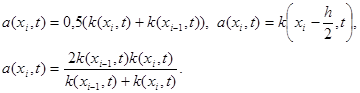 |
Разностная схема с весами для задачи (21) имеет вид
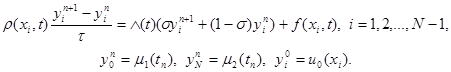 |
(24)
Здесь в качестве t можно взять любое значение t Î [tn , tn+1 ] , например t = tn + 0,5 t . Если в уравнении (24) t = tn + 0,5 t , s = 0,5 , то схема (24) имеет второй порядок аппроксимации по t и по h . При остальных значениях s и t выполняется первый порядок аппроксимации по t и второй – по h .
При исследовании устойчивости разностных схем с переменными коэффициентами иногда применяется принцип замороженных коэффициентов, сводящий задачу к уравнению с постоянными коэффициентами. Рассмотрим явную схему, соответствующую уравнению (24) с s = 0 и f(xi , t) º 0 , т.е. схему
(25)
Предположим, что коэффициенты r (xi , t), a(xi , t) – постоянные, r (xi , t) º r = const, a(xi , t) º a = const . Тогда уравнение (25) можно записать в виде
![]() или
или
Из п.2 известно, что последнее уравнение устойчиво при t ’ £ 0,5h2 , т.е. при
(26)
Принцип замороженных коэффициентов утверждает, что схема (25) устойчива, если условие (26) выполнено при всех допустимых значениях a(xi , t), r (xi , t) , т.е. если при всех x, t выполнены неравенства
(27)
Если известно, что 0 < c1 £ a(xi , t) £ c2 , r (xi , t) ³ c3 > 0 , то неравенство (27) будет выполнено при
Строгое обоснование устойчивости схемы (25) будет дано в примере 2 из главы 2.
Если параметр s³ 0,5, то из принципа замороженных коэффициентов следует абсолютная устойчивость схемы (24).
Рассмотрим теперь первую краевую задачу для нелинейного уравнения теплопроводности
(28)
В случае нелинейных уравнений, когда заранее неизвестны пределы изменения функции k(u) , избегают пользоваться явными схемами. Чисто неявная схема, линейная относительно yi n+2 , i = 1, 2,…, N – 1 , имеет вид
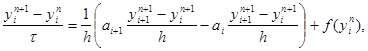 |
(29)
где ai = 0,5 (k(yn i ) + k(yn i-1 )) . Эта схема абсолютно устойчива, имеет первый порядок аппроксимации по t и второй – по h . Решение yi n+1 , i = 1, 2,…, N – 1 , находится методом прогонки. Заметим, что схему (29) можно записать в виде
где ki = k(yi n ) .
Часто используется нелинейная схема
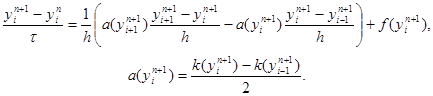 |
(30)
Для реализации этой схемы необходимо применить тот или иной итерационный метод. Например такой:
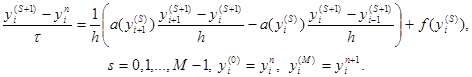
(31)
Здесь s – номер итерации. Как видим, нелинейные коэффициенты берутся с предыдущей итерации, а в качестве начального приближения для yi n+1 выбирается yi n . Это начальное приближение тем лучше, чем меньше шаг t. Число итераций M задается из соображений точности. В задачах с гладкими коэффициентами при k(u) ³ c1 > 0 часто бывает достаточно провести две – три итерации. Значения yi (S+1) на новой итерации находятся из системы (31) методом прогонки. При M = 1 итерационный метод (31) совпадает с разностной схемой (29).
Для приближенного решения нелинейного уравнения (28) применяются также схемы предиктор – корректор второго порядка точности, аналогичные методу Рунге – Кутта для обыкновенных дифференциальных уравнений. Здесь переход со слоя n на слой n+1 осуществляется в два этапа. Приведем пример такой схемы. На первом этапе решается неявная линейная система уравнений
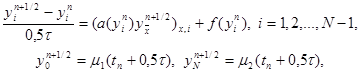 |
из которой находятся промежуточные значения yi n+1/2 , i = 0, 1,…, N . Затем на втором этапе используется симметричная шеститочечная схема для уравнения (28), в которой нелинейные коэффициенты a(y), f(y) вычисляются при y = yi n+1/2 , т.е. схема
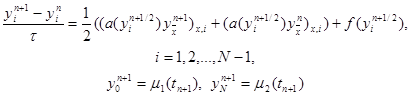 |
Похожие работы
-
Решение смешанной задачи для уравнения гиперболического типа методом сеток
Решение смешанной задачи для уравнения гиперболического типа методом сеток Рассмотрим смешанную задачу для волнового уравнения ) (1). Задача состоит в отыскании функции
-
Двухсеточный метод решения уравнения Лапласа
Министерство образования и науки РФ Государственное образовательное учреждение высшего профессионального образования «Якутский государственный университет им. М.К.Аммосова»
-
Метод конечных разностей или метод сеток
ВВЕДЕНИЕ Значительнаое число задач физики и техники приводят к дифференциальным уравнениям в частных прозводных (уравнения математической физики). Установившиеся процессы различной физической природы описываются уравнениями эллиптического типа.
-
Решение задач по эконометрике 2
Задача 1 Вариант Провести корреляционно регрессионный анализ в зависимости выплаты труда от производительности труда для этого: 1. Построить поле корреляции и выбрать модель уравнения.
-
Решения смешанной задачи для уравнения гиперболического типа методом сеток
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Р.Ф. КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра прикладной и высшей математики Лабораторная работа № 43
-
Конечно-разностный метод решения для уравнений параболического типа
Общая характеристика параболических дифференциальных уравнений на примере уравнения теплопроводности. Основные определения и конечно-разностные схемы. Решение дифференциальных уравнений параболического типа методом сеток или методом конечных разностей.
-
Приближенное решение интегрального уравнения
Решение краевой задачи. Методы конечно-разностных, центрально-разностных отношений и метод прогонки. Приближенное решение линейного дифференциального уравнения второго порядка с помощью методов Галеркина, Ритца и коллокации, сравнение результов.
-
Решение параболических уравнений
Описание общих принципов метода сеток, его применение к решению параболических уравнений. Исследование разрешимости получаемой системы разностных уравнений. Разработка программы для численного решения поставленной задачи, выполнение тестовых расчетов.
-
Разностные схемы для уравнений параболического типа
Уравнения параболического типа. Разностные схемы для уравнения теплопроводности, задача Коши. Явная и неявная разностные схемы. Применение двухслойных разностных шаблонов. Устойчивость двухслойных разностных схем. Решение задач методом прогонки.
-
Краевые задачи и разностные схемы
Приведение к системе уравнений первого порядка. Разностное представление систем дифференциальных уравнений. Сеточные методы для нестационарных задач. Особенность краевых задач второго порядка. Разностные схемы для уравнений в частных производных.