Название: Граничні теореми теорії ймовірностей
Вид работы: реферат
Рубрика: Математика
Размер файла: 47.67 Kb
Скачать файл: referat.me-217574.docx
Краткое описание работы: Оцінка ймовірності відхилення випадкової величини Х від її математичного сподівання. Знаходження дисперсії випадкової величини за допомогою теореми Бернуллі. Застосування для випадкової величини нерівності Чебишова. Суть центральної граничної теореми.
Граничні теореми теорії ймовірностей
Міністерство освіти і науки України
Приватний вищий навчальний заклад
Європейський університет
Запорізька філія
Реферат
Граничні теореми теорії ймовірностей
з дисципліни: Теорія ймовірностей та математична статистика
Запоріжжя,
2007р.
Теорема Бернуллі. Нехай імовірність появи події А в кожному із п незалежних повторних випробувань дорівнює р, т - число появ події А (частота події) в п випробуваннях. Тоді
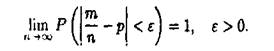
Доведення. Частість ![]() можна розглядати як невід'ємну випадкову величину
можна розглядати як невід'ємну випадкову величину![]() . Знайдемо її математичне сподівання
. Знайдемо її математичне сподівання
![]()
Отже, необхідно оцінити імовірність відхилення випадкової величини![]() від її математичного сподівання. Для цього знайдемо дисперсію цієї випадкової величини
від її математичного сподівання. Для цього знайдемо дисперсію цієї випадкової величини
![]()
За нерівністю Чебишова одержимо
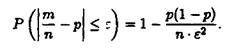
Звідси граничним переходом![]() одержуємо (4), що й треба було довести.
одержуємо (4), що й треба було довести.
Теорема Чебишова. Нехай ![]() - послідовність попарно незалежних випадкових величин, які задовольняють умовам
- послідовність попарно незалежних випадкових величин, які задовольняють умовам
![]()
для усіх t= 1,2,..., п.
Тоді![]()
Доведення. Знайдемо математичне сподівання та дисперсію![]() середньої випадкових величин, тобто
середньої випадкових величин, тобто
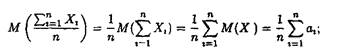
![]()
Застосуємо для випадкової величини нерівність Чебишова (2)
![]()
![]()
Границя цієї імовірності при ![]() дорівнює одиниці, тобто рівність (5) доведено.
дорівнює одиниці, тобто рівність (5) доведено.
Центральна гранична теорема. Нехай задана послідовність незалежних однаково розподілених випадкових величин
![]()
![]()
Розглянемо випадкову величину![]() Тоді
Тоді
![]()
При![]() функція розподілу
функція розподілу
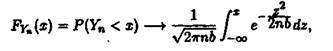
тобто сума![]() буде розподілена за нормальним законом з математичним сподіванням 0 та дисперсією
буде розподілена за нормальним законом з математичним сподіванням 0 та дисперсією![]()
Для доведення цієї теореми треба знайти границю характеристичної функції, побудованої для нормованої випадкової величини
![]()
Наслідок. При ![]() розподіл суми однаково розподілених випадкових величин мало відрізняється від нормального розподілу.
розподіл суми однаково розподілених випадкових величин мало відрізняється від нормального розподілу.
Теорема Ляпунова. Нехай задана послідовність незалежних випадкових величин ![]() таких, що
таких, що
![]()
Побудуємо суму випадкових величин ![]() Позначимо
Позначимо![]() Якщо виконується умова рівномірної малості величин, що утворюють суму
Якщо виконується умова рівномірної малості величин, що утворюють суму
![]()
![]() то сума
то сума![]() буде розподіленою нормально з математичним сподіванням
буде розподіленою нормально з математичним сподіванням![]() та дисперсією
та дисперсією
Доведення цієї теореми досить складне, але відмітимо, що у випадку, коли![]() можна розглядати випадкові величини
можна розглядати випадкові величини![]() Величини
Величини![]() будуть задовольняти умову теореми Ляпунова.
будуть задовольняти умову теореми Ляпунова.
Приклад 2. Скільки додатків треба взяти у теоремі Чебишова, щоб з надійністю 96% і точністю до 0.01 виконувалась наближена рівність
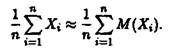
Розв'язок. В цьому прикладі є = 0.01. Щоб одержати надійність 96% згідно формули (6) достатньо підібрати таке п, яке задовольняє нерівність
![]()
Зауваження 1. Приклад 2 показує, що навіть у випадку не дуже великих точності та надійності, треба брати значну кількість додатків (п - досить велике число). Це означає, що оцінки, одержані з використанням нерівності (6), - завищені. Більш точні оцінки можна одержати за допомогою теореми Ляпунова.
Список використаної літератури
1. Барковський В.В., Барковська Н.В., Лопатін О.К. теорія ймовірностей та математична статистика. – К.: ЦУЛ, 2002. – 448с.
2. Гмурман В.Е. теория вероятностей и математическая статистика. – М.: Высшая школа, 1980.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1975.
4. Гнеденко Б.В. Курс теории вероятностей. – М.: наука, 1988.
5. Леоненко М.М., Мішура Ю.С. та ін. Теоретико-ймовірностні та статистичні методи в економетриці та фінансовій математиці. – К.: Інформтехніка, 1995.
Похожие работы
-
Основні теореми теорії ймовірностей
Тема 2. Основні теореми теорії імовірності На фундаменті міцному будем класти поверхи, перегородки та сходинки, що їх з’єднають на віки. План. Теорема додавання імовірностей несумісних подій..
-
Теорія ймовірності та її застосування в економіці
Контрольна робота З дисципліни: Теорія ймовірностей та математична статистика Прізвище,ім’я, по-батькові студента Данiщук Мирослава Евгенiївна
-
Випадкова величина
ТЕМА ВИПАДКОВА ВЕЛИЧИНА 1 Випадкова величина. Функція розподілу випадкової величини Зіставимо кожну елементарну подію конкретного випробування з деяким числом. Наприклад, розглянемо випробування, що полягає в підкиданні монети. Маємо простір елементарних подій – множину з двох можливих рівно ймовірних наслідків випробування: w
-
Густина розподілу імовірностей одновимірної і багатовимірної випадкових величин
Реферат на тему: Густина (щільність) розподілу імовірностей одновимірної і багатовимірної випадкових величин” a.Густина розподілу (щільність імовірності).
-
Системи випадкових величин
Розподіли системи двох випадкових величин, що однозначно визначається сумісним розподілом ймовірностей, який можна задати матрицею. Інтегральна функція розподілу випадкового вектора. Середньоквадратична регресія. Лінійна кореляція нормальних величин.
-
Загальні положення теорії ймовірностей та математичної статистики
Реферат на тему: Загальні положення теорії ймовірностей та математичної статистики План Основні поняття та визначення: поняття стохастичної с-ми експерименту, ймовірності, випадкової величини.
-
Оцінювання параметрів розподілів
ОЦІНЮВАННЯ ПАРАМЕТРІВ РОЗПОДІЛІВ Задача оцінювання параметрів розподілів полягає в побудові на основі статистичної інформації, отриманої за даними вибірки, статистичних висновків про істинне значення невідомого параметра
-
Числові характеристики системи випадкових величин та їх граничні теореми
Властивості числових характеристик системи випадкових величин. Обчислення кореляційного моменту. Ведення комплексної випадкової величини, характеристичні функції. Види збіжності випадкових величин. Приклади доказів граничних теорем теорії ймовірностей.
-
Розрахунок типових задач з математичної статистики
Закон розподілення дискретної випадкової величини, подання в аналітичній формі за допомогою функції розподілення ймовірності. Числові характеристики дискретних випадкових величин. Значення критерію збіжності Пірсона. Аналіз оцінок математичного чекання.
-
Теорія ймовірностей та математична статистика
Знаходження ймовірності настання події у кожному з незалежних випробувань. Знаходження функції розподілу випадкової величини. Побудова полігону, гістограми та кумуляти для вибірки, поданої у вигляді таблиці частот. Числові характеристики ряду розподілу.