Название: Методы решения биматричных игр

Вид работы: реферат

Рубрика: Математика

Размер файла: 61.3 Kb

Скачать файл: referat.me-217814.docx

Краткое описание работы: Основные определения теории биматричных игр. Пример биматричной игры "Студент-Преподаватель". Смешанные стратегии в биматричных играх. Поиск "равновесной ситуации". 2x2 биматричные игры и формулы для случая, когда у каждого игрока имеется две стратегии.

Методы решения биматричных игр

МЕТОДЫ РЕШЕНИЯ БИМАТРИЧНЫХ ИГР

1. Основные определения теории биматричных игр

Рассмотрим конфликтную ситуацию, в которой каждый из двух участников имеет следующие возможности для выбора своей линии поведения:

игрок А – может выбрать любую из стратегий А₁ , ... , А_т ,

игрок В – любую из стратегий В₁ , …, В _n

При этом всякий раз их совместный выбор оценивается вполне определенно:

если игрок А выбрал i -ю стратегию , а игрок В – k -ю стратегию , то в итоге выигрыш игрока А будет равен некоторому числу , а выигрыш игрока В некоторому, вообще говоря, другому числу .

Иными словами, всякий раз каждый из игроков получает свой приз.

Последовательно перебирая все стратегии игрока А и все стратегии игрока В, мы сможем заполнить их выигрышами две таблицы (первая из них описывает выигрыши игрока А, а вторая – выигрыши игрока В).

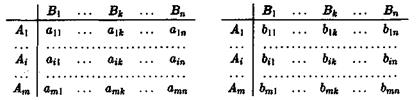
Обычно эти таблицы записывают в виде матриц

Здесь А – платежная матрица игрокаА , а В – платежная матрица игрокаВ .

При выборе игроком А i -й стратегии, а игроком В – k -й стратегии их выигрыши находятся в матрицах выплат на пересечении i -х строк и k -x столбцов: в матрице А это элемент , а в матрице В – элемент .

Таким образом, в случае, когда интересы игроков различны (но не обязательно противоположны), получаются две платежные матрицы: одна – матрица выплат игроку А , другая – матрица выплат игроку В . Поэтому совершенно естественно звучит название, которое обычно присваивается подобной игре – биматричная .

Замечание. Рассматриваемые матричные игры, можно рассматривать и как биматричные, где матрица выплат игроку В противоположна матрице выплат А :

В общем случае биматричная игра – это игра с ненулевой суммой .

Класс биматр. игр значительно шире класса матричных (разнообразие новых моделируемых конфликтных ситуаций весьма заметно), а, значит, неизбежно увеличиваются и трудности, встающие на пути их успешного разрешения.

Пример. «Студент — Преподаватель».

Рассмотрим следующую ситуацию. Студент (игрок А ) готовится к зачету, который принимает Преподаватель (игрок В ). Можно считать, что у Студента две стратегии – подготовиться к сдаче зачета (+) и не подготовиться (-). У Преподавателя также две стратегии – поставить зачет [+] и не поставить зачета [-].

В основу значений функций выигрыша игроков положим следующие соображения:

Количественно это можно выразить, например, так

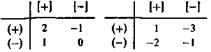
2. Смешанные стратегии в биматричных играх

В приведенных примерах описаны ситуации, в которых интересы игроков не совпадают. Встает вопрос о том, какие рекомендации необходимо дать игрокам для того, чтобы моделируемая конфликтная ситуация разрешилась. Иными словами, что мы будем понимать под решением биматричной игры?

Попробуем ответить на это вопрос так:

вследствие того, что интересы игроков не совпадают, нам нужно построить такое (компромиссное) решение, которое бы в том или ином, но в одинаковом смысле удовлетворяло обоих игроков.

Не пытаясь сразу выражать эту мысль совсем точно, скажем – попробуем найти некую равновесную ситуацию , явное отклонение от которой одного из игроков уменьшало бы его выигрыш.

Подобный вопрос мы ставили и при рассмотрении матричных игр. Напомним, что возникающее при разработке минимаксного подхода понятие равновесной ситуации приводило нас к поиску седловой точки, которая, существует не всегда – конечно, если ограничиваться только чистыми стратегиями игроков А и В , т.е. стратегиями .

Однако при расширении матричной игры путем перехода к смешанным стратегиям, т. е. к такому поведению игроков, при котором они чередуют (чистые) стратегии с определенными частотами:

игрок А – стратегии A ₁ ,..., А_т с частотами р₁ ,..., р_т , где

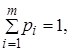
а игрок В – стратегии В₁ ,...., В _n , с частотами q ₁ ,..., q_n , где

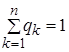
выяснилось, что в смешанных стратегиях равновесная ситуация всегда существует. Иными словами, любая матричная игра в смешанных стратегиях разрешима .

Поэтому, рассматривая здесь биматричные игры, разумно попробовать сразу же перейти к смешанным стратегиям игроков (этим мы предполагаем, что каждая игра может быть многократно повторена в неизменных обстоятельствах).

В матричном случае смешивание стратегий приводило к расширению возможности выплат в том смысле, что расчет строился из вычисления средних выигрышей игроковА иВ , которые определялись по элементам платежной матрицы А и вероятностям и :

,

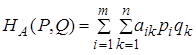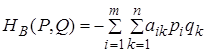
При смешанных стратегиях в биматричных играх также возникают средние выигрыши игроков А иВ , определяемые по правилам, в которых уже нет никакой дискриминации игрока В :

,

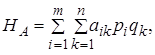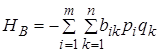
3. 2x2 биматричные игры. Ситуация равновесия

Мы предполагаем уделить основное внимание случаю, когда у каждого из игроков имеется ровно две стратегии, т. е. случаю т = п = 2. Поэтому нам кажется уместным выписать приведенные выше формулы именно для такого случая.

В 2 ´ 2 биматричной игре платежные матрицы игроков имеют следующий вид

, ,

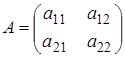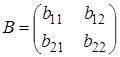вероятности

биматричная игра решение

а средние выигрыши вычисляются по формулам

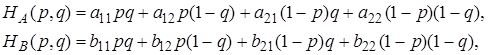
где

,

Сформулируем основное определение.

Определение. Будем считать, что пара чисел

, ,

определяет равновесную ситуацию , если для любых р и q , подчиненных условиям одновременно выполнены следующие неравенства

(1)

Пояснение . Выписанные неравенства (1) означают следующее: ситуация, определяемая смешанной стратегией (р*, q *), является равновесной , если отклонение от нее одного из игроков при условии, что другой сохраняет свой выбор, приводит к тому, что выигрыш отклонившегося игрока может только уменьшиться. Тем самым, получается, что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку.

Теорема 1 (Дж. Нэш). Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.

Итак, равновесная ситуация существует. Но как ее найти?

Если некоторая пара чисел (р*, q *) претендует на то, чтобы определять ситуацию равновесия, то для того, чтобы убедиться в обоснованности этих претензий, или, наоборот, доказать их необоснованность, необходимо проверить справедливость неравенств (1) для любого р в пределах от 0 до 1 и для любого q впределах от 0 до 1. В общем случае число таких проверок бесконечно. И, следовательно, действенный способ определения равновесной ситуации нужно искать где-то в ином месте.

Теорема 2. Выполнение неравенств

(1)

равносильно выполнению неравенств

(2)

Иными словами, для того, чтобы убедиться в обоснованности претензий пары (р*, q *) на то, чтобы определять равновесную ситуацию, нужно проверить справедливость неравенства

только для двух чистых стратегий игрока А (р = 0 и р = 1 ) и неравенства

только для двух чистых стратегий игрока В ( q = 0 иq = 1).

Четыре неравенства (2) позволяют провести поиск точки равновесия вполне конструктивно.

Запишем средние выигрыши игроков А и В в более удобной форме.

Имеем

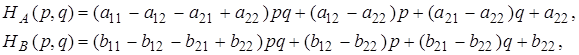
Обратимся к первой из полученных формул.

Полагая в ней сначала р = 1, а потом р = 0, получаем,

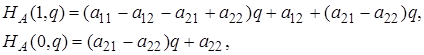
Рассмотрим разности

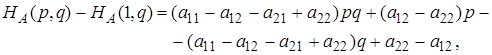
Полагая

получим для них следующие выражения

В случае, если пара (р , q ) определяет точку равновесия, эти разности неотрицательны

Поэтому окончательно получаем

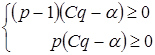
Из формул для функции н_в ( р, q ) при q = 1 и q = 0 соответственно имеем

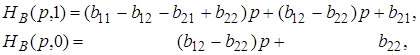
Разности

и

с учетом обозначений

.

приводятся к виду

совершенно так же, как соответствующие разности для функции Н_А .

Если пара (р , q ) определяет точку равновесия, то эти разности неотрицательны

Поэтому

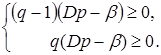
Вывод

Для того, чтобы в биматричной игре

, ,

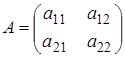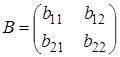пара (р, q ) определяла равновесную ситуацию , необходимо и достаточно одновременное выполнение следующих неравенств

, ,

, ,

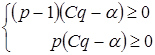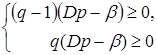где

.