Название: Экспоненциальный фильтр

Вид работы: лабораторная работа

Рубрика: Математика

Размер файла: 87.06 Kb

Скачать файл: referat.me-217852.docx

Краткое описание работы: Лабораторная работа № 2 ЭКСПОНЕНЦИАЛЬНЫЙ ФИЛЬТР Цель работы Ознакомиться с аналоговым и дискретным вариантами реализации фильтра Общие сведения аналоговом

Экспоненциальный фильтр

Лабораторная работа № 2

ЭКСПОНЕНЦИАЛЬНЫЙ ФИЛЬТР

Цель работы

Ознакомиться с аналоговым и дискретным вариантами реализации фильтра

Общие сведения

В аналоговом варианте экспоненциальный фильтр представляет собой апериодическое звено и описывается дифференциальным уравнением

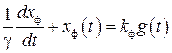, (15)

где и – параметры настройки фильтра.

Уравнению (15) соответствует амплитудно-фазовая характеристика (АФХ)

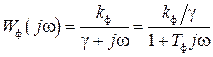, (16)

где 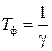– постоянная времени фильтра.

Из условия (3) (математическое ожидание) для статического режима определяют оптимальное значение параметра . Коэффициент усиления

. (17)

Определение оптимального значения параметра производится из условия (4) (среднеквадратичная погрешность оценки).

Для этого предварительно рассчитывают спектральную плотность погрешности экспоненциального фильтра по формуле (7) с учётом (16) и (17).

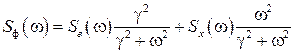. (18)

Дисперсия погрешности экспоненциального фильтра, согласно (6), (7), с учётом (16), равна

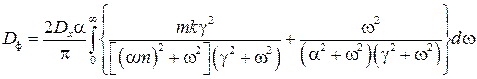. (19)

При вычислении этого интеграла оба слагаемых подынтегрального выражения раскладывают на простые дроби, каждая из которых сводится к табличному интегралу вида

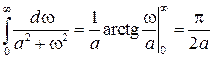. (20)

После выполнения соответствующих преобразований получают следующее выражение для дисперсии погрешности фильтрации:

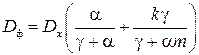. (21)

Оптимальное значение параметра настройки получают из необходимого условия экстремума функции :

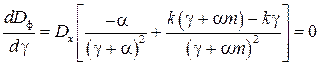. (22)

Откуда оптимальное значение параметра

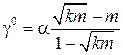. (23)

Таким образом, функция имеет единственную точку стационарности, тип которой зависит от знака второй производной при .

Можно показать, что при выполнении условия

, (24)

особая точка является минимумом функции , а при выполнении условия

(25)

в точке , функция достигает максимума.

Таким образом, если сочетание характеристик полезного сигнала и помехи соответствуют случаю (24), то оптимальное значение параметра настройки определяется по формуле (23).

Если это условие не выполняется, то оптимальным является наибольшее допустимое значение параметра .

При программной реализации экспоненциального фильтра дифференциальное уравнение (15) заменяют разностным уравнением вида

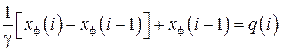(26)

где i – номер цикла расчёта

Отсюда получают следующее рекуррентное соотношение для вычисления сглаженного значения в очередном i -том цикле расчёта:

(27)

К достоинствам алгоритма экспоненциальной фильтрации относятся: малая трудоёмкость расчётов и малый объём памяти ЭВМ, в которой должны храниться величина и обновляемая в каждом цикле расчёта величина .

Пример выполнения лабораторной работы с использованием пакета MCAD представлен в Приложении 3 к лабораторной работе №2. Здесь представлен вариант расчёта трёхкратного сглаживания экспериментальных данных, полученных от ИИК технологического процесса, построены графики.

Общая часть заданий

1. Ознакомиться с теоретическим описанием

2. Выполнить расчёты в MCAD сглаженных значений данных полученных от ИИК. Для расчётов пользоваться формулами:

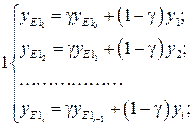
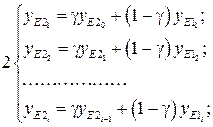
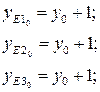
За начало отсчёта примем следующие допущения:

Расчёт произвести для трёх значений g:

g = 0,4; 0,5; 0,6

3. Провести анализ полученных зависимостей на выполнение фильтрации полезного сигнала от помехи

4. Сделать выводы и дать предложения о возможности применения сглаживающего фильтра для уменьшения помех