Referat.me
/ / Раціональні дроби та їх властивості

Название: Раціональні дроби та їх властивості

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 51.53 Kb

Скачать файл: referat.me-217880.docx

Краткое описание работы: м. Комсомольськ гімназія ім. В.О.Ніжніченка ПРАКТИЧНА РОБОТА на тему „Раціональні дроби та їх властивості” підготувала Шепель Ілона 2004 р. Дріб, числівник і знаменник якого є многочленами, називається

Раціональні дроби та їх властивості

м. Комсомольськ

гімназія ім. В.О.Ніжніченка

ПРАКТИЧНА РОБОТА

на тему

„Раціональні дроби та їх властивості”

підготувала

Шепель Ілона

2004 р.

Дріб, числівник і знаменник якого є многочленами, називається раціональним (алгебраїчним).

Наприклад,

; ; ;

є раціональними або алгебраїчними дробами.

Область припустимих значень (ОПЗ) алгебраїчного дробу є множина всіх числових наборів, що відповідають набору многочленів P та Q, для кожного з яких значення многочлена Q не дорівнює нулю.

Наприклад,

(ОПЗ) алебраїчного дробу є множина всіх числових наборів, відповідаючих її буковному наборові (a,b,c) таких що

Два раціональні дроби та тотожньо рівні на множині М, якщо на множині М справедлива рівність PB=QA, за умови, що многочлени Q та B не дорівнюють нулю.

Наприклад,

Справедлива тотожня рівність

для так як для них виконується


Основна властивість дробу виражена тотожністю , яка справедлива за умов , де R – цілий раціональний вираз (многочлен, одночлен або число).

Приведення раціональних дробів до спільного знаменника .

Скоротити дріб – це означає розділити числівник і знаменник дробу на спільний множник. Можливість такого скорочення обумовлена основною властивістю дробу.

Спільним знаменником декілька раціональних дробів називається цілий раціональний вираз, який ділиться на знаменник кожного дробу.

Для того, щоб декілька раціональних дробів привести до спільного знаменника, потрібно:

  1. Розкласти знаменник кожного дробу на множники;
  2. Скласти загальний знаменник, включивши в нього в якості співмножників всі множники одержаних розкладів; якщо множник є в декількох розкладах, то він береться з найбільшим показником ступеню;
  3. Знайти додаткові множники для кожного з дробів (для цього спільний знаменник ділять на знаменник дробу);
  4. Домноживши числівник і знаменник на додатковий множник, привести дроби до спільного знаменника.

Додавання і віднімання раціональних дробів.

Сума двох (любої скінченної кількості) раціональних дробів з однаковими знаменниками дорівнює дробу з тим же знаменником і з числівником, що дорівнює сумі числівників дробів-доданків:

.

Аналогічно і в випадку віднімання дробів з однаковими знаменниками:

.

Для додавання і віднімання раціональних дробів з різними знаменниками потрібно привести дроби до спільного знаменника, а потім виконати операції над дробами з однаковими знаменниками.

Наприклад :

Спростити вираз: .

Розв”язок .


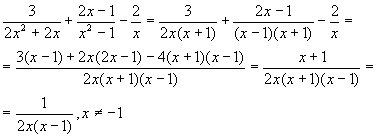Множення і ділення раціональних дробів .

Добуток двох (любої скінченної кількості) раціональних дробів тотожньо дорівнює дробу, числівник якого дорівнює добутку числівників, а знаменник – добутку знаменників дробів-співмножників:

.

Час тка від ділення двох раціональних дробів тотожньо дорівнює дробу, числівник якого дорівнює добутку числівника першого дробу на знаменник другого дробу, а знаменник - добутку знаменника першого дробу на числівник другого дробу:

.

Наприклад :

Виконати множення.

Розв”язок.

.

Піднесення раціонального дробу до степеня.

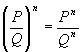Для того, щоб піднести раціональний дріб до натурального степеню n , треба піднести до цього степеня окремо числівник і знаменник дробу. Перший вираз – числівник, другий вираз – знаменник результата. .

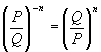При піднесенні дробу до цілого від”ємного степеня використовуємо тотожність

яка справедлива при будь-яких значеннях змінних , за яких P ¹ 0, Q ¹ 0.

Перетворення раціональних виразів

Перетворення будь-якого раціонального виразу можна звести до додавання, віднімання, множення та ділення раціональних дробів, а також до піднесення дробу до натурального степеня. Будь-який раціональний вираз можна перетворити на дріб, числівник і знаменник якого – цілі раціональні вирази; в цьому, як правило, є ціль тотожніх перетворень раціональних виразів.

Наприклад :

Спростити вираз

.

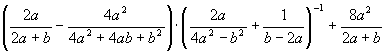Розв”язок.

О. П. З.: .

;

;

  1. ;

;

  1. .

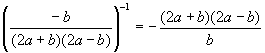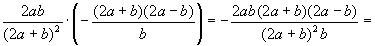
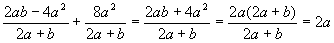Література:

1. М.Я. Выгодский, „Справочник по элементарной математике”, Москва, 1949

2. В.В. Вавилов, И.И. Мельников, „Задачи по математике. Алгебра”, Москва, 1987

Похожие работы