Referat.me
/ / Типовой расчет по ЭМММ

Название: Типовой расчет по ЭМММ

Вид работы: реферат

Рубрика: Математика

Размер файла: 21.52 Kb

Скачать файл: referat.me-218020.docx

Краткое описание работы: Типовой расчет Решение задач по дисциплине ЭМММ Вариант №23 Выполнил: Проверил: Екатеринбург 2009 Математическая модель ЗЛП Мат. модель ЗЛП называется стандартной, если система ограничений представлена в виде неравенств, а функция минимизируется или максимизируется

Типовой расчет по ЭМММ

Типовой расчет

Решение задач

по дисциплине ЭМММ

Вариант №23

Выполнил:

Проверил:

Екатеринбург

2009
Математическая модель ЗЛП

Мат. модель ЗЛП называется стандартной, если система ограничений представлена в виде неравенств, а функция минимизируется или максимизируется

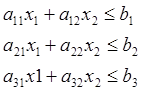
- система ограничений


- целевая функция

X=(x1,x2) – основное (оптимальное) решение

(>= в системе ограничений min )

Целевая f(x) является линейной, поэтому частные производные отличны от нуля, т к является const, следовательно экстремальных значений внутри области ограничений нет. Если функция имеет оптимальное значение, то оно достигается на границах области.


Задача:

Предприятие выпускает 2 вида продукции А1 и А2, использую при этом 3 вида сырья S1, S2, S3. Известны запасы сырья- b1, b2, b3. Расход сырья вида Si на производство продукции Aj=aij.Доход от реализации одной единицы продукции Aj составляет Сj у.е.

Требуется составить такой план производства продукции, при котором доход будет максимален.

Решить задачу графическим методом; составить каноническую модель задачи и решить её симплекс методом; Найти двойственные оценки цен на сырье из решения симметричной двойственной задачи по теоремам двойственности.

Сырье

А1

А2

bi

S1

5

2

40

S2

1

3

30

S3

4

3

39

Cj

2

3

Решение задачи графическим методом


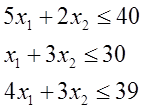f(X) = 2x + 3x max

L1: 5х + 2х = 40 | : 40

x / 8 + x / 20 = 1

L2 : x + 3x =30 | : 30

x / 30 + x / 10 = 1

L3 : 4х + 3х = 39

Х

0

9,75

Х

13

0

Взяла линейку и двигаю перпендикулярно к выходу из области.

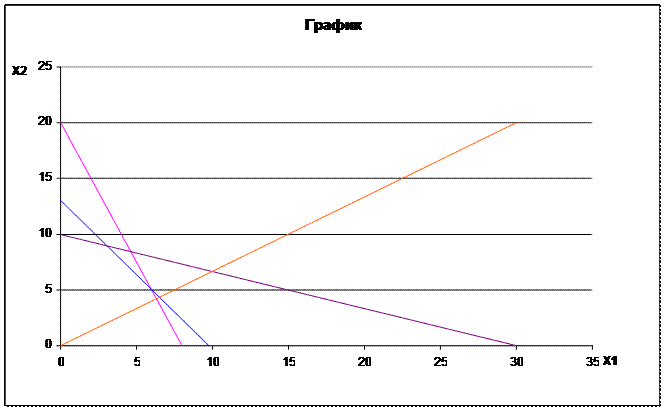
Найдем координаты точки Е = L2 L3

x + 3x = 30

4x + 3x = 39

-3x = -9

x = 3

3 + 3x = 30

x = 9

X(3;9) f(X) = 2*3+3*9=33 y.e.

Проверим:

F= L1 L3

5x + 2x = 40 | *4

4x + 3x = 39 | * 5

20x + 8x = 160

20x + 15x = 195

-7x = -35

x = 5

5x + 2*5 = 40

5x = 30

x = 6

X(6;5) f(X) = 2*6 + 3*5 = 27 y.e.

f(3;9) > f(6;5)

Ответ: Xmax = (3;9)

f(Xmax) = 33 y.e.

Похожие работы