Название: Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса
Вид работы: курсовая работа
Рубрика: Математика
Размер файла: 556.72 Kb
Скачать файл: referat.me-218165.docx
Краткое описание работы: Математический факультет Кафедра информатики и прикладной математики КУРСОВАЯ РАБОТА НА ТЕМУ: «УМЕНЬШЕНИЕ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ СТАЦИОНАРНОГО СЛУЧАЙНОГО ПРОЦЕССА»
Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса
Математический факультет
Кафедра информатики и прикладной математики
КУРСОВАЯ РАБОТА НА ТЕМУ:
«УМЕНЬШЕНИЕ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ СТАЦИОНАРНОГО СЛУЧАЙНОГО ПРОЦЕССА»
Брест 2009

![]() СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
3. ОКНА ПРОСМОТРА ДАННЫХ
ЗАКЛЮЧЕНИЕ
СПИСОКИСПОЛЬЗОВАННЫХИСТОЧНИКОВ
ПРИЛОЖЕНИЕ
 ВВЕДЕНИЕ
ВВЕДЕНИЕ
Почти в каждой области встречаются явления, которые интересно и важно изучать в их развитии и изменении во времени. В повседневной жизни могут представлять интерес, например, метеорологические условия, цены на тот или иной товар, те или иные характеристики состояния здоровья индивидуума и т.п. Все они изменяются во времени. Совокупность измерений какой-либо одной характеристики подобного рода и представляет собой временной ряд.
Одной из главных задач спектрального анализа временных рядов является построение и исследование оценок спектральных плотностей стационарных случайных процессов, так как они дают важную информацию о структуре процесса.
Методы анализа временных рядов широко используются в различных областях науки и техники, их можно применять при анализе больших объемов данных, получаемых в процессе вибрационных испытаний или извлекаемых из сводок экономических данных.
В данной работе исследована оценка спектральной плотности, построенная с использованием различных окон просмотра данных. Построены графики этой оценки для временного ряда, представляющего собой последовательность наблюдений - температуры воздуха в городе Бресте с октября 2008 по февраль 2009 года.
Графики построены также для центрированного случайного процесса.
![]() 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
Векторным временным рядом (r-мерным временным рядом) называется совокупность функций вида
![]() .
.
Переменная t обычно соответствует времени выполнения или регистрации наблюдений и измерений.
Действительным случайным процессом
![]() =
= ![]() называется семейство случайных величин, заданных на вероятностном пространстве
называется семейство случайных величин, заданных на вероятностном пространстве ![]() , где
, где ![]()
![]() ,
, ![]() ,
, ![]() - некоторое параметрическое множество.
- некоторое параметрическое множество.
Если ![]() , или
, или ![]() - подмножество из
- подмножество из ![]() , то говорят, что
, то говорят, что ![]() ,
, ![]() - случайный процесс с дискретным временем
.
- случайный процесс с дискретным временем
.
Если ![]() , или
, или ![]() подмножество из
подмножество из ![]() , то говорят, что
, то говорят, что ![]() ,
, ![]() - случайный процесс с непрерывным временем.
- случайный процесс с непрерывным временем.
Введем характеристики случайного процесса ![]() ,
, ![]() , во временной области.
, во временной области.
Математическим ожиданием
случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
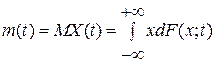 ,
,
где ![]() .
.
Дисперсией
случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
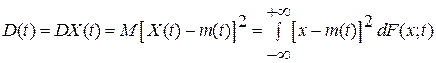 ,
,
где ![]() .
.
Спектральной плотностью
случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
![]() =
=![]()
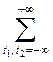
![]()
![]() ,
,
![]() ,
,
при условии, что
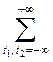
![]() .
.
Нормированной спектральной плотностью
случайного процесса ![]() называется функция вида
называется функция вида
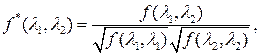
где ![]() , если
, если ![]() и
и ![]() , если
, если ![]() .
.
Из определения видно, что спектральная плотность ![]() непрерывная, периодическая функция с периодом, равным
непрерывная, периодическая функция с периодом, равным ![]() по каждому из аргументов.
по каждому из аргументов.
Ковариационной функцией
случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
![]()
![]()
![]() .
.
Смешанным моментом ![]() го порядка
,
го порядка
, ![]() , случайного процесса
, случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
![]()
![]() ,
, ![]() ,
, ![]() .
.
Заметим, что
![]() ,
,
![]() .
.
Лемма 1.1. Для любого целого р справедливо следующее соотношение
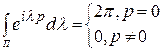 .
.
Доказательство.
Если ![]() , то доказательство очевидно. Рассмотрим случай
, то доказательство очевидно. Рассмотрим случай ![]() . Воспользуемся формулой Эйлера
. Воспользуемся формулой Эйлера
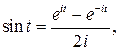
тогда
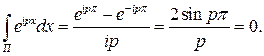
Лемма доказана.
Пусть ![]() - значения случайного процесса
- значения случайного процесса ![]() в точках
в точках ![]() . Введем функцию
. Введем функцию
![]() ,
,
которую будем называть характеристической функцией
, где ![]() - ненулевой действительный вектор,
- ненулевой действительный вектор, ![]() ,
, ![]() .
.
Смешанный момент ![]() го порядка
,
го порядка
, ![]() , можно также определить как
, можно также определить как
![]()
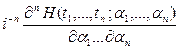
![]() ,
, ![]() ,
, ![]() .
.
Смешанным семиинвариантом (кумулянтом) ![]() го порядка
,
го порядка
, ![]() , случайного процесса
, случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
![]()
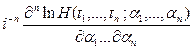
![]() ,
, ![]() ,
, ![]() ,
,
которую также будем обозначать как ![]() .
.
Между смешанными моментами и смешанными семиинвариантами ![]() го порядка,
го порядка, ![]() , существуют связывающие их соотношения, которые имеют вид
, существуют связывающие их соотношения, которые имеют вид
![]()
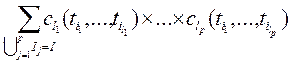 ,
,
![]()
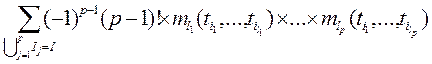 ,
,
где суммирование производится по всевозможным разбиениям множества
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При ![]()
![]() ,
,
![]() ,
,
![]() .
.
При ![]()
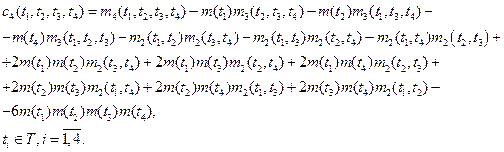
Спектральной плотностью
случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
![]() =
=![]()
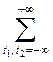
![]()
![]() ,
, ![]() ,
,
при условии, что
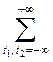
![]()
Из определения видно, что спектральная плотность ![]() непрерывная, периодическая функция с периодом, равным
непрерывная, периодическая функция с периодом, равным ![]() по каждому из аргументов.
по каждому из аргументов.
Семиинвариантной спектральной плотностью ![]() го порядка,
го порядка,
![]() , случайного процесса
, случайного процесса ![]() ,
, ![]() , называется функция вида
, называется функция вида
![]() =
=![]()
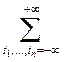
![]()
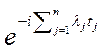 ,
, ![]() ,
,
при условии, что
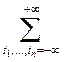
![]()
![]() .
.
Теорема 1.
Для смешанного семиинварианта ![]() го порядка,
го порядка, ![]() , случайного процесса
, случайного процесса ![]() справедливы представления
справедливы представления
![]()
![]()
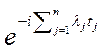
![]() ,
,![]() .
.
Пусть ![]() - случайный процесс, заданный на вероятностном пространстве
- случайный процесс, заданный на вероятностном пространстве ![]() , и
, и
![]()
![]() - мерная функция распределения, где
- мерная функция распределения, где ![]()
Случайный процесс ![]() называется стационарным в узком смысле
(строго стационарным), если для любого натурального
называется стационарным в узком смысле
(строго стационарным), если для любого натурального ![]() , любых
, любых ![]() и любого
и любого ![]() , такого что
, такого что ![]() выполняется соотношение
выполняется соотношение
![]()
где ![]()
Возьмем произвольное ![]() . Пусть
. Пусть ![]() , тогда
, тогда
![]()
В дальнейшем функцию, в правой части (1), будем обозначать
![]()
Используя определение стационарного в узком смысле СП ![]() , смешанный момент
, смешанный момент ![]() го порядка,
го порядка, ![]() , будем обозначать
, будем обозначать
![]()
![]()
Смешанный семиинвариант ![]() го порядка,
го порядка, ![]() , стационарного в узком смысле СП
, стационарного в узком смысле СП ![]() будем обозначать
будем обозначать
![]()
![]()
Случайный процесс ![]() , называется стационарным в широком смысле
, если
, называется стационарным в широком смысле
, если ![]() и
и
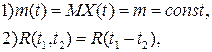
![]()
Замечание 1.
Если ![]() , является стационарным в узком смысле СП и
, является стационарным в узком смысле СП и ![]() то
то ![]() , является стационарным в широком смысле, но не наоборот.
, является стационарным в широком смысле, но не наоборот.
Спектральной плотностью
стационарного случайного процесса ![]() , называется функция вида
, называется функция вида
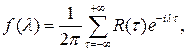
![]() ,
,
при условии, что
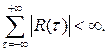
Семиинвариантной спектральной плотностью ![]() - го порядка
,
- го порядка
, ![]() , стационарного СП
, стационарного СП ![]() , называется функция вида
, называется функция вида
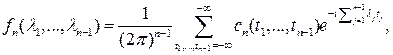
![]()
при условии, что
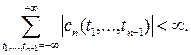
Для смешанного семиинварианта ![]() -го порядка,
-го порядка, ![]() , стационарного СП
, стационарного СП ![]() справедливо следующее соотношение
справедливо следующее соотношение
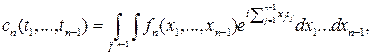
![]() .
.
Для ![]() эти соотношения примут вид
эти соотношения примут вид
![]()
![]() .
.
![]()
![]() 2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
Рассмотрим действительный стационарный в широком смысле случайный процесс![]()
![]() ,
,![]() , с математическим ожиданием
, с математическим ожиданием ![]() ,
, ![]() , взаимной ковариационной функцией
, взаимной ковариационной функцией ![]() , и взаимной спектральной плотностью
, и взаимной спектральной плотностью ![]() .
.
Предположим, имеются Т последовательных, полученных через равные промежутки времени наблюдений ![]()
![]() за составляющей
за составляющей ![]() , рассматриваемого процесса
, рассматриваемого процесса ![]() . Как оценку взаимной спектральной плотности в точке
. Как оценку взаимной спектральной плотности в точке ![]() рассмотрим статистику
рассмотрим статистику
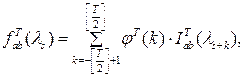 (2.1)
(2.1)
где ![]()
![]() , - произвольная, не зависящая от наблюдений четная целочисленная функция,
, - произвольная, не зависящая от наблюдений четная целочисленная функция, ![]() для
для 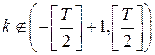 , а
, а
![]() (2.2)
(2.2)
s – целое число, 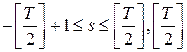 - целая часть числа
- целая часть числа ![]() .
.
Статистика ![]() , называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением
, называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением
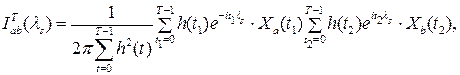 (2.3)
(2.3)
![]() определено равенством (2.2).
определено равенством (2.2).
Предположим, если оценка ![]() взаимной спектральной плотности
взаимной спектральной плотности ![]() , построенная по T наблюдениям, является асимптотически несмещенной, то математическое ожидание ее можно представить в виде
, построенная по T наблюдениям, является асимптотически несмещенной, то математическое ожидание ее можно представить в виде
![]() (2.4)
(2.4)
где ![]() некоторые действительные функции, не зависящие от T,
некоторые действительные функции, не зависящие от T, ![]()
В качестве оценки взаимной спектральной плотности возьмем статистику
![]() ,
,
и исследуем первый момент построенной оценки.
Математическое ожидание построенной оценки будет следующее
![]()
Использовав соотношение (2.4), получим
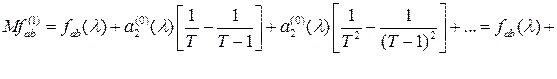
![]()
где
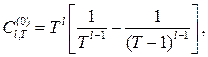
![]()
Поскольку
![]()
следовательно, оценка ![]() является асимптотически несмещенной со смещением, убывающим как
является асимптотически несмещенной со смещением, убывающим как ![]() .
.
Так как равенство (2.4) справедливо и при ![]() , то, рассматривая оценку
, то, рассматривая оценку
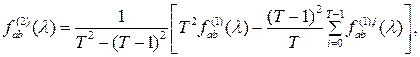
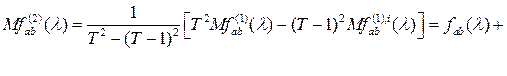
![]()
где
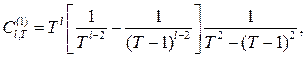
![]()
![]() , то оценка
, то оценка ![]() является асимптотически несмещенной со смещением, убывающим на
является асимптотически несмещенной со смещением, убывающим на ![]() . Далее рассмотрим оценку
. Далее рассмотрим оценку
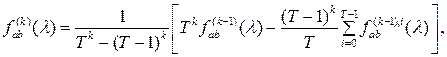 (2.5)
(2.5)
Найдем математическое ожидание построенной оценки :
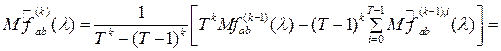
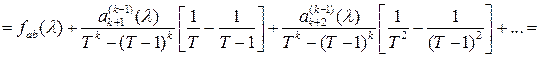
![]()
где
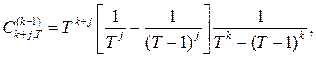
![]()
![]()
![]()
Следовательно, оценка ![]() является асимптотически несмещенной со смещением, убывающим как
является асимптотически несмещенной со смещением, убывающим как ![]() .
.
Найдем явный вид коэффициентов ![]() в представлении (2.4),
в представлении (2.4), ![]()
![]()
Видим, что
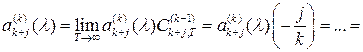
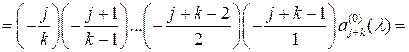
![]()
Таким образом, справедливо следующее утверждение.
Теорема 2.1
.
Оценка ![]() взаимной спектральной плотности
взаимной спектральной плотности ![]() стационарного в широком смысле случайного процесса
стационарного в широком смысле случайного процесса ![]() , задаваемая равенством (2.5), удовлетворяет соотношению
, задаваемая равенством (2.5), удовлетворяет соотношению
![]() ,
,
![]() ,
,
![]() при условии, что справедливо соотношение (2.4) для
при условии, что справедливо соотношение (2.4) для ![]()
При нахождении моментов оценок спектральных плотностей вторых и высших порядков появляются функции вида
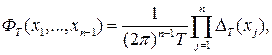 (2.6)
(2.6)
где ![]() задаются соотношением
задаются соотношением ![]()
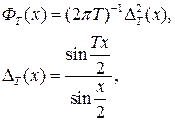
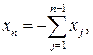
![]()
![]()
![]()
![]()
![]() 3. ОКНА ПРОСМОТРА ДАННЫХ
3. ОКНА ПРОСМОТРА ДАННЫХ
Чтобы выделить определенные характеристики спектральных оценок, нередко прибегают к сглаживанию значений на концах случайного временного ряда. Временное сглаживание представляет собой умножение ряда на «окно данных».
В соотношении (2.3) введена функция ![]() , называемая окном просмотра данных (множителем сходимости, коэффициентом сглаживания).
, называемая окном просмотра данных (множителем сходимости, коэффициентом сглаживания).
Функцию
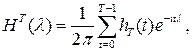 (3.1)
(3.1)
![]() называют частотным окном. Из соотношения (3.1) вытекает, что
называют частотным окном. Из соотношения (3.1) вытекает, что
![]()
Характерное поведение функции ![]() состоит в том, что она становится все более сконцентрированной в окрестности нуля при
состоит в том, что она становится все более сконцентрированной в окрестности нуля при ![]() .
.
Примеры окон просмотра данных:
1. 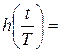 1 – окно Дирихле;
1 – окно Дирихле;
2. 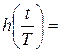 1-
1-![]() – окно Фейера;
– окно Фейера;
3. 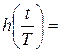
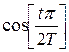 ;
;
4. 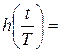
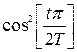 – окно Хэннинга;
– окно Хэннинга;
5. 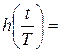
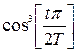 – окно Хэмминга;
– окно Хэмминга;
6. 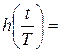
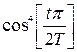 – окно Хэмминга;
– окно Хэмминга;
7. 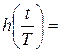
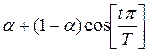 , где
, где ![]() – окно Хэмминга;
– окно Хэмминга;
8. 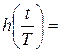 1-
1-![]() – окно Рисса.
– окно Рисса.
![]() ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
В данной работе исследована оценка спектральной плотности вида
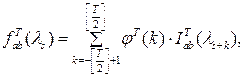
где ![]()
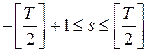 , а периодограмма задана следующим соотношением
, а периодограмма задана следующим соотношением
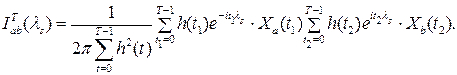
Построены графики этой оценки для различных окон данных на основании данных, представляющих собой последовательность наблюдений - температуры воздуха в городе Бресте с октября 2008 по февраль 2009 года.
Графики построены также для центрированного случайного процесса.
![]() СПИСОК
ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
СПИСОК
ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
1. Андерсон Т. Статистический анализ временных рядов. – М.: Мир, 1976. – 755 с.
2. Бриллинджер Д. Временные ряды. Обработка данных и теория. - М.: Мир, 1980. - 536 с.
3. Журбенко И.Г. Спектральный анализ временных рядов. - М.: Изд-во МГУ, 1982. - 168 с.
4. Труш Н.Н. Асимптотические методы статистического анализа временных рядов. – Мн.: БГУ, 1999. - 218 с.
5. Труш Н.Н., Мирская Е.И. Случайные процессы. Преобразования Фурье наблюдений. – Мн.: БГУ, 2000.
ПРИЛОЖЕНИЕ
Для исследования оценки (3.1) был исследован ряд, состоящий из 176 наблюдений ежедневной температуры воздуха в городе Бресте с октября 2008 по февраль 2009 года.
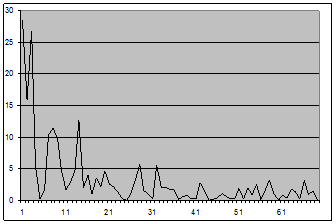
Рис. 1 - График оценки спектральной плотности (2.1) для окна Дирихле
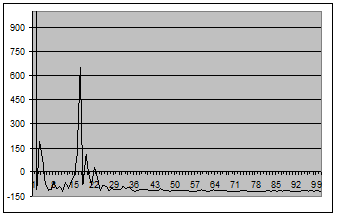
Рис. 2 - График оценки спектральной плотности (2.1) для окна Дирихле для центрированного случайного процесса
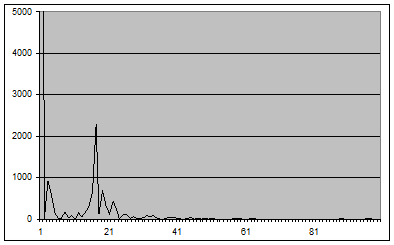
Рис. 3 - График оценки спектральной плотности (2.1) для окна Фейера
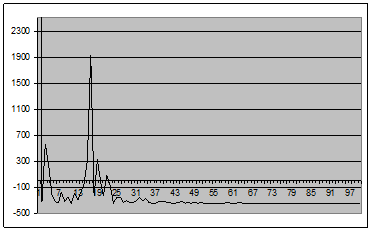
Рис. 4 - График оценки спектральной плотности (2.1) для окна Фейера для центрированного случайного процесса
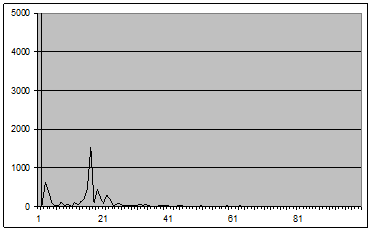
Рис. 5 - График оценки спектральной плотности (2.1) для окна вида 3
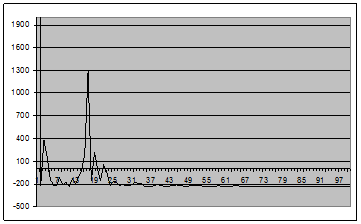
Рис. 6 - График оценки спектральной плотности (2.1) для окна вида 3 для центрированного случайного процесса
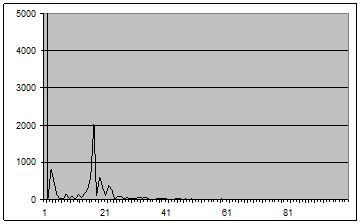
Рис. 7 - График оценки спектральной плотности (2.1) для окна Хэннинга
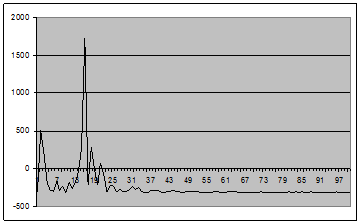
Рис. 8 - График оценки спектральной плотности (2.1) для окна Хэннинга для центрированного случайного процесса
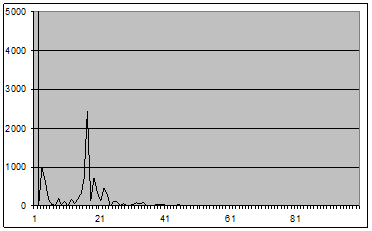
Рис. 9 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 5
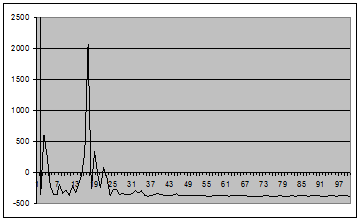
Рис. 10 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 5 для центрированного случайного процесса
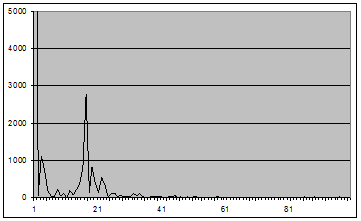
Рис. 11 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 6
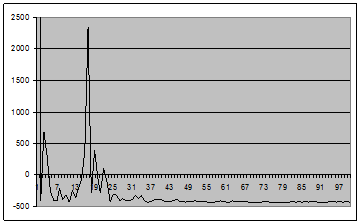
Рис. 12 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 6 для центрированного случайного процесса
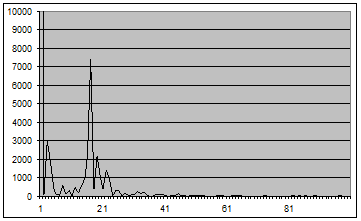
Рис. 13 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 7
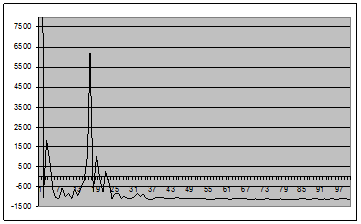
Рис. 14 - График оценки спектральной плотности (2.1) для окна Хэмминга вида 7 для центрированного случайного процесса
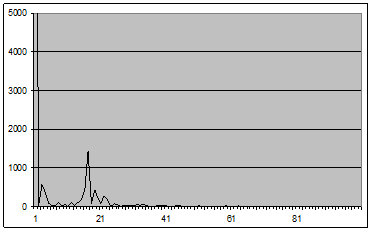
Рис. 15 - График оценки спектральной плотности (2.1) для окна Рисса
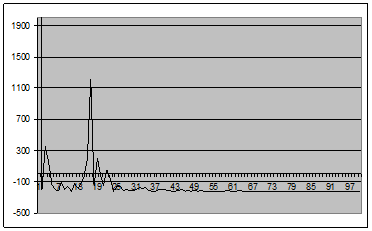
Рис. 16 - График оценки спектральной плотности (2.1) для окна Рисса для центрированного случайного процесса
Похожие работы
-
Математические модели окружающей среды
Расчет моментов ряда, построение функции распределения и плотности функции распределения, ее аппроксимация теоретическими зависимостями. Определение стационарности ряда. Вычисление куммулятивной частоты превышения уровня. Прогноз превышения уровня.
-
Роль прикладной математики в подготовке учителей математики и информатики
В статье обсуждаются вопросы вузовской подготовки учителей математики и информатики по дисциплинам прикладной математики. Приводятся примеры изучения дисциплин прикладной математики с точки зрения особенностей конкретного профиля подготовки студентов.
-
Теорема Котельникова
Для того, чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми искажениями (погрешностями), необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании аналогового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации
-
Случайные процессы
Оглавление Случайная функция, случайный процесс, случайное поле 3 Функция распределения вероятностей случайного процесса 5 Плотность распределения вероятностей случайного процесса 7
-
Понятие случайного процесса в математике
Определение случайного процесса в математике, ряд терминов и понятий, описывающих механизм этого процесса. Марковские, стационарные случайные процессы с дискретными состояниями. Особенности эргодического свойства стационарных случайных процессов.
-
Случайные функции
Случайные процессы в системах автоматического регулирования.
-
Оценивание смещения статистики взаимной спектральной плотности многомерного временного ряда
Математический факультет Кафедра информатики и прикладной математики Курсовая работа НА ТЕМУ: «ОЦЕНИВАНИЕ СМЕЩЕНИЯ СТАТИСТИКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МНОГОМЕРНОГО ВРЕМЕННОГО РЯДА»
-
Теория вероятности
Формулировка теоремы Бернулли, проверка ее с помощью программы. Моделирование случайной величины методом кусочной аппроксимации. График распределения Коши, построение гистограммы и нахождения числовых характеристик, составление статистического ряда.
-
Расчет стационарного токораспределения в условиях смешанной кинетики
Рассматривается математическая модель стационарного электрического поля в электрохимической системе с учетом омического падения потенциала в электролите и концентрационных ограничений в приэлектродных диффузионных слоях.
-
Спектральный анализ сигналов электрооптического рассеяния света в аэродисперсной среде
Статистический анализ токового сигнала позволяет дать объективную количественную оценку характеристик электрооптического светорассеяния и существенно расширяет возможности исследователя.