Название: Контрольная работа по Экономико-математическим методам

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 75.43 Kb

Скачать файл: referat.me-218401.docx

Краткое описание работы: Контрольная работа по дисциплине «ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ и модели» вариант 10 Алгоритм решения транспортной задачи Применение алгоритма решения транспортной задачи требует соблюдения ряда предпосылок:

Контрольная работа по Экономико-математическим методам

Контрольная работа по дисциплине

«ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ и модели»

вариант 10

Алгоритм решения транспортной задачи

Применение алгоритма решения транспортной задачи требует соблюдения ряда предпосылок:

1. Должна быть известна стоимость перевозки единицы продукта из каждого пункта производства в каждый пункт назначения.

2. Запас продуктов в каждом пункте производства должен быть известен.

3. Потребности в продуктах в каждом пункте потребления должны быть известны.

4. Общее предложение должно быть равно общему спросу.

Алгоритм решения транспортной задачи состоит из четырех этапов:

Этап 1. Представление данных в форме стандартной таблицы и поиск любого допустимого распределения ресурсов. Допустимым называется такое распределение ресурсов, которое позволяет удовлетворить весь спрос в пунктах назначения и вывезти весь запас продуктов из пунктов производства.

Этап 2. Проверка полученного распределения ресурсов на оптимальность

Этап 3. Если полученное распределение ресурсов не является оптимальным, то ресурсы перераспределяются, снижая стоимость транспортировки.

Этап 4. Повторная проверка оптимальности полученного распределения ресурсов.

Данный итеративный процесс повторяется до тех пор, пока не будет получено оптимальное решение.

Широко распространенным методом решения транспортных задач является метод потенциалов.

Если допустимое решение , i=1,2,…,m; j=1,2,…n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков i=1,2,…,m и потребителей j=1,2,…,n, удовлетворяющее следующим образом:

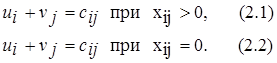
Группа равенств (2.1) используется как система уравнений для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных i=1,2,…,m и j=1,2,…,n. Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n-1. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы.

Группа неравенств (2.2) используется для проверки оптимальности опорного решения. Эти неравенства удобнее представить в следующем виде:

(2.3)

Числа называются оценками для свободных клеток таблицы (векторов условий) транспортной задачи.

Опорное решение является оптимальным, если для всех векторов условий (клеток таблицы) оценки неположительные.

Оценки для свободных клеток транспортной таблицы используются при улучшении опорного решения. Для этого находят клетку (l,k) таблицы, соответствующую . Если , то решение оптимальное. Если же , то для соответствующей клетки (l,k) строят цикл и улучшаю решение, перераспределяют груз

по этому циклу.

Алгоритм решения транспортных задач методом потенциалов:

1. Проверить выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводится фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок.

2. Построить начальное опорное решение (методом минимальной стоимости или каким-либо другим методом), проверить правильность его построения по количеству занятых клеток (их должно быть m+n-1) и убедиться в линейной независимости векторов условий (используется метод вычеркивания).

3. Построить систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений:

которая имеет бесконечное множество решений. Для нахождения частного решения системы одному из потенциалов (обычно тому, которому соответствует большее число занятых клеток) задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяются по формулам:

если известен потенциал , и

если известен потенциал

4. Проверить выполнения условия оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам

и те из них, которые больше нуля, записываются в левые нижние углы клеток. Если для всех свободных клеток , то вычисляют значение целевой функции и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, опорное решение не является оптимальным.

5. Перейти к опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка

Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину . Клетка со знаком «-», в которой достигается остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным .

Далее перейти к пункту 3 данного алгоритма.

Контрольная задача 1

Предприятие выпускает продукцию А, Б, и В. Каждый вид продукции может производиться различными технологическими способами (на разном оборудовании, с использованием различного сырья, при разной квалификации рабочих).

Ресурсы оборудования, сырья, труда ограничены:

Оборудование, станко-час.		Сырье, т		Труд, чел.-час.
новое	старое	высококач.	стандарт.	высококвалиф.	ср. квалиф.
161000	401000	71000	41000	220000	160000

Выпуск продукции А, Б и В не может быть меньше заключенных на эту продукцию договоров:

Продукция
А	Б	В
5400	2050	4000

Нормативы затрат ресурсов на производство продукции и прибыль при использовании различных технологических способов в расчёте на единицу продукции:

Наименование ресурсов	Ед.изм.	Продукция А		Продукция Б		Продукция В
		технологич. способы		технологич. способы		техн. способы
		1	2	1	2	1	2	3
Оборудование:	станко-час.
новое	10	-	20	-	30	32	-
старое	-	12	-	25	-	-	40
Сырье:	т
высококачественное	2	-	5	-	10	10	-
стандартное	-	2	-	5	-	-	9
Труд:	чел.-час.
высококвалифицированный	18	-	30	-	40	-	-
средней квалификации	-	20	-	32	48	50
Прибыль	т.руб.	300	500	350	700	720	1200	1300

Требуется определить оптимальный план производства продукции, который приносил бы максимальная прибыль.

Решение

Решим данную задачу в среде EXCEL.

Для этого создадим форму и введем исходные данные.

При помощи команды Поиск решений найдем план производства удовлетворяющий ограничениям задачи и приносящий максимальную прибыль.

Исходя из решения задачи можно сделать вывод, что для получения максимальной прибыли предприятию необходимо выпускать продукцию в следующих объемах:

Продукция А технологическим способом 1 – 1143 ед.,

Продукция А технологическим способом 2 – 4257 ед.,

Продукция Б технологическим способом 2 – 2050 ед.,

Продукция В технологическим способом 1 – 4986 ед.,

Продукция В технологическим способом 3 – 185 ед.

При этом прибыль предприятия составит 7736829 тыс. руб.

Следует заметить, что некоторые ресурсы остаются недоиспользованными, а именно:

оборудование старое – на 291258 станко-час.,

сырье высококачественное – на 18857 т.,

сырье стандартное – 20569 т.

Контрольная задача 2

Четыре оптовых склада обслуживают четыре магазина одним товаром.

Исходные данные:

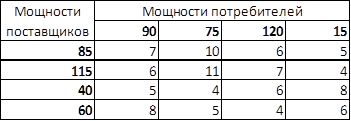
Необходимо составить оптимальный план перевозок, который имел бы минимальную стоимость.

Решение

Решим данную задачу в среде EXCEL.

Для этого создадим форму и введем исходные данные.

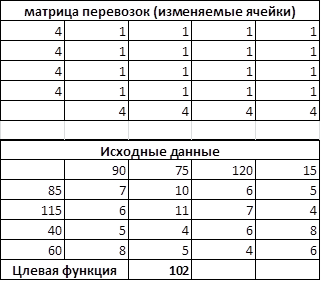
При помощи команды Поиск решений найдем план перевозок, удовлетворяющий условиям задачи и имеющий минимальную стоимость.

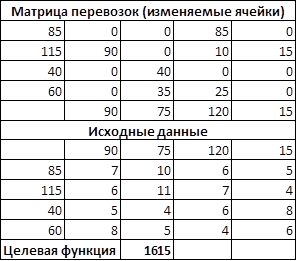
Исходя из решения задачи можно сделать вывод, что для минимизации расходов на перевозку товара необходимо:

С 1-го склада отправить весь товар в 3-ий магазин в количестве 85 ед.,

Со 2-го склада отправить в 1-ый магазин 90 ед. товара, в 3-ий магазин – 10 ед., в 4-ый магазин – 15 ед.,

С 3-его склада отправить весь товар во 2-ой магазин в кол-ве 40 ед.,

С 3-го склада отправить во 2-ой магазин 35 ед. товара, в 3-ий магазин – 25 ед. товара.

При этом стоимость перевозки составит 1615 тыс. руб.