Название: Перестановки

Вид работы: реферат

Рубрика: Математика

Размер файла: 42.78 Kb

Скачать файл: referat.me-218813.docx

Краткое описание работы: Описываются понятия r-перестановок множества, r-сочетания, перестановки с повторениями.

Перестановки

Описываются понятия r-перестановок множества, r-сочетания, перестановки с повторениями.

п.1. r- перестановки.

Определение. r- перестановкой множества A называется кортеж из r попарно различных элементов множества A. Иногда r- перестановки называют размещениями без повторения.

Если (a, ..., a) есть r- перестановка n- элементного множества, то r £ n.

Обозначение. Обозначим P(n, r) число всех r- перестановок n- элементного множества, где n, rÎN. Положим P(n, 0) = 1 для nÎN0.

Теорема 1. Число всех r- перестановок n- элементного множества, где

n, rÎN, вычисляется по формуле

P(n, r) = n= n(n -1)...(n - r + 1). (1)

Доказательство. Первая координата r- перестановки n- элементного множества может быть выбрана n способами, если первая координата выбрана, то вторая координата может быть выбрана n-1 способами, если выбраны первые две координаты, то третья координата может быть выбрана n-2 способами и т.д. до r- ой координаты включительно, которая может быть выбрана n-r+1 способами. Из теоремы 2, п.3, следует равенство (1).

Следствие 1. Пусть A и B- конечные множества, |A| = n, |B| = r, где

n, r ÎN. Тогда число всех инъекций f: B ® A равно P(n, r) = n.

Доказательство. Обозначим B={b, ..., b}, инъекция f: B ®A может быть записана в табличной форме

,

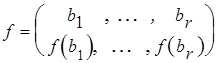где кортеж есть r- перестановка множества A. Поэтому искомое число равно P(n, r).

Определение. Пусть A есть n- элементное множество. Перестановкой множества A называется n- перестановка множества A. Другими словами, перестановка множества A это кортеж содержащий все элементы множества A по одному разу.

Следствие 2. Число всех перестановок n- элементного множества равно n!.

Доказательство. Искомое число равно P(n, n) = n= n(n-1)...(n-n+1) =

= n!.

Следствие 3. Пусть A и B- конечные множества, |A| = |B| = n, nÎN. Тогда число всех биекций f: B ® A равно n!.

Доказательство. Т.к. |A| = |B|, то каждая биекция f: B ® A является инъекцией и наоборот. По следствию 1, искомое число равно P(n, n) = n!.

п.2. r -элементные подмножества (r - сочетания).

Определение. Пусть A- конечное множество. r- сочетанием множества A называется любое r- элементное подмножество множества A.

Теорема 1. Пусть A есть n- элементное множество, n, rÎN. Справедливы утверждения:

1. Число всех r- сочетаний n- элементного множества равно .

2. Число всех r- элементных подмножеств n- элементного множества равно .

Доказательство. Обозначим K- число всех r- сочетаний n- элементного множества A. Каждое r- элементное подмножество n- элементного множества A определяет r! перестановок множества A, при этом разные подмножества определяют разные перестановки. Поэтому K×r! - число всех r- перестановок множества A, равное n. Отсюда следует, что K = n/ r! = =.

Пример 1. Каждый кортеж N, где , кодируется k-элементным подмножеством множества . Поэтому, при фиксированном k, число всех кортежей N, где , равно .

Пример 2. Перечисление беспорядков степени n. Обозначим U- множество всех перестановок степени n, . Будем считать, что элементами перестановок являются числа . Перестановка степени n называется беспорядком, если для всех .

Существует только один беспорядок степени 2.

Существует только два беспорядка степени 3.

Для обозначим множество всех перестановок степени n таких, что . Число всех беспорядков степени n равно числу всех перестановок степени n не принадлежащих множеству . Обозначим число всех беспорядков степени n. По формуле включения- исключения

, (1)

где суммирование ведётся по всем кортежам Nтаким, что

. Легко видеть, что для любого кортежа N, где справедливо равенство

.

При фиксированном k число всех кортежей N, где , равно . Из равенства (1) следует, что

.

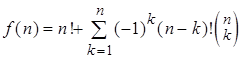Поэтому

.

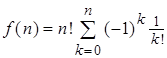п.3. Перестановки с повторениями.

Определение. Кортеж t = (b, ..., b) называется перестановкой с повторениями состава (n, ..., n) множества {a, ..., a}, если элемент a входит в t n раз, ..., a входит в t n раз, где n, ..., nÎN, .

Обозначение. Обозначим P(n, ..., n) число всех перестановок с повторениями состава (n, ..., n) некоторого k - элементного множества, где n = = n+...+n.

Теорема 1. Для любого (n, ..., n)ÎN

P(n, ..., n) = n!/n!...n! , где n = n+...+n .

Доказательство. Перестановка (b, ..., b) состава (n, ..., n) множества {a, ..., a} кодируется кортежем длины k: на первом месте кортежа записано множество тех мест в перестановке на которых расположен элемент ; на втором месте кортежа записано множество тех мест в перестановке, на которых расположен элемент ; ...; на k - ом месте кортежа записано множество тех мест в перестановке, на которых расположен элемент . Первый элемент кортежа может быть выбран способами; если первый элемент выбран, то второй можно выбрать 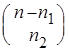способами; ...; если первые элементов выбраны, то k- ый элемент может быть выбран 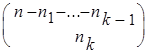способами. По правилу произведения получаем, что число всех перестановок с повторениями состава (n, ..., n) из {a, ..., a} равно

P(n, ..., n) = ...=

=

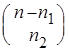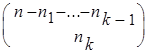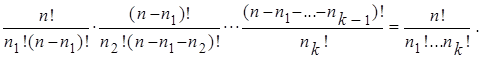
Обозначение. Для " n, ..., nÎN полиномиальный коэффициент 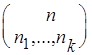определяется равенствами:

если n +...+ n = n, то ;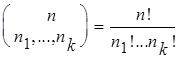

если n +...+ n¹ n, то .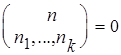

Следствие 1. Пусть A и B- конечные множества такие, что |A| = n, |B| = k, (n, ..., n)ÎN, n +...+ n = n, B = {b, ..., b}. Тогда число всех функций

f:A®B таких, что |f (b)| = n для всех i = 1, ..., k, равно .

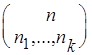Доказательство. Пусть A={a, ..., a}. Запишем функцию f:A®B в табличном виде .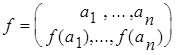

Кортеж (f(a), ..., f(a)) есть перестановка с повторениями состава (n, ..., n) множества {b, ..., b}.

Следствие 2. Пусть U- конечное множество, |U| = n. Тогда число кортежей множеств (A, ..., A) таких, что

|A| = n, ..., |A| = n,

|AÇA| = Æ для всех i ¹ j,

AÈ...ÈA = U, равно.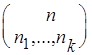

Доказательство. По теореме 2 п.3 число таких кортежей равно

...= .

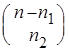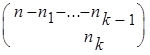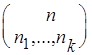Список литературы

Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002

В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.

Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000

Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000

Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000

Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001