Название: Дискретный анализ

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 52.89 Kb

Скачать файл: referat.me-215617.docx

Краткое описание работы: Классическая задача комбинаторики, ее решение "правилом произведения". Реализация реальных связей между объектами в математических терминах на абстрактных множествах. Решение задач на доказательство тождества, особенности решения системы уравнений.

Дискретный анализ

Содержание

Введение

1.Сколькими способами можно выбрать гласную и согласную буквы из слова «полка»

2.Решить систему уравнений:

3.Решить уравнение:

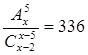
4.Доказать тождество:

Ø

5.Перечислить элементы множеств AxB и BxA, если , а

6.Упростить выражение

Введение

Основные способы представления информации называются дискретными: это слова и конструкции языков и грамматик – природных и формализованных; табличные массивы реальных данных в технических системах и научно-природных наблюдений; данные хозяйственной, социальной, демографической, исторической статистики и т.п.

Для количественного анализа и вычисления превращений непрерывных процессов приходится их "дискретизировать". Понятно, что математические методы обработки, анализа и превращений дискретной информации необходимы во всех отраслях научной, хозяйственной и социальной сферах. Обычно эти методы изучаются на курсах дискретной математики; иногда применяется определение "конечная математика", или даже "конкретная математика".

Часто для анализа реальных систем с непрерывными конструктивными элементами строятся модели конечной или дискретной математики. Например, классическая транспортная или информационная сеть трактуется как граф с заданными пропускными способностями или массами веток, а геометрическая форма ветки между двумя пунктами-узлами сети не играет роли. Более того, "непрерывное" строение реальной ветки также не работает в сетевой модели: важно, что между двумя узлами а, b сети или нет ветки, или есть ветка с заданными ограничениями c(a, b) объема переноса веществ или информации. В модели хватит задать числа c(a, b) для каждой пары узлов a, b. Если ветки нет, то c(a, b)=0. Такая числовая модель отображения сети идеальна для записи, сохранения и превращений в компьютере.

1.Сколькими способами можно выбрать гласную и согласную буквы из слова «полка»

Решение

Эта задача представляет собой вид классической задачи комбинаторики. Ее разрешение сводится к "правилу произведения". Исходя из которого, если М₁ , М₂ , М₃ , …, М_k – конечные множества и М = М₁ х М₂ х М₃ х … х М_k – их декартовое произведение, то

(1)

Пусть предмет а₁ можно выбрать m₁ способами, предмет а₂ – m₂ способами, …, предмет а_k – m_k способами и пусть выбор предмета а₁ не влияет на количество способов выбора предметов а₂ , …, а_k ; и т.д. Тогда выбор упорядоченного множества предметов (а₁ , а₂ , …, а_k ) в указанном порядке можно выполнить способами.

(2)

Отсюда – если нам необходимо подсчитать сколькими способами можно выбрать гласную и согласную буквы из слова "полка", то сначала выберем гласную – это можно сделать 2 способами (так как их две), после этого каждой гласной добавим согласную (аналогично 3 способа). По правилу произведения выбор упорядоченного множества гласной и согласной букв составит:

Ответ. n = 6.

2.Решить систему уравнений:

Решение

1.Найдем n из формулы дискретного соединения:

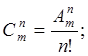(3)

Из нижеследующего доказательства следует, что:

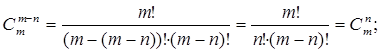(4)

Таким образом:

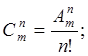
Следовательно .

Подставив значение в формулу дискретной перестановки 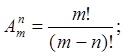(5),

(5)

получим:

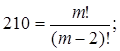
Сократим m! и (m-2)!:

Решив квадратное уравнение, найдем один подходящий корень .

Проверим правильность решения:

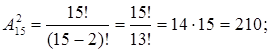
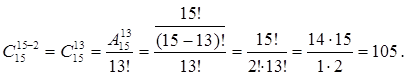
Ответ: , .

3.Решить уравнение:

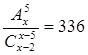
Решение

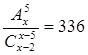
Используя формулы дискретной перестановки (5) и соединения (3), получим:

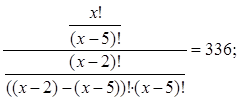
Упростим выражение:

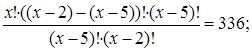
Используя сокращение, получим:

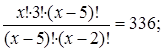
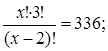
Расписав факториал, получим:

Решим квадратное уравнение:

Ответ:

4.Доказать тождество:

Ø

Решение

Раскроем пары скобок (первое и второе пересечения, третье и четвертое):

Сократим выражение:

Раскроем скобки:

Сократим выражение:

5.Перечислить элементы множеств AxB и BxA, если , а

Решение

Отношения реализуют в математических терминах на абстрактных множествах реальные связи между реальными объектами. Отношения применяют при построении компьютерных баз данных, которые организованы в виде таблиц данных. Связи между группами данных в таблицах описывают языком отношений. Именно данные обрабатываются и превращаются при помощи операций, математически точно определенных для отношений. Такие базы данных называют реляционными и широко используют для сохранения и обработки различной информации: производственной, коммерческой, статической и т.п. Отношения также часто используют в программировании. Такие составляющие структуры данных, как списки, деревья и т.п. обычно используют для описания какого либо множества данных вместе с отношением между элементами этого множества.

Декартовым произведением множеств Х1 х Х2 х … х ХN, называется множество всех возможных упорядоченных наборов (х₁ , х₂ , …, х_n ) с n элементов (которые называют кортежами длины n), в которых первый элемент принадлежит множеству Х1, второй – множеству Х2, n-й – множеству Хn. Декартовое произведение Х х Х х … х Х, в котором одно и то же множество Х умножается n раз само на себя, называют декартовой степенью множества и обозначают Хⁿ . При этом Х¹ = Х. Множество Х² называют декартовым квадратом множества Х, множество Х³ называют декартовым кубом множества Х.

Таким образом, если , а , то:

а)

б) .

Ответ:

, .

6.Упростить выражение

Решение

а) упростим левую часть выражения:

б) упростим правую часть выражения:

в) объединив полученный результат, получим:

Ответ: .