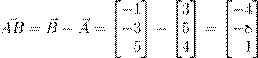Название: Решения с подробным описанием Векторы
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 102.52 Kb
Скачать файл: referat.me-218828.pdf
Краткое описание работы: Çàäà÷à 1. Äàíû âåêòîðû a = 3i + j è b = 2i + 3j.
Решения с подробным описанием Векторы
˙ 1. ˜ ß Œ ß a = 3i + j Ł b = 2i + 3j .
(a) ˇ æ Ł Œ Ł Ł Ø ºŁ ß ª º Ł , Ł a .
(b) ˇ æ Ł Œ a/ 2 − b .
— ł Ł :
(a) ¯æºŁ a - Œ , |a | - ºŁ Œ a , ºŁ Œ a/ |a | Ł Ł ,
Ł æ√ º √æ a
. ˜ºŁ Œ Œ Ł æ ß Œ Œ Ł :
|a | = 32 + 12 = 10, ŁæŒ ßØ Œ
(b)
˙ 2. ˜ ß Œ
.
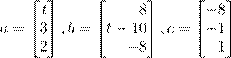˝ Ø æ Ł t , Ł Œ ßı
(a) ´ Œ a Ł b Œ ººŁ ß.
(b) ´ Œ a Ł c ŁŒ º ß.
(c) ´ Œ a , b Ł c Œ º ß.
(d) ´ Œ a , b Ł c Æ ßØ Æ Łæ.
— ł Ł :
(a) ´ Œ a Ł b Œ ººŁ ß ª Ł º Œ ª , Œ ª Łı Œ Ł ß Ł º ß.
ˇ æŒ º Œ ł Ł æº Łı Œ Ł -4, ŒŁ º Æß Ł ł Ł ßı Ł ßı Œ Ł :
8/t = −4 ⇐⇒ t = −2, (−2 − 10)/ 3 = −4.
(b) ´ Œ a Ł c ŁŒ º ß ª Ł º Œ ª , Œ ª Łı æŒ º
Ł 0. Œ º Ł Ł ( æ ßı Ł ŁØ
Ł … ßı Œ Ł ):
(a,b ) = −8t − 3 + 2 = −8t − 1 = 0 ⇐⇒ t = −1/ 8.
(c) ´ Œ a , b Ł c Œ º ß ª Ł º Œ ª , Œ ª ºŁ º Ł ß,
— æ º ß º Ł t = 4 ŁºŁ t = −2.
(d) ´ Œ a , b Ł c Æ ßØ Æ Łæ ª Ł º Œ ª , Œ ª ºŁ º Ł ß, æ æ º Ø Ł Œ Ł Œ Œ Łı æº Ł º Ł º .
ºŁ º æ Ł ß ø Œ Ł (t −4)(t +2).
ß Ł º Ł º Ł t < −2 ŁºŁ t > 4.
˙ 3. ˜ºŁ Œ a , |a | = 2. ˜ºŁ Œ b , |b | = 3. ª º
Œ Ł a Ł b , ϕ = 60◦ . ˝ Ø Ł
(a) ˜ºŁ ß Ł ª º Ø ºº º ª , æ ª Œ ı a Ł b . (b) ˇº ø ºº º ª , æ ª Œ ı 2a − b Ł a + 3b . — ł Ł :
| (a) ˜Ł ª ºŁ | ºº º ª , æ ª | Œ | ı a Ł b , | Œ |
| Ł | Łæ Œ Œ a − b Ł a + b . | ˜ºŁ | Œ | æ Ł |
| Œ Œ Œ | ßØ Œ Ł ª æŒ º ª | Ł | Ł æ Æ . | Œ º |
| Ł Ł | ı Œ æ Ł | Œ Œ | Ł Ł | Łı ºŁ |
| Œ æŁ æ ªº | Ł Ł, æŒ º | Ł | Ł Ł ª | º Ø ºº º ª |
| æ Æ | æ Ł ŒŁ Æ : |
,
√ 
√
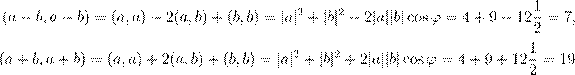ºŁ ß Ł ª º Ø ß 7 Ł 19.
(b) ˇº ø ºº º ª , ª 2 Œ , ºŁ Œ ª Ł Ł Łı ı Œ . ´ Œ Ł Ł ı Œ
º Ł Ł Łı ºŁ æŁ æ ªº Ł Ł,
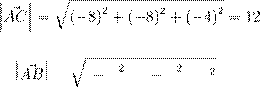
º Ł ŁŒ º Ł Æ Ł Ł Æ æ Ł Ł ØŒ Œ , :
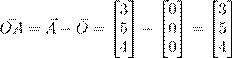
| ˙ 4. ˜ ß | ŒŁ A (3, 5, 4), B (−1, −3, 5), C (−5, −3, 0) Ł O (0, 0, 0). | |||||
| (a) ˝ Ø Ł Œ æŁ | æ ª º Œ Ł AB Ł AC . | |||||
| (b) ˝ Ø Ł º ø | 4ABC . | |||||
| (c) ˝ Ø Ł Æœ… | ª º Ø Ł Ł ß OABC . | |||||
| (d) ˝ Ø Ł ºŁ | ßæ ß Ł Ł ß, ø Ø Ł łŁ ß O . | |||||
— ł (a) |
Ł : | −5 3 −8 AC~ = C~ − A~ = −3 − 5 = −8 0 4 −4 −1 3 −4 AB~ = B~ − A~ = −3 − 5 = −8 5 4 1 |
||||
| ª | Ł | æŒ Ø ŒŁ Ł æŒ º Ł | Ł | ı | Œ | |
| Ł | Ł Łı ºŁ Œ æŁ æ ªº Œ | Ł. | ||||
| ˜ºŁ a | Œ | |||||
.
˜ºŁ a Œ
Œ º ß Ł Ł ı Œ º æ Łæº , æ ßı
Ł ŁØ Ł … ßı Œ Ł .
Œ º Ł Ł Œ
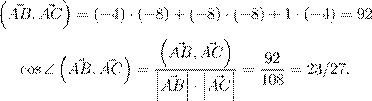
3
| (b) ´ Œ oe Ł Ł ı Œ º æ Œ | o , ºŁ | Œ | ª | |||
| º ø Ł ºº º ª , ª ß | . | |||||
Œ Œ Œ 2 Œ æ ºº º ª Ł ª º ø Æ 2 ł , Œ æ |
ª º | ŁŒ, | ||||
| º Ł | ºŁ ß | Œ ª Ł Ł æ ª º | ŁŒ . | |||
| ˇ æ Ł | Œ Ł Ł æ : −5 3 −8 AC~ = C~ − A~ = −3 − 5 = −8 0 4 −4 −1 3 −4 AB~ = B~ − A~ = −3 − 5 = −8 5 4 1 |
|||||
| ´ß ŁæºŁ | Œ | Ł Ł …ı æ | æ | , | æ Ł | |
| æ | ºŁ | º Ł ß, Œ Ø Ø æ Œ æ | Œ | Ł | ß | |
| ß, | Ø Ł Ø - Œ Ł ß ª Ł ª Œ | æ | æ | . | ||
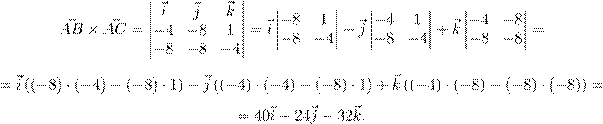
˜ºŁ a Œ
.
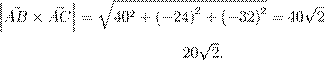˛ æ º ø ª º ŁŒ
| (c) ł ß Ł | Ł …ı Œ º æ | Łæº , º |
| Æœ… ºº º Ł | , ª Ł Ł | Œ . ˙ Œ Łæº "+", |
| æºŁ Ł Ł Œ | Æ ØŒ Œ | , Ł " ", æºŁ º . |
| ˛Æœ… ºº º | Ł Ł æ Ł | Œ Œ º ø æ Ł , |
| ºŁ | ßæ ß. ˝ Ł Œ | æ ºº º Ł |
| ª º Ł Ł . Ł | Ł ß Æœ… æ æ º 1/3 | |
| º ø Ł æ Ł | Ł Ł ß, Ø | ßæ Ł Ł ß. ´ Ø |
| æŁ ŁŁ ºŁ ß ßæ | Ł Ł ß Ł ºº º Ł | ß, æ Ł Ł Ł ß |
| º ø Ł 2 | ł ( ª º ŁŒ º Ł | ºº º ª ). ˇ |
| Æœ… Ł Ł ß Æ | 6 ł Æœ… æ | æ ø ª ºº º Ł . |
| ˇ º ı | Ł Æœ… Ł Ł ß æ | ºŁ 6 º |
| æ ł ª Ł | Ł …ı Œ Ł Ø … łŁ ß æ º ß . −5 0 −5 |
|
OC~ = C~ − O~ = −3 − 0 = −3
0 0 0
−1 0 −1
OB~ = B~ − O~ = −3 − 0 = −3
5 0 5
3 0 3
OA~ = A~ − O~ = 5 − 0 = 5 4 0 4
´ß ŁæºŁ æ ł Ł Ł …ı Œ , æ Ł ºŁ º Ł ß, Œ Ø Ø æ Œ æ Œ Ł ß ª Œ , Ø ª , Ø - Œ Ł ß ª Œ .
ˇ æ Ł ºŁ º æ æ ø Ø Ł ß:
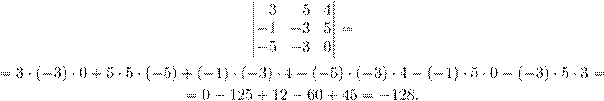
ˇ æ ł Ł Ł (OA,~ OB,~ OC~ ) = −128. ˛ æ Æœ… Ł Ł ß
64/ 3.
| (d) | Æß Ø Ł | ºŁ ßæ | ß | Ł | Ł | , | ø | Ø Ł | łŁ ß O æ |
| æ | Œ Ł | Œ |
| Œ , | ŁŒ º ßØ æ Ł , Œ æŒ æ ßæ , ŁºŁ |
| Œ | ºŁ Œ º æŒ æ Ł, ı ø Ø æ Ł . æ Ł æ |
| Œ. — ææ | Ł Œ
|
| Ł |  |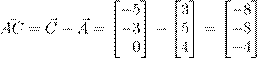
| Æß º | Ł Œ ºŁ ( ŁŒ º ßØ) Œ º æŒ æ Ł, ı ø Ø |
| Ł | ŒŁ, Œ , º øŁ Ø º æŒ æ Ł Ł Łı |
| Œ | Ł Ł . |
| ´ Œ ß | Ł Ł ı Œ º æ ŁØ Œ , º ßØ |
| ŁŒ º | Æ Ł Œ Ł Æ øŁØ æ Ł Ł ØŒ Œ . |
| ´ß ŁæºŁ | Œ Ł Ł …ı æ æ , æ Ł |
| æ | ºŁ º Ł ß, Œ Ø Ø æ Œ æ Œ Ł ß |
| ß, | Ø Ł Ø - Œ Ł ß ª Ł ª Œ æ æ . |
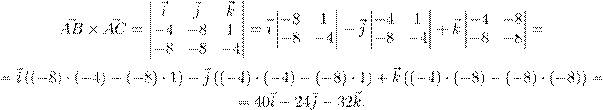
˛ Ł ª Ł æŒŁı Ł ŁØ æŒ º ª Ł Ł ı Œ
| Œº | æ , ª º | ºŁ | ª | Œ | , | Ø |
| ºŁ | Œ ŁŁ ª ª Œ | . ˛ æ | º | , | Æß | |
| ºŁ | Œ ŁŁ, º æŒ º | ª Ł | Ł | ºŁ | ºŁ | |
| Œ , | Œ ßØ Łæı Ł | Œ Ł . | ||||
| Œ º | ß Ł Ł ı | Œ º | æ | Łæº , | æ | ßı |
| Ł | ŁØ Ł … ßı Œ Ł | . | ||||
| Œ º | Ł Ł Œ |
5
˜ºŁ a Œ
.
˜ºŁ Œ ŁŁ Œ OA ~ Œ AB ~ × AC ~ :
.
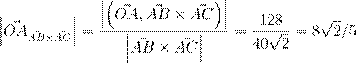˙ 5. ˜ ß Œ
.
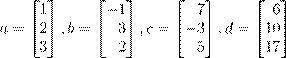(a) ˜ Œ , Œ ß a , b Ł c Æ Æ Łæ. (b) ˝ Ø Ł Œ Ł ß Œ d Æ Łæ .
— ł Ł :
(a) ØŒ Œ æ æ IR3 Æ Æ Łæ ª Ł º Œ ª , Œ ª
ºŁ º Ł ß, æ æ º Ø Ł Œ Ł Łı Œ ,
º .
(b) Æß Ø Ł Œ Ł ß Œ d Æ Łæ , Æı Ł Ø Ł ŒŁ ø æ ß Łæº x 1 , x 2 Ł x 3 , ax 1 + bx 2 + cx 3 = d , Ł ª ,
| łŁ | æŁæ | ŁØ 1 − x 2 + 7x 3 = 6 x 2x 1 + 3x 2 − 3x 3 = 10 . 3x 1 − 2x 2 + 5x 3 = 17 |
|||
| — æłŁ | Ø | Ł | Ø Ø æŁæ ß ŁØ | º | æ |
.
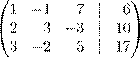| ˝ | Ł | Ł : | º | ı | Ł ł | Ł æŁæ | ß ºŁ Ø ßı | ŁØ æ |
| Ø | æłŁ | Ø | Ł | Ø æº | æº | ª º | ß | |
| Æ | Ł | æ | Œ | Ł. ˇ Ł | æ | ł ŁØ æŁæ | ŁØ, | |
| æ | æ | øŁı | Ł | Ł Ł | º | ª Æ | Ł Ł æº | |
| - æ | . | |||||||
| º | ß | Æ | Ł æ | Œ Ł | Ł ß Æß | …ı Ł : |
(a) ˛Æ æ Ł æ Ł i Ł j (æ Œ ø… Ri ↔ Rj ),
(b) Ł æ i º Łæº r (æ Œ ø… Ri → rRi ), (c) ˙ æ i ª Ł æ Œ j (æ Œ ø… Ri →
Ri − rRj ),
º Œº æ Ł ŁŁ æłŁ Ø Ł ß æŁæ ß Œ Ł Ł Ø
, Ł … Œ, Æß Œ Ø æ Œ ß º ß º
Æߺ Ł Ł , Ł æ º ß Ł ß Ø Ł Ł Ø ÆߺŁ º Ł. ¨ Œ Ø Ł … Ø Ł Ł Ø ß æłŁ Ø Ł ß æŁæ ß º ªŒ º æ … ł Ł .
Łæ ŁØ æ æº Ø Ł Ø Œ æ æłŁ Ø Łæ
Œ Œ
1 = 38/ 7 x x 2 = −5/ 21 x 3 = 1/ 21 |
. | |||
| Ł Æ | Œ | Ł | ß | Œ d . |
Похожие работы
-
Лекции по математическому анализу
Определение функций нескольких переменных. Предел и непрерывность функции. Частные производные и полный дифференциал.
-
Геометрия 10 класс Бевз профиль
ШАНОВНІ СТАРШОКЛАСНИКИ! Ãåîìåòðіÿ – îäíà ç íàéäàâíіøèõ, íàéøëÿõåòíіøèõ, êîðèñíèõ і öіêàâèõ íàóê. Ó íіé – çãóñòîê çíà÷íîї ÷àñòèíè çàãàëüíîëþäñüêîї êóëüòóðè, íàäáàíîї ëþäñòâîì çà êіëüêà òèñÿ÷îëіòü. À ùå âîíà є íåçàìіííèì іíñòðóìåíòàðієì äëÿ íàóêîâöіâ і âèðîáíè÷íèêіâ, çàñîáîì äëÿ ðîçâèòêó ëîãі÷íîãî ìèñëåííÿ, ïðîñòîðîâîї óÿâè, ðàöіîíàëіçàòîðñüêèõ çäіáíîñòåé òà іíøèõ êîðèñíèõ ÿêîñòåé âîëі і õàðàêòåðó ìîëîäі.
-
Принятие решений в условиях риска 3
Федеральное агентство по образованию Новокузнецкий филиал – институт государственного образовательного учреждения высшего профессионального образования
-
Редуцированные полукольца
Основные понятия, леммы и предложения. Доказательство основной теоремы. Полукольцо отличается от ассоциативного кольца с единицей отсутствием операции вычитания. Основные трудности при работе с полукольцами.
-
Функция и ее свойства
Определение функции. Виды функций и их свойства.
-
Антье и ее окружение
Антье и ее свойства. Графики антье.
-
Три кризиса в развитии математики
РЕЦЕНЗИЯ на дипломную работу студента V курса физико-математического факультета АГПИ Большакова А. А. на тему: “Три кризиса в развитии математики”
-
Преобразования плоскости, движение
Преобразования плоскости Отображение плоскости на себя Отображенем плосости на себя называется такое преоброзование, что каждой точке исходной плоскости сопоставляется какая-то точка этой же плоскости, причем любая любая точка плоскости оказывается сопоставленой другой точке. Если при отображении плоскости на себя фигура F преобразовывается в фигуру F', то говорят, что фигура F' -
-
Метод релаксации переменных решения СЛАУ
Методы решения систем линейных уравнений. Метод Якоби в матричной записи. Достоинство итерационного метода верхних релаксаций, вычислительные погрешности. Метод блочной релаксации. Разбор метода релаксаций в системах линейных уравнений на примере.
-
Вероятностные процессы и математическая статистика в автоматизированных системах
Нахождение предела прочности алюминиевых деформируемых сплавов при испытании на растяжение. Расчет коэффициентов регрессии. Выбор и описание метода условной оптимизации. Результаты обработки данных эксперимента. Определение типа поверхности отклика.