Название: О реальной структуре электромагнитного поля и его характеристиках распространения в виде плоских волн.
Вид работы: статья
Рубрика: Физика
Размер файла: 106.6 Kb
Скачать файл: referat.me-340292.docx
Краткое описание работы: Системы полевых уравнений. Основная и отличительная особенность уравнений систем (2)-(4). Реальное электромагнитное поле. Волновой пакет плоской линейно поляризованной электрической волны. Реальное существование чисто магнитной поперечной волны.
О реальной структуре электромагнитного поля и его характеристиках распространения в виде плоских волн.
О РЕАЛЬНОЙ СТРУКТУРЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ И ЕГО ХАРАКТЕРИСТИКАХ РАСПРОСТРАНЕНИЯ В ВИДЕ ПЛОСКИХ ВОЛН
В.В. Сидоренков
МГТУ им. Н.Э. Баумана
Установлена реальная структура электромагнитного поля, представляющего собой векторное четырехкомпонентное электродинамическое поле, состоящего из функционально связанных между собой составляющих полей: электрической и магнитной напряженности, электрического и магнитного векторного потенциала. Рассматривается физически очевидный и принципиальный вопрос о параметрах и характеристиках распространения волн конкретных составляющих реального электромагнитного поля.
В настоящее время установлено, что в отношении полноты охвата при описании наблюдаемых в Природе явлений электромагнетизма, наряду с обычной системой уравнений электродинамики Максвелла электромагнитного
(ЭМ) поля
с компонентами электрической ![]() и магнитной
и магнитной ![]() напряженности [1]:
напряженности [1]:
(a) ![]() , (b)
, (b) ![]() , (1)
, (1)
(c)  , (d)
, (d) ![]() ,
,
существуют и другие системы полевых уравнений [2 - 4], концептуально необходимые при анализе и адекватном реальности физико-математическом моделировании электродинамических процессов в материальных средах. Уравнения в этих других системах рассматривают такие области пространства, где присутствуют либо только поле ЭМ векторного потенциала
с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a) ![]() , (b)
, (b) ![]() , (2)
, (2)
(c) 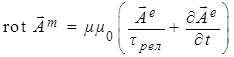 , (d)
, (d) ![]() ;
;
либо электрическое поле
с компонентами ![]() и
и ![]() :
:
(a) 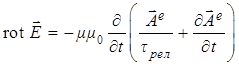 , (b)
, (b) ![]() , (3)
, (3)
(c) ![]() , (d)
, (d) ![]() ;
;
либо, наконец, магнитное поле
с компонентами ![]() и
и ![]() :
:
(a) 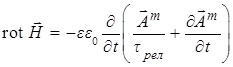 , (b)
, (b) ![]() , (4)
, (4)
(c) ![]() , (d)
, (d) ![]() .
.
Здесь ![]() и
и ![]() -
абсолютные диэлектрическая и магнитная проницаемости среды, соответственно,
-
абсолютные диэлектрическая и магнитная проницаемости среды, соответственно, ![]() - удельная электрическая проводимость,
- удельная электрическая проводимость, ![]() - постоянная времени релаксации заряда в среде за счет электропроводности.
- постоянная времени релаксации заряда в среде за счет электропроводности.
Основная и отличительная особенность уравнений систем (2) – (4) в сравнении с традиционными уравнениями Максвелла ЭМ поля (1) с физической точки зрения состоит в том, что именно они, используя представления о поле ЭМ векторного потенциала, способны последовательно описать многообразие электродинамических явлений нетепловой природы в материальных средах, определяемых электрической или магнитной поляризацией и передачей среде момента ЭМ импульса, в частности, реализуемых в процессе электрической проводимости [4, 5] .
Принципиально и весьма существенно здесь то, что все эти системы электродинамических уравнений, в частности, и система (1) для локально электронейтральных сред (![]() ) непосредственно следуют из фундаментальных исходных соотношений первичной взаимосвязи ЭМ поля и поля ЭМ векторного потенциала [2 - 4]:
) непосредственно следуют из фундаментальных исходных соотношений первичной взаимосвязи ЭМ поля и поля ЭМ векторного потенциала [2 - 4]:
(a) ![]() , (b)
, (b) ![]() , (5)
, (5)
(c) ![]() , (d)
, (d) 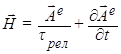 .
.
Очевидно, что представленная система соотношений может служить основой для интерпретации физического смысла поля ЭМ векторного потенциала [3], выяснения его роли и места в явлениях электромагнетизма. Однако самое главное и уникальное в них то, что все вместе эти соотношения являют собой систему базовых дифференциальных уравнений, описывающих необычное с точки зрения общепринятых позиций вихревое векторное поле, состоящее их четырех функционально связанных между собой вихревых векторных компонент ![]() ,
, ![]() ,
, ![]() и
и ![]() , которое условно назовем реальное электромагнитное поле
.
, которое условно назовем реальное электромагнитное поле
.
Объективность существования указанного поля однозначно иллюстрируется указанными системами уравнений (1) – (4) и получаемыми из них соотношениями баланса:
для потока ЭМ энергии из уравнений системы (1)
![]() , (6)
, (6)
для потока момента ЭМ импульса из уравнений системы (2)
div![]()
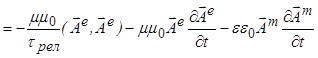 , (7)
, (7)
для потока электрической энергии из уравнений системы (3)
div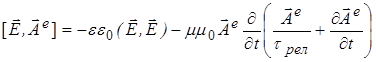 , (8)
, (8)
и, наконец, для потока магнитной энергии из уравнений системы (4)
div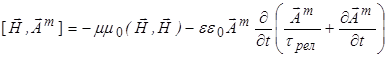 . . (9)
. . (9)
Как видим, соотношения (5) действительно следует считать фундаментальными уравнениями связи компонент реального электромагнитного поля
, базирующегося на исходной своей составляющей - поле векторного потенциала
, состоящего из двух взаимно ортогональных электрической ![]() и магнитной
и магнитной ![]() векторных полевых компонент. При этом поле векторного потенциала своим существованием реализует функционально связанные с ним другие составляющие единого поля: электромагнитное поле
с векторными компонентами
векторных полевых компонент. При этом поле векторного потенциала своим существованием реализует функционально связанные с ним другие составляющие единого поля: электромагнитное поле
с векторными компонентами ![]() и
и ![]() , электрическое поле
с компонентами
, электрическое поле
с компонентами ![]() и
и ![]() , магнитное поле
с компонентами
, магнитное поле
с компонентами ![]() и
и ![]() .
.
Интересно, что обсуждаемая здесь структура и взаимосвязь составляющих реального электромагнитного поля сохраняется и в статической асимптотике. Логика построения систем полевых уравнений для стационарных составляющих данного поля и анализ физического содержания таких уравнений изложены, например, в работе [6].
Форма представленных систем уравнений (1) – (4) говорит о существовании волновых решений для всех компонент ЭМ поля ![]() ,
, ![]() ,
, ![]() и
и ![]() . В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений любой системы, и после чего подставить в него другое роторное уравнение той же системы. Например, в качестве иллюстрации получим для системы (2) волновое уравнение относительно
. В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений любой системы, и после чего подставить в него другое роторное уравнение той же системы. Например, в качестве иллюстрации получим для системы (2) волновое уравнение относительно ![]() :
:
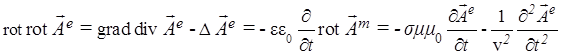 .
.
Здесь, согласно (2c), ![]() ,
, ![]() - оператор Лапласа, а
- оператор Лапласа, а ![]() - фазовая скорость поля волны в отсутствие поглощения. Следовательно, тем самым описываются волны для конкретной составляющей реального электромагнитного поля
посредством одной из парных комбинаций четырех указанных волновых уравнений. В итоге возникает физически очевидный вопрос, что это за волны, и каковы характеристики их распространения?
- фазовая скорость поля волны в отсутствие поглощения. Следовательно, тем самым описываются волны для конкретной составляющей реального электромагнитного поля
посредством одной из парных комбинаций четырех указанных волновых уравнений. В итоге возникает физически очевидный вопрос, что это за волны, и каковы характеристики их распространения?
В этой связи рассмотрим волновой пакет плоской линейно поляризованной, например, электрической волны,
распространяющейся вдоль оси 0X с компонентами ![]() и
и ![]() для системы (3) либо магнитной волны
с компонентами
для системы (3) либо магнитной волны
с компонентами ![]() и
и ![]() для системы (4), которые представим комплексными спектральными интегралами. Тогда, например, для уравнений электрического поля
(3) указанные интегралы имеют вид:
для системы (4), которые представим комплексными спектральными интегралами. Тогда, например, для уравнений электрического поля
(3) указанные интегралы имеют вид:
![]() и
и ![]() , (10)
, (10)
где ![]() и
и ![]() - комплексные амплитуды.
- комплексные амплитуды.
Подставляя их в уравнения (3a) и (3c), приходим к соотношениям 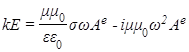 и
и ![]() . Соответствующая подстановка аналогичных (10) интегралов для магнитного поля
. Соответствующая подстановка аналогичных (10) интегралов для магнитного поля
![]() и
и ![]() в уравнения (4а) и (4c) дает
в уравнения (4а) и (4c) дает ![]() и
и ![]() . Таким образом, получаем для обеих систем общее для них выражение:
. Таким образом, получаем для обеих систем общее для них выражение: ![]()
В конкретном случае среды идеального диэлектрика (![]() ) с учетом формулы
) с учетом формулы ![]() для обеих систем из
для обеих систем из ![]() следует обычное дисперсионное соотношение
следует обычное дисперсионное соотношение ![]() [1], описывающее однородные плоские волны электрического или магнитного полей. При этом связь комплексных амплитуд компонент указанных волновых полей имеет специфический вид:
[1], описывающее однородные плоские волны электрического или магнитного полей. При этом связь комплексных амплитуд компонент указанных волновых полей имеет специфический вид:
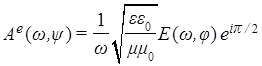 и
и 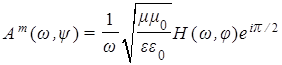 .
.
Специфика здесь в том, что при распространении в диэлектрической среде компоненты поля сдвинуты между собой по фазе на π/2. Конечно, математически данный результат тривиален, поскольку компоненты поля ЭМ напряженности и поля векторного потенциала связаны между собой посредством производной по времени (см. соотношения (5c) и (5d)). Однако концептуально с физической точки зрения это неожиданно и требует всестороннего анализа.
Справедливости ради следует сказать, что впервые о возможности реального существования чисто магнитной поперечной волны
с двумя ее компонентами ![]() и
и ![]() , сдвинутыми при распространении по фазе на π/2, официально в виде приоритета на открытие заявил Докторович еще в 1980 году, и этот факт он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других, ссылаясь на приоритет и свою статью по этой теме, везде публикуемую многие годы (например, [7]). Печально, но только Время - высший судья, и именно оно расставит всех и все по своим местам! Будем надеяться, что независимое подтверждение этого научного достижения Докторовича в представленном здесь исследовании будет для него серьезной поддержкой в общении с оппонентами.
, сдвинутыми при распространении по фазе на π/2, официально в виде приоритета на открытие заявил Докторович еще в 1980 году, и этот факт он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других, ссылаясь на приоритет и свою статью по этой теме, везде публикуемую многие годы (например, [7]). Печально, но только Время - высший судья, и именно оно расставит всех и все по своим местам! Будем надеяться, что независимое подтверждение этого научного достижения Докторовича в представленном здесь исследовании будет для него серьезной поддержкой в общении с оппонентами.
Соответствующие аналогичные вышеприведенным рассуждения теперь уже для ЭМ поля
с компонентами ![]() и
и ![]() системы (1) и для поля векторного потенциала
с компонентами
системы (1) и для поля векторного потенциала
с компонентами ![]() и
и ![]() системы (2) дают окончательно соотношения
системы (2) дают окончательно соотношения ![]() ,
, ![]() и
и ![]() ,
, 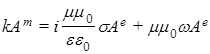 . В итоге для этих двух систем уравнений снова получаем стандартное выражение:
. В итоге для этих двух систем уравнений снова получаем стандартное выражение: ![]()
Для диэлектрической среды
(![]() ) дисперсионное соотношение для волновых решений уравнений систем (1) и (2) также будет обычное
) дисперсионное соотношение для волновых решений уравнений систем (1) и (2) также будет обычное ![]() , что описывает режим распространения компонент поля ЭМ напряженности и поля векторного потенциала в виде однородных плоских волн. При этом связь комплексных амплитуд решений системы (1) имеет стандартный вид
, что описывает режим распространения компонент поля ЭМ напряженности и поля векторного потенциала в виде однородных плоских волн. При этом связь комплексных амплитуд решений системы (1) имеет стандартный вид 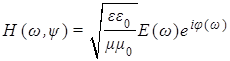 [1] и
[1] и 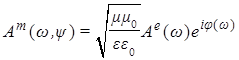 для системы (2), а сами волновые решения описывают волны, компоненты поля которых синфазно распространяются в пространстве. Причем, согласно соотношениям (5c) и (5d), волны поля ЭМ напряженности сдвинуты по фазе на π/2 от волн векторного потенциала, что и приводит к вышеуказанной определенной специфике в поведении компонент полей электрической и магнитной волн.
для системы (2), а сами волновые решения описывают волны, компоненты поля которых синфазно распространяются в пространстве. Причем, согласно соотношениям (5c) и (5d), волны поля ЭМ напряженности сдвинуты по фазе на π/2 от волн векторного потенциала, что и приводит к вышеуказанной определенной специфике в поведении компонент полей электрической и магнитной волн.
Легко убедиться, что для проводящей среды (![]() ) в асимптотике металлов (
) в асимптотике металлов (![]() ) дисперсионное соотношение для всех систем уравнений имеет обычный в таком случае вид
) дисперсионное соотношение для всех систем уравнений имеет обычный в таком случае вид ![]() [1], где
[1], где ![]() . Тогда связи комплексных амплитуд запишутся для систем (3) и (4) как
. Тогда связи комплексных амплитуд запишутся для систем (3) и (4) как 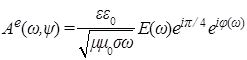 и
и 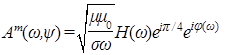 , а для (1) и (2)
, а для (1) и (2)  и
и 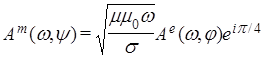 .
.
Как видим, в данном случае распространение волн всех четырех составляющих реального электромагнитного поля подчиняется теоретически хорошо изученному закону для плоских волн ЭМ поля в металлах [1], когда волновые решения для проводящей среды имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на π/4.
Таким образом, как представляется, нам удалось провести серьезную концептуальную модернизацию основных воззрений о структуре и свойствах электромагнитного поля в классической электродинамике, где, в частности, показано, что, в Природе нет электрического, магнитного или другой составляющей реального электромагнитного поля с одной полевой компонентой. Структурно эти четыре составляющие принципиально состоят из двух векторных взаимно ортогональных полевых компонент, благодаря которым для конкретной составляющей реализуется объективно необходимый способ ее существования, принципиальная и единственная возможность распространения в виде потока соответствующей физической величины, в случае динамических полей - посредством поперечных волн.
Обобщая полученные результаты, приходим к выводу о том, что совокупность полей, определяемая соотношениями (5), действительно является четырехкомпонентным векторным электромагнитным полем , распространяющимся в пространстве в виде единого волнового процесса, а потому с концептуальной точки зрения разделение реального электромагнитного поля на составляющие его поля в определенной мере условно. Однако с позиций общепринятых физических представлений и практики аналитического описания явлений электромагнетизма разделение этого поля на двухкомпонентные составляющие в виде электрического, магнитного, электромагнитного и векторного потенциала полей однозначно необходимо и, безусловно, удобно, поскольку диктуется объективным существованием конкретных электромагнитных явлений и процессов, реализуемых посредством рассматриваемых двухкомпонентных составляющих. Кстати, по поводу предложенного названия обсуждаемого здесь электродинамического поля. По нашему мнению, очевидно, что серьезных проблем не должно возникнуть, если в перспективе обсуждаемое поле сохранит за собой и традиционное нынешнее название – электромагнитное поле .
Литература:
1. Матвеев А.Н. Электродинамика. М.: Высшая школа, 1980. 383 с.
2. Сидоренков В.В. Обобщение физических представлений о векторных потенциалах в классической электродинамике // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2006. № 1. С. 28-37.
3. Сидоренков В.В. Физические основы теории поля векторных потенциалов в классической электродинамике // Материалы IX Международной конференции «Физика в системе современного образования». Санкт-Петербург: РГПУ, 2007. Т. 1. Секция “Профессиональное физическое образование”. С. 127-129.
4. Сидоренков В.В. Фундаментальные основы электродинамической теории нетеплового действия электромагнитных полей на материальные среды // Вестник Воронежского государственного технического университета. 2007. Т.3. № 11. С.75-82.
5. Сидоренков В.В. Развитие физических представлений о процессе электрической проводимости в металлах // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2005. № 2. С. 35-46.
6. Сидоренков В.В. Гипотетическое построение уравнений теории поля стационарных электромагнитных явлений // XLIV Всероссийская конференция по проблемам математики, информатики, физики и химии: Тезисы докладов. Секция «Теоретическая физика». М.: РУДН, 2008. С. 96-97.
7. Докторович З.И. Несостоятельность теории электромагнетизма и выход из сложившегося тупика // http ://www.sciteclibrary.ru/rus/catalog/pages/4797.html .
Похожие работы
-
Билеты по Физике
Вопросы к экзамену по Физике Электрический ток в электролитах. Законы электролиза. Электропроводимость газов. Самостоятельный и несамостоятельный газовые разряды.
-
Новые реалии в физическом содержании великих уравнений электродинамики Максвелла
На основе анализа традиционных электродинамических уравнений Максвелла выявлены принципиально новые реалии в их физическом содержании. Модернизация концептуальных представлений классической электродинамики о структуре и свойствах электромагнитного поля.
-
Уравнения и характеристики распространения волн реального электромагнитного поля
Уравнения, структура и параметры реального электромагнитного поля, состоящего из функционально связанных между собой четырех полевых векторных компонент: электрической и магнитной напряженностей, электрического и магнитного векторного потенциала.
-
Изучение плоских диэлектрических волноводов для ТЕ поляризации
Переменное электромагнитное поле в однородной среде или вакууме. Формулы Френеля. Угол Брюстера. Уравнения, описывающие распространение электромагнитных волн в плоском оптическом волноводе. Дисперсионные уравнения трехслойного диэлектрического волновода.
-
Магнитные и электромагнитные поле
Магнитные и электромагнитные поле. Электрическое и магнитные поля тесно связаны между собой. В природе существует электромагнитное поле - чисто электрические и чисто магнитные поля являются лишь его частными случаями. Изменяющиеся электрические и магнитные поля индуктируют друг друга.(под изменением поля надо понимать не только изменение его интенсивности, но и движение поля как целого).
-
Электронные цепи СВЧ (конспект) Add1
Параметры матрицы рассеяния могут быть рассчитаны по известной матрице проводимости четырехполюсника по формуле: – единичная матрица. Необходимо отметить важную особенность параметров матрицы рассеяния, связанную с направлением прохождения сигнала. При изменении направления передачи изменятся лишь индексы в параметрах рассеяния (
-
Экспериментальное наблюдение волн магнитного поля и исследование их распространения в металлах
В.В. Сидоренков МГТУ им. Н.Э. Баумана В настоящее время установлено [1], что реальная структура электромагнитного (ЭМ) поля представляет собой необычное с общепринятых позиций вихревое векторное поле, состоящее из двух функционально связанных между собой электродинамических полей: вихревог ЭМ поля с компонентами электрической
-
СВЧ элементы
Узбекское агентство связи и информатизации Ташкентский университет информационных технологий Кафедра антенно-фидерных устройств РАБОЧАЯ ПРОГРАММА
-
Электромагнитные волны между параллельными идеально проводящими плоскостями
КОНТРОЛЬНАЯ РАБОТА ПО ЭЛЕКТРОДИНАМИКЕ: «Электромагнитные волны между параллельными идеально проводящими плоскостями» Введение На больших расстояниях от антенны электромагнитное поле имеет характер сферической волны. При движении такой волны в точку, где находится потребитель энергии (приемное устройство), естественно, попадает лишь незначительная часть общей энергии, излучаемой антенной.
-
О парадоксе существования волн электромагнитного поля и их способности переноса полевой энергии
Концептуальное развитие основных физических воззрений на структуру и свойства электромагнитного поля в классической электродинамике. Системы полевых уравнений. Волновой пакет плоской линейно поляризованной электрической волны. Электромагнитные поля.