Название: Расчет электрической цепи

Вид работы: контрольная работа

Рубрика: Физика

Размер файла: 244.01 Kb

Скачать файл: referat.me-340705.docx

Краткое описание работы: Расчет линейной электрической цепи при периодическом несинусоидальном напряжении, активной и полной мощности сети. Порядок определения параметров несимметричной трехфазной цепи. Вычисление основных переходных процессов в линейных электрических цепях.

Расчет электрической цепи

1. Расчет линейной электрической цепи при периодическом несинусоидальном напряжении

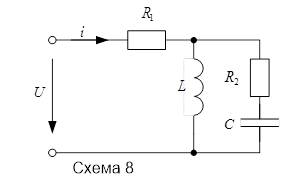
Задание 6		Приложенное несинусоидальное напряжение описано выражением:

Решение

Найти действующее напряжение .

;

;;

Приложенное несинусоидальное напряжение будет описано рядом:

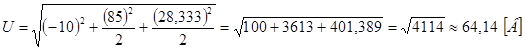
Действующее напряжение .

Вычислить сопротивления цепи ,, и токи ,, на неразветвленном участке цепи от действия каждой гармоники приложенного напряжения.

Сопротивление цепи постоянному току (w = 0)

Постоянная составляющая тока на неразветвленном участке цепи

Сопротивление цепи на частоте w (для первой гармоники)

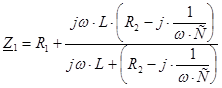
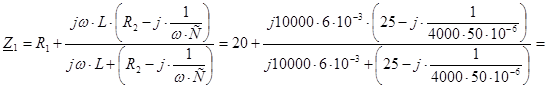
Комплексная амплитуда тока первой гармоники на неразветвленном участке цепи

;

Ток первой гармоники на неразветвленном участке цепи

.

Сопротивление цепи на частоте 3w (для третьей гармоники)

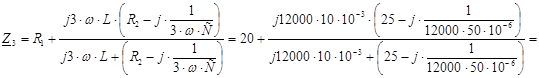
Комплексная амплитуда тока третьей гармоники на неразветвленном участке цепи

; .

Ток третьей гармоники на неразветвленном участке цепи

.

Определить мгновенный ток на неразветвленном участке и действующий ток .

Ток на неразветвленном участке цепи

;

.

Действующее значение тока на неразветвленном участке цепи

;

.

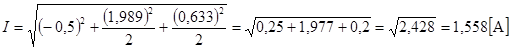Рассчитать активную и полную мощности цепи.

Активная мощность цепи

;

; ; ,

гдеb₁ , b₃ , b₅ – начальные фазы гармоник напряжения;

a₁ , a₃ , a₅ – начальные фазы гармоник тока.

Полная мощность цепи

; .

Построить кривые , .

Периодическая несинусоидальная ЭДС и ее представление тремя гармониками.

2. Расчет не симметричной трехфазной цепи

Дана схема 8

Задание 6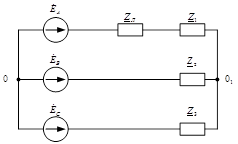

Решение

Для симметричного источника, соединенного звездой, при ЭДС фазы А

ЭДС фаз В и С:;

.

Расчетная схема содержит два узла – и . Принимая потенциал узла , в соответствии с методом узловых потенциалов получим:

,

где ;

;

;

;

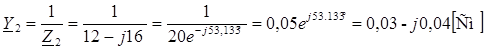Так как: .

То с учетом приведенных обозначений потенциал в точке

.

Тогда смещение напряжения относительно нейтрали источника N

Линейные токи:

Составить баланс мощностей

Комплексная мощность источника

;

Активная мощность цепи равна суммарной мощности потерь в резисторах:

.

Реактивная мощность цепи

.

Видно, что баланс мощностей сошелся:

.

.

Напряжения на фазах нагрузки:

;

;

;

;

Токи:

Построить в масштабе векторную диаграмму токов и потенциальную топографическую диаграмму напряжений,

,.

,,,

,

,,

Все вектора строятся на комплексной координатной плоскости.

Можно сначала построить вектора напряжений в ветвях, а потом провести вектор из начала координат в точку, в которой сойдутся напряжения ветвей, этот вектор должен соответствовать вектору напряжения смещения нормали. Проводим вектор так, чтоб он заканчивался в конце вектора , проводим вектор так, чтоб он заканчивался в конце вектора . Проводим вектор так, чтоб он заканчивался в конце вектора . Проводим вектор так, чтоб он заканчивался в конце вектора .

Векторы ,,, начинаются из одной точки.

Проведем из этой точки вектор в начало координат и у нас получится вектор напряжение смещения нейтрали . Вектора токов строим из начала координат.

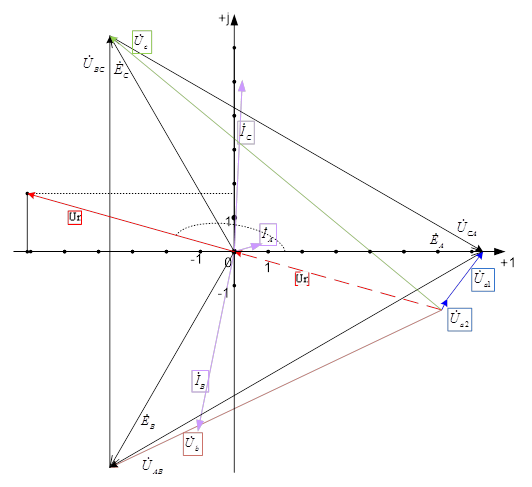
По диаграмме можно определить напряжение нейтрали:

или

3. Расчет переходных процессов в линейных электрических цепях с сосредоточенными параметрами, включенных на постоянное напряжение

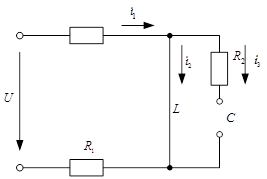
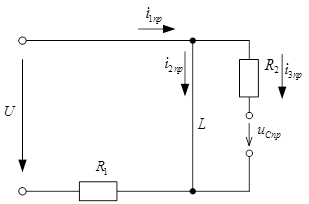
Дана схема

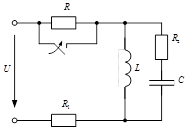Решение

1. Установившийся режим до коммутации. Имеет место установившийся режим постоянных токов

; ;

;

При t = 0–

, .

Дифференциальные уравнения описывают токи и напряжения с момента времени t = 0+.

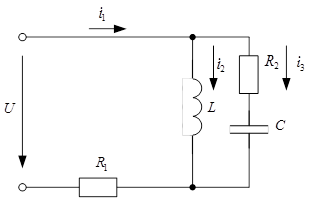
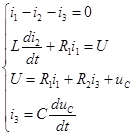
Принужденные составляющие находятся для установившегося режима, наступающего после переходного процесса.

Определение корней характеристического уравнения. Входное комплексное сопротивление переменному току схемы для послекоммутационного состояния.

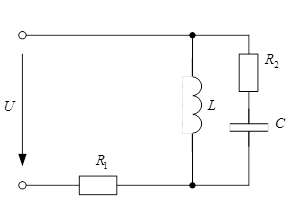
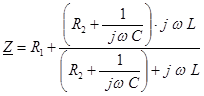
Заменяя далее j w на р и приравнивая полученный результат к нулю, получаем

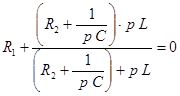
Характеристическое уравнение имеет корни:

,

Следовательно, имеет место апериодический переходный режим.

Определение постоянных. В результате расчета получены следующие выражения для неизвестных:

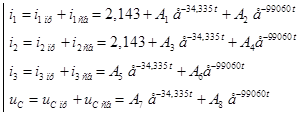
На этом этапе система диф. уравнений записывается для момента времени t = 0+ и после подстановки параметров с учетом равенств

получаем:

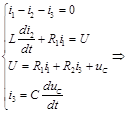
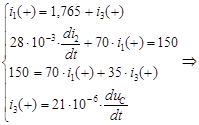
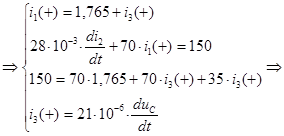
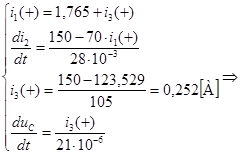
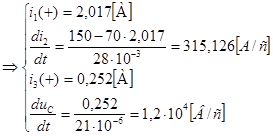
Решение системы дает:

, ,,

Для нахождения и продифференцируем первое и третье уравнения системы, запишем их при t = 0+ и подставим известные величины:

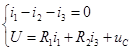
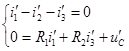
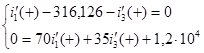
Затем выражения для тока в индуктивности и напряжения на емкости и их производные записываются для момента времени t = 0+:

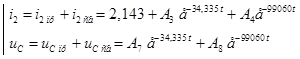
После подстановки получим:

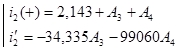
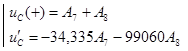
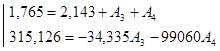
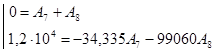
Решение систем:

,

,

Получим:

Для построения графиков возьмем шаг: .

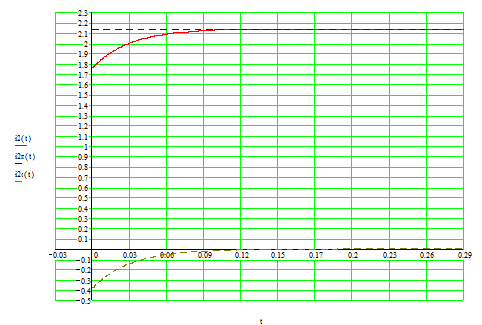
Изобразим график функции напряжения на конденсаторе:

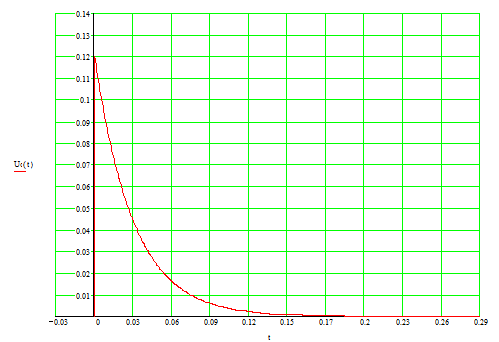
Из системы диф. уравнений:

Изобразим график функции первого тока:

Из системы диф. уравнений:

– первое уравнение.

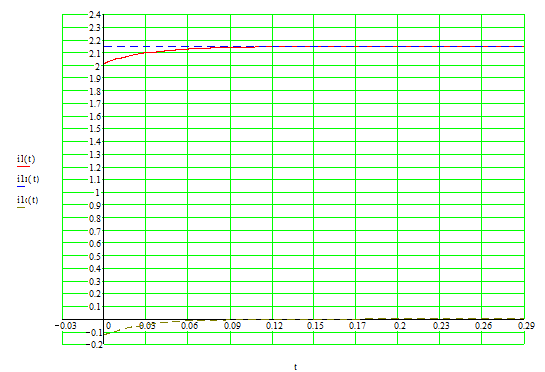
Изобразим график функции третьего тока:

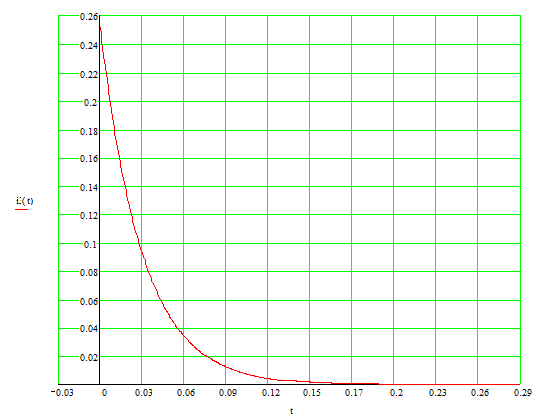
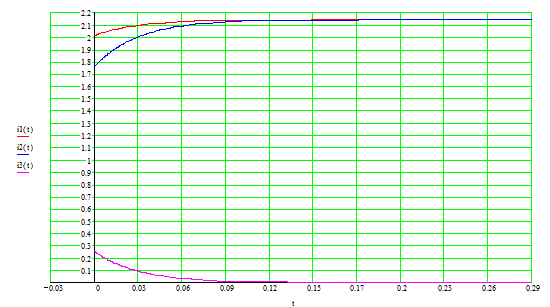
Нанесем все токи на одну координатную плоскость:

,

,